Rotate a matrix by 90 degree in clockwise direction without using any extra space

Given a square matrix, turn it by 90 degrees in a clockwise direction without using any extra space.

Examples:

Input:
1 2 3 
4 5 6
7 8 9  
Output:
7 4 1 
8 5 2
9 6 3

Input:
1 2
3 4
Output:
3 1
4 2 

Method 1

Approach: The approach is similar to Inplace rotate square matrix by 90 degrees | Set 1. The only thing that is different is to print the elements of the cycle in a clockwise direction i.e. An N x N matrix will have floor(N/2) square cycles. 
For example, a 3 X 3 matrix will have 1 cycle. The cycle is formed by its 1st row, last column, last row, and 1st column. 
For each square cycle, we swap the elements involved with the corresponding cell in the matrix in the clockwise direction. We just need a temporary variable for this.

Explanation:

Let size of row and column be 3. 
During first iteration –
a[i][j] = Element at first index (leftmost corner top)= 1.
a[j][n-1-i]= Rightmost corner top Element = 3.
a[n-1-i][n-1-j] = Rightmost corner bottom element = 9.
a[n-1-j][i] = Leftmost corner bottom element = 7.
Move these elements in the clockwise direction. 
During second iteration –
a[i][j] = 2.
a[j][n-1-i] = 6.
a[n-1-i][n-1-j] = 8.
a[n-1-j][i] = 4. 
Similarly, move these elements in the clockwise direction. 

Below is the implementation of the above approach: 

C++

// C++ implementation of above approach
#include <bits/stdc++.h>
using namespace std;

#define N 4

// Function to rotate the matrix 90 degree clockwise
void rotate90Clockwise(int a[N][N])
{

    // Traverse each cycle
    for (int i = 0; i < N / 2; i++) {
        for (int j = i; j < N - i - 1; j++) {

            // Swap elements of each cycle
            // in clockwise direction
            int temp = a[i][j];
            a[i][j] = a[N - 1 - j][i];
            a[N - 1 - j][i] = a[N - 1 - i][N - 1 - j];
            a[N - 1 - i][N - 1 - j] = a[j][N - 1 - i];
            a[j][N - 1 - i] = temp;
        }
    }
}

// Function for print matrix
void printMatrix(int arr[N][N])
{
    for (int i = 0; i < N; i++) {
        for (int j = 0; j < N; j++)
            cout << arr[i][j] << " ";
        cout << '\n';
    }
}

// Driver code
int main()
{
    int arr[N][N] = { { 1, 2, 3, 4 },
                      { 5, 6, 7, 8 },
                      { 9, 10, 11, 12 },
                      { 13, 14, 15, 16 } };
    rotate90Clockwise(arr);
    printMatrix(arr);
    return 0;
}

Java

// Java implementation of above approach
import java.io.*;

class GFG
{

static int N = 4;

// Function to rotate the matrix 90 degree clockwise
static void rotate90Clockwise(int a[][])
{

    // Traverse each cycle
    for (int i = 0; i < N / 2; i++)
    {
        for (int j = i; j < N - i - 1; j++)
        {

            // Swap elements of each cycle
            // in clockwise direction
            int temp = a[i][j];
            a[i][j] = a[N - 1 - j][i];
            a[N - 1 - j][i] = a[N - 1 - i][N - 1 - j];
            a[N - 1 - i][N - 1 - j] = a[j][N - 1 - i];
            a[j][N - 1 - i] = temp;
        }
    }
}

// Function for print matrix
static void printMatrix(int arr[][])
{
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        System.out.print( arr[i][j] + " ");
        System.out.println();
    }
}

// Driver code

    public static void main (String[] args)
    {
            int arr[][] = { { 1, 2, 3, 4 },
                      { 5, 6, 7, 8 },
                      { 9, 10, 11, 12 },
                      { 13, 14, 15, 16 } };
    rotate90Clockwise(arr);
    printMatrix(arr);
    }
}

// This code has been contributed by inder_verma.

Python

# Function to rotate the matrix
# 90 degree clockwise
def rotate90Clockwise(A):
    N = len(A[0])
    for i in range(N // 2):
        for j in range(i, N - i - 1):
            temp = A[i][j]
            A[i][j] = A[N - 1 - j][i]
            A[N - 1 - j][i] = A[N - 1 - i][N - 1 - j]
            A[N - 1 - i][N - 1 - j] = A[j][N - 1 - i]
            A[j][N - 1 - i] = temp

# Function to print the matrix
def printMatrix(A):
    N = len(A[0])
    for i in range(N):
        print(A[i])

# Driver code
A = [[1, 2, 3, 4],
     [5, 6, 7, 8],
     [9, 10, 11, 12],
     [13, 14, 15, 16]]
rotate90Clockwise(A)
printMatrix(A)

# This code was contributed
# by pk_tautolo

C#

// C# implementation of above approach
using System;

class GFG
{
static int N = 4;

// Function to rotate the matrix
// 90 degree clockwise
static void rotate90Clockwise(int[,] a)
{

    // Traverse each cycle
    for (int i = 0; i < N / 2; i++)
    {
        for (int j = i; j < N - i - 1; j++)
        {

            // Swap elements of each cycle
            // in clockwise direction
            int temp = a[i, j];
            a[i, j] = a[N - 1 - j, i];
            a[N - 1 - j, i] = a[N - 1 - i, N - 1 - j];
            a[N - 1 - i, N - 1 - j] = a[j, N - 1 - i];
            a[j, N - 1 - i] = temp;
        }
    }
}

// Function for print matrix
static void printMatrix(int[,] arr)
{
    for (int i = 0; i < N; i++)
    {
        for (int j = 0; j < N; j++)
        Console.Write( arr[i, j] + " ");
        Console.Write("\n");
    }
}

// Driver code
public static void Main ()
    {
    int [,]arr = {{1, 2, 3, 4},
                  {5, 6, 7, 8},
                  {9, 10, 11, 12},
                  {13, 14, 15, 16}};
    rotate90Clockwise(arr);
    printMatrix(arr);
}
}

// This code is contributed
// by ChitraNayal

PHP

<?php
// PHP implementation of above approach
$N = 4;

// Function to rotate the matrix
// 90 degree clockwise
function rotate90Clockwise(&$a)
{
    global $N;

    // Traverse each cycle
    for ($i = 0; $i < $N / 2; $i++)
    {
        for ($j = $i;
             $j < $N - $i - 1; $j++)
        {

            // Swap elements of each cycle
            // in clockwise direction
            $temp = $a[$i][$j];
            $a[$i][$j] = $a[$N - 1 - $j][$i];
            $a[$N - 1 - $j][$i] =
               $a[$N - 1 - $i][$N - 1 - $j];
            $a[$N - 1 - $i][$N - 1 - $j] =
                         $a[$j][$N - 1 - $i];
            $a[$j][$N - 1 - $i] = $temp;
        }
    }
}

// Function for print matrix
function printMatrix(&$arr)
{
    global $N;
    for ($i = 0; $i < $N; $i++)
    {
        for ($j = 0; $j < $N; $j++)
            echo $arr[$i][$j] . " ";
        echo "\n";
    }
}

// Driver code
$arr = array(array(1, 2, 3, 4),
             array(5, 6, 7, 8),
             array(9, 10, 11, 12),
             array(13, 14, 15, 16));
rotate90Clockwise($arr);
printMatrix($arr);

// This code is contributed
// by ChitraNayal
?>

Javascript

<script>

// Javascript implementation of above approach

    var N = 4;

    // Function to rotate the matrix 90 degree clockwise
    function rotate90Clockwise(a) {

        // Traverse each cycle
        for (i = 0; i < parseInt(N / 2); i++) {
            for (j = i; j < N - i - 1; j++) {

                // Swap elements of each cycle
                // in clockwise direction
                var temp = a[i][j];
                a[i][j] = a[N - 1 - j][i];
                a[N - 1 - j][i] = a[N - 1 - i][N - 1 - j];
                a[N - 1 - i][N - 1 - j] = a[j][N - 1 - i];
                a[j][N - 1 - i] = temp;
            }
        }
    }

    // Function for print matrix
    function printMatrix(arr) {
        for (i = 0; i < N; i++) {
            for (j = 0; j < N; j++)
                document.write(arr[i][j] + " ");
            document.write("<br/>");
        }
    }

    // Driver code


        var arr = [ [ 1, 2, 3, 4 ],
                    [ 5, 6, 7, 8 ],
                    [ 9, 10, 11, 12 ],
                    [ 13, 14, 15, 16 ] ];
        rotate90Clockwise(arr);
        printMatrix(arr);

// This code contributed by Rajput-Ji

</script>

Output

13 9 5 1 
14 10 6 2 
15 11 7 3 
16 12 8 4 

Complexity Analysis:

Time Complexity – O(n*n)

Auxiliary Space – O(1)

Method 2:

Approach: The approach is based on the pattern made by indices after rotating the matrix. Consider the following illustration to have a clear insight into it.

Consider a 3 x 3 matrix having indices (i, j) as follows. 

00 01 02 
10 11 12 
20 21 22

After rotating the matrix by 90 degrees in clockwise direction, indices transform into
20 10 00  current_row_index = 0, i = 2, 1, 0 
21 11 01 current_row_index = 1, i = 2, 1, 0 
22 12 02  current_row_index = 2, i = 2, 1, 0

Observation: In any row, for every decreasing row index i, there exists a constant column index j, such that j = current_row_index. 

This pattern can be printed using 2 nested loops.
(This pattern of writing indices is achieved by writing the exact indices of the desired elements of 
where they actually existed in the original array.)  

Below is the implementation of the above approach:

C++

// C++ implementation of above approach
#include <bits/stdc++.h>
using namespace std;

#define N 4

// Function to rotate the matrix 90 degree clockwise
void rotate90Clockwise(int arr[N][N])
{
    // printing the matrix on the basis of
    // observations made on indices.
    for (int j = 0; j < N; j++)
    {
        for (int i = N - 1; i >= 0; i--)
            cout << arr[i][j] << " ";
        cout << '\n';
    }
}

// Driver code
int main()
{
    int arr[N][N] = { { 1, 2, 3, 4 },
                      { 5, 6, 7, 8 },
                      { 9, 10, 11, 12 },
                      { 13, 14, 15, 16 } };
    rotate90Clockwise(arr);
    return 0;
}

// This code is contributed by yashbeersingh42

Java

// Java implementation of above approach
import java.io.*;

class GFG {
    static int N = 4;

    // Function to rotate the matrix 90 degree clockwise
    static void rotate90Clockwise(int arr[][])
    {
        // printing the matrix on the basis of
        // observations made on indices.
        for (int j = 0; j < N; j++)
        {
            for (int i = N - 1; i >= 0; i--)
                System.out.print(arr[i][j] + " ");
            System.out.println();
        }
    }
    public static void main(String[] args)
    {
        int arr[][] = { { 1, 2, 3, 4 },
                        { 5, 6, 7, 8 },
                        { 9, 10, 11, 12 },
                        { 13, 14, 15, 16 } };
        rotate90Clockwise(arr);
    }
}
// This code is contributed by yashbeersingh42

Python3

# Python3 implementation of above approach
N = 4

# Function to rotate the matrix 90 degree clockwise
def rotate90Clockwise(arr) :
    global N

    # printing the matrix on the basis of
    # observations made on indices.
    for j in range(N) :
        for i in range(N - 1, -1, -1) :
            print(arr[i][j], end = " ")
        print()

# Driver code
arr = [ [ 1, 2, 3, 4 ],
          [ 5, 6, 7, 8 ],
          [ 9, 10, 11, 12 ],
          [ 13, 14, 15, 16 ] ]
rotate90Clockwise(arr);

# This code is contributed by divyesh072019.

C#

// C# implementation of above approach
using System;
class GFG {

    static int N = 4;

    // Function to rotate the matrix 90 degree clockwise
    static void rotate90Clockwise(int[,] arr)
    {

        // printing the matrix on the basis of
        // observations made on indices.
        for (int j = 0; j < N; j++)
        {
            for (int i = N - 1; i >= 0; i--)
                Console.Write(arr[i, j] + " ");
            Console.WriteLine();
        }
    }

  // Driver code
  static void Main() {
    int[,] arr = { { 1, 2, 3, 4 },
                  { 5, 6, 7, 8 },
                  { 9, 10, 11, 12 },
                  { 13, 14, 15, 16 } };
    rotate90Clockwise(arr);
  }
}

// This code is contributed by divyeshrabadiya07.

Javascript

<script>
// javascript implementation of above approach
    var N = 4;

    // Function to rotate the matrix 90 degree clockwise
    function rotate90Clockwise(arr) {
        // printing the matrix on the basis of
        // observations made on indices.
        for (j = 0; j < N; j++) {
            for (i = N - 1; i >= 0; i--)
                document.write(arr[i][j] + " ");
            document.write("<br/>");
        }
    }


        var arr = [ [ 1, 2, 3, 4 ],
                    [ 5, 6, 7, 8 ],
                    [ 9, 10, 11, 12 ],
                    [ 13, 14, 15, 16 ] ];
        rotate90Clockwise(arr);

// This code contributed by Rajput-Ji
</script>

Output

13 9 5 1 
14 10 6 2 
15 11 7 3 
16 12 8 4 

Complexity Analysis:

Time Complexity – O(n*n)

Auxiliary Space – O(1)

Method 3:

 Approach: The Approach is to rotate the given matrix two times, first time with respect to the Main diagonal, next time rotate the resultant matrix with respect to the middle column, Consider the following illustration to have a clear insight into it.

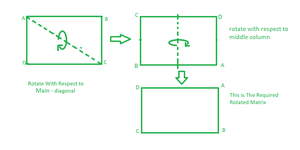
 Rotate square matrix 90 degrees in a clockwise direction

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>
using namespace std;

#define N 4

void print(int arr[N][N])
{
    for(int i = 0; i < N; ++i)
    {
        for(int j = 0; j < N; ++j)
            cout << arr[i][j] << " ";

        cout << '\n';
    }
}

void rotate(int arr[N][N])
{

    // First rotation
    // with respect to main diagonal
    for(int i = 0; i < N; ++i)
    {
        for(int j = 0; j < i; ++j)
        {
            int temp = arr[i][j];
            arr[i][j] = arr[j][i];
            arr[j][i] = temp;
        }
    }

    // Second rotation
    // with respect to middle column
    for(int i = 0; i < N; ++i)
    {
        for(int j = 0; j < N / 2; ++j)
        {
            int temp = arr[i][j];
            arr[i][j] = arr[i][N - j - 1];
            arr[i][N - j - 1] = temp;
        }
    }
}

// Driver code
int main()
{
    int arr[N][N] = { { 1, 2, 3, 4 },
                      { 5, 6, 7, 8 },
                      { 9, 10, 11, 12 },
                      { 13, 14, 15, 16 } };
    rotate(arr);
    print(arr);
    return 0;
}

// This code is contributed  by Rahul Verma

Java

import java.io.*;

class GFG {

  static void rotate(int[][] arr) {

        int n=arr.length;

    // first rotation
    // with respect to main diagonal
        for(int i=0;i<n;++i)
        {
            for(int j=0;j<i;++j)
            {
                int temp = arr[i][j];
                arr[i][j]=arr[j][i];
                arr[j][i]=temp;
            }
        }
         // Second rotation
    // with respect to middle column
        for(int i=0;i<n;++i)
        {
            for(int j=0;j<n/2;++j)
            {
                int temp =arr[i][j];
                arr[i][j] = arr[i][n-j-1];
                arr[i][n-j-1]=temp;
            }
        }

    }

  // to print matrix
   static void printMatrix(int arr[][])
    {
        int n=arr.length;
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n; j++)
                System.out.print( arr[i][j] + " ");
            System.out.println();
        }
    }
  // Driver code
    public static void main (String[] args) {
       int arr[][] = { { 1, 2, 3, 4 },
                      { 5, 6, 7, 8 },
                      { 9, 10, 11, 12 },
                      { 13, 14, 15, 16 } };
    rotate(arr);
    printMatrix(arr);
    }
}
// This code is contributed  by Rahul Verma

Python3

# Python3 implementation of above approach
N = 4

# Function to rotate the matrix 90 degree clockwise
def rotate(arr):
    global N

    # First rotation
# with respect to main diagonal
    for i in range(N):
        for j in range(i):
            temp = arr[i][j]
            arr[i][j] = arr[j][i]
            arr[j][i] = temp

    # Second rotation
# with respect to middle column
    for i in range(N):
        for j in range(int(N/2)):
            temp = arr[i][j]
            arr[i][j] = arr[i][N-j-1]
            arr[i][N-j-1] = temp


# Driver code
arr = [[1, 2, 3, 4],
       [5, 6, 7, 8],
       [9, 10, 11, 12],
       [13, 14, 15, 16]]

rotate(arr)

for i in range(N):
    for j in range(N):
        print(arr[i][j], end=" ")
    print()

# This code is contributed by Aarti_Rathi

C#

using System;
using System.Collections.Generic;
public class GFG {

  static void rotate(int[,] arr) {

        int n=arr.GetLength(0);

    // first rotation
    // with respect to main diagonal
        for(int i=0;i<n;++i)
        {
            for(int j=0;j<i;++j)
            {
                int temp = arr[i,j];
                arr[i,j]=arr[j,i];
                arr[j,i]=temp;
            }
        }
         // Second rotation
    // with respect to middle column
        for(int i=0;i<n;++i)
        {
            for(int j=0;j<n/2;++j)
            {
                int temp =arr[i,j];
                arr[i,j] = arr[i,n-j-1];
                arr[i,n-j-1]=temp;
            }
        }

    }

  // to print matrix
   static void printMatrix(int [,]arr)
    {
        int n=arr.GetLength(0);
        for (int i = 0; i < n; i++)
        {
            for (int j = 0; j < n; j++)
                Console.Write( arr[i,j] + " ");
            Console.WriteLine();
        }
    }
  // Driver code
    public static void Main(String[] args) {
       int [,]arr = { { 1, 2, 3, 4 },
                      { 5, 6, 7, 8 },
                      { 9, 10, 11, 12 },
                      { 13, 14, 15, 16 } };
    rotate(arr);
    printMatrix(arr);
    }
}

// This code contributed by Rajput-Ji

Javascript

<script>

let N = 4

function print(arr)
{
    for(let i = 0; i < N; ++i)
    {
        for(let j = 0; j < N; ++j)
            document.write(arr[i][j] + " ");

        document.write("<br>");
    }
}

function rotate(arr)
{

    // First rotation
    // with respect to main diagonal
    for(let i = 0; i < N; ++i)
    {
        for(let j = 0; j < i; ++j)
        {
            let temp = arr[i][j];
            arr[i][j] = arr[j][i];
            arr[j][i] = temp;
        }
    }

    // Second rotation
    // with respect to middle column
    for(let i = 0; i < N; ++i)
    {
        for(let j = 0; j < N / 2; ++j)
        {
            let temp = arr[i][j];
            arr[i][j] = arr[i][N - j - 1];
            arr[i][N - j - 1] = temp;
        }
    }
}

// Driver code

    let arr = [ [ 1, 2, 3, 4 ],
                    [ 5, 6, 7, 8 ],
                    [ 9, 10, 11, 12 ],
                    [ 13, 14, 15, 16 ] ];
    rotate(arr);
    print(arr);

//This code is contributed by Mayank Tyagi
</script>

Output

13 9 5 1 
14 10 6 2 
15 11 7 3 
16 12 8 4 

Complexity Analysis:

Time Complexity – O(n*n)

Auxiliary Space – O(1)

Method 4:

Approach: This approach is similar to method 3 the only difference is that in first rotation we rotate about the Secondary Diagonal and after that about the Middle row.

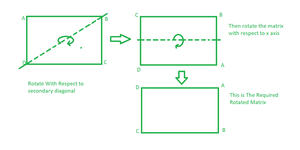
 Rotate square matrix 90 degrees in a clockwise direction

Below is the implementation of the above approach:

C++

#include <bits/stdc++.h>
using namespace std;

#define N 4

void print(int arr[N][N])
{
    for(int i = 0; i < N; ++i)
    {
        for(int j = 0; j < N; ++j)
            cout << arr[i][j] << " ";

        cout << '\n';
    }
}

void rotate(int arr[N][N])
{

    // First rotation
    // with respect to Secondary diagonal
    for(int i = 0; i < N; i++)
    {
        for(int j = 0; j < N - i; j++)
        {
            int temp = arr[i][j];
            arr[i][j] = arr[N - 1 - j][N - 1 - i];
            arr[N - 1 - j][N - 1 - i] = temp;
        }
    }

    // Second rotation
    // with respect to middle row
    for(int i = 0; i < N / 2; i++)
    {
        for(int j = 0; j < N; j++)
        {
            int temp = arr[i][j];
            arr[i][j] = arr[N - 1 - i][j];
            arr[N - 1 - i][j] = temp;
        }
    }
}

// Driver code
int main()
{
    int arr[N][N] = { { 1, 2, 3, 4 },
                      { 5, 6, 7, 8 },
                      { 9, 10, 11, 12 },
                      { 13, 14, 15, 16 } };
    rotate(arr);
    print(arr);
    return 0;
}

// This code is contributed  by Rahul Verma

Java

import java.io.*;

class GFG {

    static void rotate(int[][] arr)
    {

        int n = arr.length;

        // first rotation
        // with respect to Secondary diagonal
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n - i; j++) {
                int temp = arr[i][j];
                arr[i][j] = arr[n - 1 - j][n - 1 - i];
                arr[n - 1 - j][n - 1 - i] = temp;
            }
        }
        // Second rotation
        // with respect to middle row
        for (int i = 0; i < n / 2; i++) {
            for (int j = 0; j < n; j++) {
                int temp = arr[i][j];
                arr[i][j] = arr[n - 1 - i][j];
                arr[n - 1 - i][j] = temp;
            }
        }
    }

    // to print matrix
    static void printMatrix(int arr[][])
    {
        int n = arr.length;
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++)
                System.out.print(arr[i][j] + " ");
            System.out.println();
        }
    }
    // Driver code
    public static void main(String[] args)
    {
        int arr[][] = { { 1, 2, 3, 4 },
                        { 5, 6, 7, 8 },
                        { 9, 10, 11, 12 },
                        { 13, 14, 15, 16 } };
        rotate(arr);
        printMatrix(arr);
    }
}
// This code is contributed  by Rahul Verma

Python3

# Python3 implementation of above approach
N = 4

def display(arr):
    for i in range(N) :
        for j in range(N) :
            print(arr[i][j],end=" ")
        print()

# Function to rotate the matrix 90 degree clockwise
def rotate90Clockwise(arr) :
    global N

    # First rotation
    # with respect to Secondary diagonal
    for i in range(N) :
        for j in range(N-i) :
            arr[i][j],arr[N - 1 - j][N - 1 - i]=arr[N - 1 - j][N - 1 - i],arr[i][j]

    # Second rotation
    # with respect to middle row
    for i in range(N//2) :
        for j in range(N) :
            arr[i][j],arr[N - 1 - i][j]=arr[N - 1 - i][j],arr[i][j]

# Driver code
arr = [ [ 1, 2, 3, 4 ],
          [ 5, 6, 7, 8 ],
          [ 9, 10, 11, 12 ],
          [ 13, 14, 15, 16 ] ]
rotate90Clockwise(arr)
display(arr)

# This code is contributed by Aarti_Rathi

C#

using System;
using System.Collections.Generic;

class GFG{

static void rotate(int[,] arr)
{
    int n = arr.GetLength(0);

    // First rotation
    // with respect to Secondary diagonal
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n - i; j++)
        {
            int temp = arr[i, j];
            arr[i, j] = arr[n - 1 - j, n - 1 - i];
            arr[n - 1 - j, n - 1 - i] = temp;
        }
    }

    // Second rotation
    // with respect to middle row
    for(int i = 0; i < n / 2; i++)
    {
        for(int j = 0; j < n; j++)
        {
            int temp = arr[i, j];
            arr[i, j] = arr[n - 1 - i, j];
            arr[n - 1 - i, j] = temp;
        }
    }
}

// To print matrix
static void printMatrix(int [,]arr)
{
    int n = arr.GetLength(0);
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            Console.Write(arr[i, j] + " ");

        Console.WriteLine();
    }
}

// Driver code
public static void Main(String[] args)
{
    int [,]arr = { { 1, 2, 3, 4 },
                   { 5, 6, 7, 8 },
                   { 9, 10, 11, 12 },
                   { 13, 14, 15, 16 } };
    rotate(arr);
    printMatrix(arr);
}
}

// This code is contributed by aashish1995

Javascript

<script>
    function rotate(arr) {

        var n = arr.length;

        // first rotation
        // with respect to Secondary diagonal
        for (i = 0; i < n; i++) {
            for (j = 0; j < n - i; j++) {
                var temp = arr[i][j];
                arr[i][j] = arr[n - 1 - j][n - 1 - i];
                arr[n - 1 - j][n - 1 - i] = temp;
            }
        }

        // Second rotation
        // with respect to middle row
        for (i = 0; i < n / 2; i++) {
            for (j = 0; j < n; j++) {
                var temp = arr[i][j];
                arr[i][j] = arr[n - 1 - i][j];
                arr[n - 1 - i][j] = temp;
            }
        }
    }

    // to print matrix
    function printMatrix(arr) {
        var n = arr.length;
        for (i = 0; i < n; i++) {
            for (j = 0; j < n; j++)
                document.write(arr[i][j] + " ");
            document.write("<br/>");
        }
    }

    // Driver code
        var arr = [ [ 1, 2, 3, 4 ],
        [ 5, 6, 7, 8 ],
        [ 9, 10, 11, 12 ],
        [ 13, 14, 15, 16 ] ];
        rotate(arr);
        printMatrix(arr);

// This code is contributed by gauravrajput1
</script>

Output

13 9 5 1 
14 10 6 2 
15 11 7 3 
16 12 8 4 

Complexity Analysis:

Time Complexity – O(n*n)

Auxiliary Space – O(1)

Method 5: 

Approach: We first transpose the given matrix, and then reverse the content of individual rows to get the resultant 90 degree clockwise rotated matrix.

1  2  3                                                1  4  7                                                                 7  4  1

4  5  6        ——Transpose——>    2  5  8         —-Reverse individual rows—->    8  5  2     (Resultant matrix)

7  8  9                                                3  6  9                                                                 9  6  3

Below is the implementation of the above approach:

C++

#include <iostream>
using namespace std;
const int n = 4;
void print(int mat[n][n])
{
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++)
            cout << mat[i][j] << " ";
        cout << endl;
    }
}
void rotate90clockwise(int mat[n][n])
{
    // Transpose of matrix
    for (int i = 0; i < n; i++)
        for (int j = i + 1; j < n; j++)
            swap(mat[i][j], mat[j][i]);
    // Reverse individual rows
    for (int i = 0; i < n; i++) {
        int low = 0, high = n - 1;
        while (low < high) {
            swap(mat[i][low], mat[i][high]);
            low++;
            high--;
        }
    }
}
int main()
{
    int mat[n][n]
        = { { 1, 2, 3, 4 },
                      { 5, 6, 7, 8 },
                      { 9, 10, 11, 12 },
                      { 13, 14, 15, 16 } };
    rotate90clockwise(mat);
    print(mat);
}

Java

import java.util.*;

class GFG {
    static int n = 4;

    static void print(int mat[][]) {
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++)
                System.out.print(mat[i][j] + " ");
            System.out.println();
        }
    }

    static void rotate90clockwise(int mat[][])
    {

        // Transpose of matrix
        for (int i = 0; i < n; i++)
            for (int j = i + 1; j < n; j++) {
                int t = mat[i][j];
                mat[i][j] = mat[j][i];
                mat[j][i] = t;
            }

        // Reverse individual rows
        for (int i = 0; i < n; i++) {
            int low = 0, high = n - 1;
            while (low < high) {
                int t = mat[i][low];
                mat[i][low] = mat[i][high];
                mat[i][high] = t;
                low++;
                high--;
            }
        }
    }

  // Driver code
    public static void main(String[] args) {
        int mat[][] = { { 1, 2, 3, 4 },
                       { 5, 6, 7, 8 },
                       { 9, 10, 11, 12 },
                       { 13, 14, 15, 16 } };
        rotate90clockwise(mat);
        print(mat);
    }
}


// This code is contributed by umadevi9616

Python3

# Python3 implementation of above approach
N = 4

def display(arr):
    for i in range(N) :
        for j in range(N) :
            print(arr[i][j],end=" ")
        print()

# Function to rotate the matrix 90 degree clockwise
def rotate90Clockwise(arr) :
    global N

    # Transpose of matrix
    for i in range(N) :
        for j in range(i+1,N) :
            arr[i][j],arr[j][i]=arr[j][i],arr[i][j]

    # Reverse individual rows
    for i in range(N//2) :
        low = 0
        high = N-1
        while (low<high) :
            arr[i][low],arr[i][high]=arr[i][high],arr[i][low]
            low = low + 1
            high = high - 1

# Driver code
arr = [ [ 1, 2, 3, 4 ],
          [ 5, 6, 7, 8 ],
          [ 9, 10, 11, 12 ],
          [ 13, 14, 15, 16 ] ]
rotate90Clockwise(arr)
display(arr)

# This code is contributed by Aarti_Rathi

C#

using System;
using System.Collections.Generic;

class GFG{

static void rotate90clockwise(int[,] arr)
{
    int n = arr.GetLength(0);

    // Transpose of matrix
    for(int i = 0; i < n; i++)
    {
        for(int j = i+1; j < n; j++)
        {
            int temp = arr[i, j];
            arr[i, j] = arr[j, i];
            arr[j, i] = temp;
        }
    }

    /// Reverse individual rows
    for (int i = 0; i < n; i++) {
        int low = 0, high = n - 1;
        while (low < high) {
            int temp = arr[i, low];
            arr[i, low] = arr[i, high];
            arr[i, high] = temp;
            low++;
            high--;
        }
    }
}

// To print matrix
static void printMatrix(int [,]arr)
{
    int n = arr.GetLength(0);
    for(int i = 0; i < n; i++)
    {
        for(int j = 0; j < n; j++)
            Console.Write(arr[i, j] + " ");

        Console.WriteLine();
    }
}

// Driver code
public static void Main(String[] args)
{
    int [,]arr = { { 1, 2, 3, 4 },
                   { 5, 6, 7, 8 },
                   { 9, 10, 11, 12 },
                   { 13, 14, 15, 16 } };
    rotate90clockwise(arr);
    printMatrix(arr);
}
}

// This code is contributed by Aarti_Rathi

Javascript

<script>
    function rotate(arr) {

        var n = arr.length;

        // Transpose of matrix
        for (i = 0; i < n; i++) {
            for (j = i+1; j < n; j++) {
                var temp = arr[i][j];
                arr[i][j] = arr[j][i];
                arr[j][i] = temp;
            }
        }

        // Reverse individual rows
        for (i = 0; i < n; i++) {
            var low = 0, high = n-1;
            while (low < high) {
                var temp = arr[i][low];
                arr[i][low] = arr[i][high];
                arr[i][high] = temp;
                low++;
                high--;
            }
        }
    }

    // to print matrix
    function printMatrix(arr) {
        var n = arr.length;
        for (i = 0; i < n; i++) {
            for (j = 0; j < n; j++)
                document.write(arr[i][j] + " ");
            document.write("<br/>");
        }
    }

    // Driver code
    var arr = [ [ 1, 2, 3, 4 ],
    [ 5, 6, 7, 8 ],
    [ 9, 10, 11, 12 ],
    [ 13, 14, 15, 16 ] ];
    rotate(arr);
    printMatrix(arr);

// This code is contributed by Aarti_Rathi
</script>

Output

13 9 5 1 
14 10 6 2 
15 11 7 3 
16 12 8 4 

Complexity Analysis:

Time Complexity – O(n*n)

Auxiliary Space – O(1)