Rank of a Matrix: Definition, Properties, and Formula

Rank of a Matrix is defined as the dimension of the vector space formed by its columns. Rank of a Matrix is a very important concept in the field of Linear Algebra, as it helps us to know if we can find a solution to the system of equations or not. Rank of a matrix also helps us know the dimensionality of its vector space.

This article explores, the concept of the Rank of a Matrix in detail including its definition, how to calculate the rank of the matrix as well as a nullity and its relation with rank. We will also learn how to solve some problems based on the rank of a matrix. So, let’s start with the definition of the rank of the matrix first.

What is Rank of Matrix?

Rank of a Matrix is a fundamental concept in Linear Algebra, which measures the maximum number of linearly independent rows or columns in any matrix. In other words, it tells you how many of the rows or columns of a matrix are not useful and contribute to the overall information or dimensionality of the matrix. Let’s define the Rank of a Matrix.

Rank of a Matrix Definition

Rank of a matrix is defined as the number of linearly independent rows in a matrix.

It is denoted using ρ(A) where A is any matrix. Thus the number of rows of a matrix is a limit on the rank of the matrix, which means the rank of the matrix cannot exceed the total number of rows in a matrix.

For example, if a matrix is of the order 3×3 then the maximum rank of a matrix can be 3.

Note: If a matrix has all rows with zero elements, then the rank of a matrix is said to be zero.

Nullity of Matrix

In a given matrix, the number of vectors in the null space is called the nullity of the matrix or it can also be defined as the dimension of the null space of the given matrix.

Total columns in a matrix = Rank + Nullity

How To Calculate Rank of a Matrix?

There are 3 methods which can be used to get the rank of any given matrix. These methods are as follows:

• Minor Method
• Using Echelon Form
• Using Normal Form

Let’s discuss these methods in detail.

Minor Method

Pre-Requisite: Minors of Matrix

In order to find the rank of a matrix using minor method, following steps are followed:

• Calculate the determinant of the matrix (say A). If det(A) ≠ 0, then rank of matrix A = order of matrix A.
• If det(A) = 0, then the rank of the matrix is equal to order of the maximum possible non zero minor of the matrix.

Let us understand how to find the rank of matrix using minor method.

Example: Find the rank of matrix 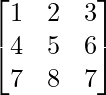using minor method.

Given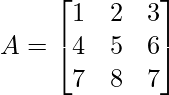

• Step 1: Calculate the determinant of A

det(A) = 1 (35 – 48) – 2 (28 – 42) + 3 (32 – 35)

det(A) = -13 + 28 + 9 = 24

• As det(A) ≠ 0, ρ(A) = order of A = 3

Using Echelon Form

The minor method becomes very tedious if the order of the matrix is very large. So in this case, we convert the matrix into Echelon Form. A matrix that is in upper triangular form or lower triangular form is considered to be in Echelon Form. A matrix can be converted to its Echelon Form by using elementary row operations. Following steps are followed to calculate the rank of a matrix using Echelon form:

• Convert the given matrix into its Echelon Form.
• The number of non-zero rows obtained in the Echelon form of the matrix is the rank of the matrix.

Let us understand how to find the rank of matrix using minor method.

Example: Find the rank of matrix 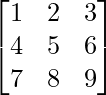using Echelon form method.

Given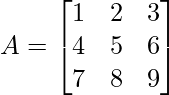

• Step 1: Convert A to echelon form

Apply R₂ = R₂ – 4R₁

Apply R₃ = R₃ – 7R₁

Apply R₃ = R₃ – 2R₂

As matrix A is now in lower triangular form, it is in Echelon Form.

• Step 2: Number of non-zero rows in A = 2. Thus ρ(A) = 2

Using Normal Form

A matrix is said to be in normal form if it can be reduced to the form 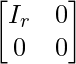. Here I_r represents the identity matrix of order r. If a matrix can be converted to its normal form, then rank of the matrix is said to be r.

Let us understand how to find the rank of matrix using minor method.

Example: Find the rank of matrix using normal form method.

Given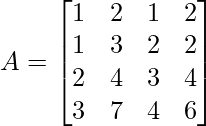

Apply R₂ = R₂ – R₁ , R₃ = R₃ – 2R₁ and R₄ = R₄ – 3R₁

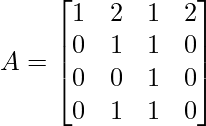
Apply R₁ = R₁ – 2R₂ and R₄ = R₄ – R₂

Apply R₁ = R₁ + R₃ and R₂ = R₂ – R₃

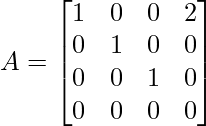
Apply C₄ → C₄ – 2C₁

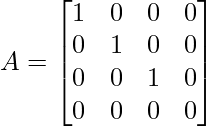
Thus A can be written as .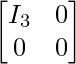

Thus, ρ(A) = 3

Properties of Rank of Matrix

Properties of rank of matrix is as follows:

• Rank of a matrix is equal to the order of the matrix if it is a non-singular matrix.
• Rank of a matrix is equal to the number of non-zero rows if it is in Echelon Form.
• Rank of matrix is equal to the order of identity matrix in it if it is in normal form.
• Rank of matrix < Order of matrix if it is singular matrix.
• Rank of matrix < minimum {m, n} if it is a rectangular matrix of order m x n.
• Rank of identity matrix is equal to the order of the identity matrix.
• Rank of a zero matrix or a null matrix is zero.

Read More,

• Types of Matrices
• Transpose of a Matrix
• Inverse of Matrix

Examples of Rank of a Matrix

Example 1: Find the rank of matrix 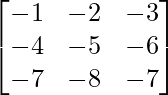using minor method.

Solution:

Given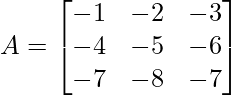

Step 1: Calculate the determinant of A

det(A) = -1 (35 – 48) + 2 (28 – 42) – 3 (32 – 35)

det(A) = 13 – 28 – 9 = -24

As det(A) ≠ 0, ρ(A) = order of A = 3

Example 2. Find the rank of matrix using minor method.

Solution:

Given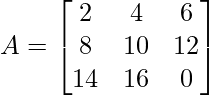

Step 1: Calculate the determinant of A

det(A) = 2(0-192) – 4(0-168) + 6(128-140)

det(A) = -384 + 672 – 72 = 216

As det(A) ≠ 0, ρ(A) = order of A = 3

Example 3. Find the rank of matrix 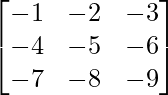using Echelon form method.

Solution:

Given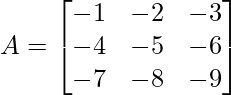

Step 1: Convert A to echelon form

Apply R₂ = R₂ – 4R₁

Apply R₃ = R₃ – 7R₁

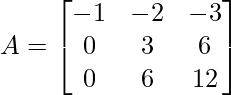
Apply R₃ = R₃ – 2R₂

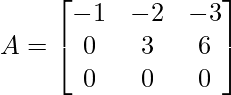
As matrix A is now in lower triangular form, it is in Echelon Form.

Step 2: Number of non-zero rows in A = 2. Thus ρ(A) = 2

Example 4. Find the rank of matrix 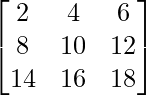using Echelon form method.

Solution:

Given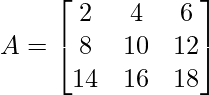

Step 1: Convert A to echelon form

Apply R₂ = R₂ – 4R₁

Apply R₃ = R₃ – 7R₁

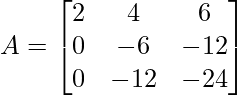
Apply R₃ = R₃ – 2R₂

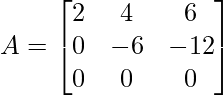
As matrix A is now in lower triangular form, it is in Echelon Form.

Step 2: Number of non-zero rows in A = 2. Thus ρ(A) = 2

Example 5. Find the rank of matrix using normal form method.

Solution:

Given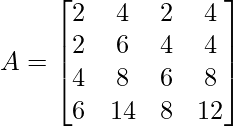

Apply R₂ = R₂ – R₁ , R₃ = R₃ – 2R₁ and R₄ = R₄ – 3R₁

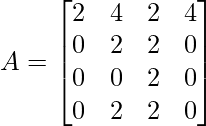
Apply R₁ = R₁ – 2R₂ and R4 = R₄ – R₂

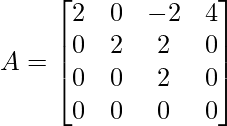
Apply R₁ = R₁ + R₃ and R₂ = R₂ – R₃

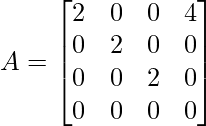
Apply C₄ → C₄ – 2C₁

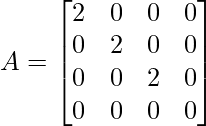
Apply R₁ = R₁/2, R₂ = R₂/2, R₃ = R₃/2

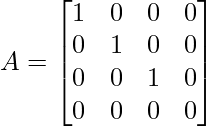
Thus A can be written as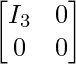

Thus, ρ(A) = 3

Rank of a Matrix – FAQs

1. Define Rank of a Matrix.

Rank of a matrix is defined as the number of linearly independent rows in a matrix. It is denoted using ρ(A) where A is any matrix.

2. How to Find the Rank of a Matrix?

Rank of matrix can be calculated using various methods such as:

• Minor Method
• Using Echelon Form
• Using Normal Form

3. What is the Rank of Matrix if Determinant of Matrix is not Equal to Zero?

If determinant of a matrix is zero, then the rank of the matrix is equal to the order of the matrix.

4. When is a Matrix said to be in Echelon form?

A matrix which is in upper triangular form or in lower triangular form is said to be in echelon form.

5. What is Normal Form of the Matrix?

A matrix is said to be in normal form if it can be written as 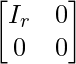where I_r is the identity matrix of the order ‘r’.

6. What is the Rank of Null Matrix?

Rank of a null matrix is zero.

7. What is the Rank of an Identity Matrix?

Rank of an identity matrix is equal to the order of the matrix.

8. What is the Relationship Between Nullity and Rank of a Matrix?

Relationship between nullity and rank of a matrix is:

Total columns in a matrix = Rank + Nullity