Python | sympy.fibonacci() method
Last Updated :
15 Nov, 2022
With the help of sympy.fibonacci() method, we can find the Fibonacci number and Fibonacci polynomial in SymPy.
fibonacci(n) – The Fibonacci numbers are the integer sequence defined by the initial terms 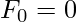 ,
, 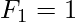 and the two-term recurrence relation
and the two-term recurrence relation 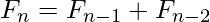 .
.
Syntax: fibonacci(n) Parameter: n – It denotes the number upto which Fibonacci number is to be calculated. Returns: Returns the nth Fibonacci number.
Example #1:
Python3
from sympy import *
n = 7
print("Value of n = {}".format(n))
nth_fibonacci = fibonacci(n)
print("Value of nth fibonacci number : {}".format(nth_fibonacci))
|
Output:
Value of n = 7
Value of nth fibonacci number : 13
fibonacci(n, k) –
The Fibonacci polynomials are defined by 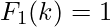 ,
, 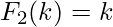 , and
, and 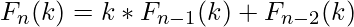 for
for 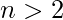 . For all positive integers
. For all positive integers 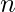 ,
, 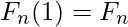 .
.
Syntax: fibonacci(n, k) Parameter: n – It denotes the nth Fibonacci polynomial. k – It denotes the variable in the Fibonacci polynomial. Returns: Returns the nth Fibonacci polynomial in k, Fn(k)
Example #2:
Python3
from sympy import *
n = 5
k = symbols('x')
print("Value of n = {} and k = {}".format(n, k))
nth_fibonacci_poly = fibonacci(n, k)
print("The nth fibonacci polynomial : {}".format(nth_fibonacci_poly))
|
Output:
Value of n = 5 and k = x
The nth fibonacci polynomial : x**4 + 3*x**2 + 1
Example #3:
Python3
from sympy import *
n = 6
k = 3
print("Value of n = {} and k = {}".format(n, k))
nth_fibonacci_poly = fibonacci(n, k)
print("The nth fibonacci polynomial value : {}".format(nth_fibonacci_poly))
|
Output:
Value of n = 6 and k = 3
The nth fibonacci polynomial value : 360
Share your thoughts in the comments
Please Login to comment...