stdev() method in Python statistics module
Last Updated :
11 Nov, 2022
Statistics module in Python provides a function known as stdev() , which can be used to calculate the standard deviation. stdev() function only calculates standard deviation from a sample of data, rather than an entire population.
To calculate standard deviation of an entire population, another function known as pstdev() is used.
Standard Deviation is a measure of spread in Statistics. It is used to quantify the measure of spread, variation of a set of data values. It is very much similar to variance, gives the measure of deviation whereas variance provides the squared value.
A low measure of Standard Deviation indicates that the data are less spread out, whereas a high value of Standard Deviation shows that the data in a set are spread apart from their mean average values. A useful property of the standard deviation is that, unlike the variance, it is expressed in the same units as the data.
Standard Deviation is calculated by :
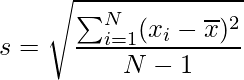 where x1, x2, x3.....xn are observed values in sample data,
where x1, x2, x3.....xn are observed values in sample data,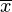 is the mean value of observations andN is the number of sample observations.
is the mean value of observations andN is the number of sample observations.
Syntax : stdev( [data-set], xbar )
Parameters :
[data] : An iterable with real valued numbers.
xbar (Optional): Takes actual mean of data-set as value.
Returntype : Returns the actual standard deviation of the values passed as parameter.
Exceptions :
StatisticsError is raised for data-set less than 2 values passed as parameter.
Impossible/precision-less values when the value provided as xbar doesn’t match actual mean of the data-set.
Code #1 :
Python3
import statistics
sample = [1, 2, 3, 4, 5]
print("Standard Deviation of sample is % s "
% (statistics.stdev(sample)))
|
Output :
Standard Deviation of the sample is 1.5811388300841898
Code #2 : Demonstrate stdev() on a varying set of data types
Python3
from statistics import stdev
from fractions import Fraction as fr
sample1 = (1, 2, 5, 4, 8, 9, 12)
sample2 = (-2, -4, -3, -1, -5, -6)
sample3 = (-9, -1, -0, 2, 1, 3, 4, 19)
sample4 = (1.23, 1.45, 2.1, 2.2, 1.9)
print("The Standard Deviation of Sample1 is % s"
%(stdev(sample1)))
print("The Standard Deviation of Sample2 is % s"
%(stdev(sample2)))
print("The Standard Deviation of Sample3 is % s"
%(stdev(sample3)))
print("The Standard Deviation of Sample4 is % s"
%(stdev(sample4)))
|
Output :
The Standard Deviation of Sample1 is 3.9761191895520196
The Standard Deviation of Sample2 is 1.8708286933869707
The Standard Deviation of Sample3 is 7.8182478855559445
The Standard Deviation of Sample4 is 0.41967844833872525
Code #3 :Demonstrate the difference between results of variance() and stdev()
Python3
import statistics
sample = [1, 2, 3, 4, 5]
print("Standard Deviation of the sample is % s "
%(statistics.stdev(sample)))
print("Variance of the sample is % s"
%(statistics.variance(sample)))
|
Output :
Standard Deviation of the sample is 1.5811388300841898
Variance of the sample is 2.5
Code #4 : Demonstrate the use of xbar parameter
Python3
import statistics
sample = (1, 1.3, 1.2, 1.9, 2.5, 2.2)
m = statistics.mean(sample)
print("Standard Deviation of Sample set is % s"
%(statistics.stdev(sample, xbar = m)))
|
Output :
Standard Deviation of Sample set is 0.6047037842337906
Code #5 : Demonstrates StatisticsError
Python3
import statistics
sample = [1]
print(statistics.stdev(sample))
|
Output :
Traceback (most recent call last):
File "/home/f921f9269b061f1cc4e5fc74abf6ce10.py", line 12, in
print(statistics.stdev(sample))
File "/usr/lib/python3.5/statistics.py", line 617, in stdev
var = variance(data, xbar)
File "/usr/lib/python3.5/statistics.py", line 555, in variance
raise StatisticsError('variance requires at least two data points')
statistics.StatisticsError: variance requires at least two data points
Applications :
- Standard Deviation is highly essential in the field of statistical maths and statistical study. It is commonly used to measure confidence in statistical calculations. For example, the margin of error in calculating marks of an exam is determined by calculating the expected standard deviation in the results if the same exam were to be conducted multiple times.
- It is very useful in the field of financial studies as well as it helps to determine the margin of profit and loss. The standard deviation is also important, where the standard deviation on the rate of return on an investment is a measure of the volatility of the investment.
Share your thoughts in the comments
Please Login to comment...