Push Relabel Algorithm | Set 2 (Implementation)

We strongly recommend to refer below article before moving on to this article. 
Push Relabel Algorithm | Set 1 (Introduction and Illustration)

Problem Statement:

Given a graph that represents a flow network where every edge has a capacity. Also given two vertices source ‘s’ and sink ‘t’ in the graph, find the maximum possible flow from s to t with following constraints:

1. Flow on an edge doesn’t exceed the given capacity of the edge.
2. Incoming flow is equal to outgoing flow for every vertex except s and t.

For example, consider the following graph from CLRS book.  

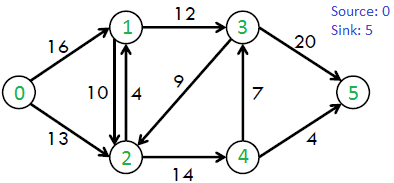
The maximum possible flow in the above graph is 23. 

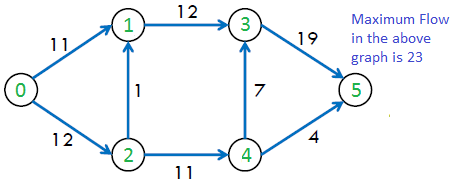
Push-Relabel Algorithm 
1) Initialize PreFlow : Initialize Flows and Heights 

2) While it is possible to perform a Push() or Relabel() on a vertex
   // Or while there is a vertex that has excess flow
           Do Push() or Relabel()

// At this point all vertices have Excess Flow as 0 (Except source
// and sink)
3) Return flow.

Below are main operations performed in Push Relabel algorithm.  

There are three main operations in Push-Relabel Algorithm

1. Initialize PreFlow() It initializes heights and flows of all vertices. 

Preflow() 
1) Initialize height and flow of every vertex as 0.
2) Initialize height of source vertex equal to total 
   number of vertices in graph.
3) Initialize flow of every edge as 0.
4) For all vertices adjacent to source s, flow and  
   excess flow is equal to capacity initially.

2. Push() is used to make the flow from a node that has excess flow. If a vertex has excess flow and there is an adjacent with a smaller height (in the residual graph), we push the flow from the vertex to the adjacent with a lower height. The amount of pushed flow through the pipe (edge) is equal to the minimum of excess flow and capacity of the edge.

3. Relabel() operation is used when a vertex has excess flow and none of its adjacents is at the lower height. We basically increase the height of the vertex so that we can perform push(). To increase height, we pick the minimum height adjacent (in residual graph, i.e., an adjacent to whom we can add flow) and add 1 to it.

Implementation:

The following implementation uses the below structure for representing a flow network. 

struct Vertex 
{
   int h;      // Height of node
   int e_flow; // Excess Flow 
}

struct Edge 
{
   int u, v; // Edge is from u to v       
   int flow; // Current flow
   int capacity; 
}

class Graph 
{
   Edge edge[];   // Array of edges
   Vertex ver[];  // Array of vertices 
}

The below code uses the given graph itself as a flow network and residual graph. We have not created a separate graph for the residual graph and have used the same graph for simplicity.

Implementation:

C++

// C++ program to implement push-relabel algorithm for
// getting maximum flow of graph
#include <bits/stdc++.h>
using namespace std;

struct Edge
{
    // To store current flow and capacity of edge
    int flow, capacity;

    // An edge u--->v has start vertex as u and end
    // vertex as v.
    int u, v;

    Edge(int flow, int capacity, int u, int v)
    {
        this->flow = flow;
        this->capacity = capacity;
        this->u = u;
        this->v = v;
    }
};

// Represent a Vertex
struct Vertex
{
    int h, e_flow;

    Vertex(int h, int e_flow)
    {
        this->h = h;
        this->e_flow = e_flow;
    }
};

// To represent a flow network
class Graph
{
    int V;    // No. of vertices
    vector<Vertex> ver;
    vector<Edge> edge;

    // Function to push excess flow from u
    bool push(int u);

    // Function to relabel a vertex u
    void relabel(int u);

    // This function is called to initialize
    // preflow
    void preflow(int s);

    // Function to reverse edge
    void updateReverseEdgeFlow(int i, int flow);

public:
    Graph(int V);  // Constructor

    // function to add an edge to graph
    void addEdge(int u, int v, int w);

    // returns maximum flow from s to t
    int getMaxFlow(int s, int t);
};

Graph::Graph(int V)
{
    this->V = V;

    // all vertices are initialized with 0 height
    // and 0 excess flow
    for (int i = 0; i < V; i++)
        ver.push_back(Vertex(0, 0));
}

void Graph::addEdge(int u, int v, int capacity)
{
    // flow is initialized with 0 for all edge
    edge.push_back(Edge(0, capacity, u, v));
}

void Graph::preflow(int s)
{
    // Making h of source Vertex equal to no. of vertices
    // Height of other vertices is 0.
    ver[s].h = ver.size();

    //
    for (int i = 0; i < edge.size(); i++)
    {
        // If current edge goes from source
        if (edge[i].u == s)
        {
            // Flow is equal to capacity
            edge[i].flow = edge[i].capacity;

            // Initialize excess flow for adjacent v
            ver[edge[i].v].e_flow += edge[i].flow;

            // Add an edge from v to s in residual graph with
            // capacity equal to 0
            edge.push_back(Edge(-edge[i].flow, 0, edge[i].v, s));
        }
    }
}

// returns index of overflowing Vertex
int overFlowVertex(vector<Vertex>& ver)
{
    for (int i = 1; i < ver.size() - 1; i++)
       if (ver[i].e_flow > 0)
            return i;

    // -1 if no overflowing Vertex
    return -1;
}

// Update reverse flow for flow added on ith Edge
void Graph::updateReverseEdgeFlow(int i, int flow)
{
    int u = edge[i].v, v = edge[i].u;

    for (int j = 0; j < edge.size(); j++)
    {
        if (edge[j].v == v && edge[j].u == u)
        {
            edge[j].flow -= flow;
            return;
        }
    }

    // adding reverse Edge in residual graph
    Edge e = Edge(0, flow, u, v);
    edge.push_back(e);
}

// To push flow from overflowing vertex u
bool Graph::push(int u)
{
    // Traverse through all edges to find an adjacent (of u)
    // to which flow can be pushed
    for (int i = 0; i < edge.size(); i++)
    {
        // Checks u of current edge is same as given
        // overflowing vertex
        if (edge[i].u == u)
        {
            // if flow is equal to capacity then no push
            // is possible
            if (edge[i].flow == edge[i].capacity)
                continue;

            // Push is only possible if height of adjacent
            // is smaller than height of overflowing vertex
            if (ver[u].h > ver[edge[i].v].h)
            {
                // Flow to be pushed is equal to minimum of
                // remaining flow on edge and excess flow.
                int flow = min(edge[i].capacity - edge[i].flow,
                               ver[u].e_flow);

                // Reduce excess flow for overflowing vertex
                ver[u].e_flow -= flow;

                // Increase excess flow for adjacent
                ver[edge[i].v].e_flow += flow;

                // Add residual flow (With capacity 0 and negative
                // flow)
                edge[i].flow += flow;

                updateReverseEdgeFlow(i, flow);

                return true;
            }
        }
    }
    return false;
}

// function to relabel vertex u
void Graph::relabel(int u)
{
    // Initialize minimum height of an adjacent
    int mh = INT_MAX;

    // Find the adjacent with minimum height
    for (int i = 0; i < edge.size(); i++)
    {
        if (edge[i].u == u)
        {
            // if flow is equal to capacity then no
            // relabeling
            if (edge[i].flow == edge[i].capacity)
                continue;

            // Update minimum height
            if (ver[edge[i].v].h < mh)
            {
                mh = ver[edge[i].v].h;

                // updating height of u
                ver[u].h = mh + 1;
            }
        }
    }
}

// main function for printing maximum flow of graph
int Graph::getMaxFlow(int s, int t)
{
    preflow(s);

    // loop until none of the Vertex is in overflow
    while (overFlowVertex(ver) != -1)
    {
        int u = overFlowVertex(ver);
        if (!push(u))
            relabel(u);
    }

    // ver.back() returns last Vertex, whose
    // e_flow will be final maximum flow
    return ver.back().e_flow;
}

// Driver program to test above functions
int main()
{
    int V = 6;
    Graph g(V);

    // Creating above shown flow network
    g.addEdge(0, 1, 16);
    g.addEdge(0, 2, 13);
    g.addEdge(1, 2, 10);
    g.addEdge(2, 1, 4);
    g.addEdge(1, 3, 12);
    g.addEdge(2, 4, 14);
    g.addEdge(3, 2, 9);
    g.addEdge(3, 5, 20);
    g.addEdge(4, 3, 7);
    g.addEdge(4, 5, 4);

    // Initialize source and sink
    int s = 0, t = 5;

    cout << "Maximum flow is " << g.getMaxFlow(s, t);
    return 0;
}

Python3

# python program to implement push-relabel algorithm for
# getting maximum flow of graph
class Edge:

    def __init__(self, flow, capacity, u, v):
        self.flow = flow
        self.capacity = capacity
        self.u = u
        self.v = v

# Represent a Vertex
class Vertex:

    def __init__(self, h, e_flow):
        self.h = h
        self.e_flow = e_flow


# To represent a flow network
class Graph:

    # int V;    # No. of vertices
    # vector<Vertex> ver;
    # vector<Edge> edge;
    def __init__(self, V):

        self.V = V;
        self.edge = []
        self.ver = []
        # all vertices are initialized with 0 height
        # and 0 excess flow
        for i in range(V):
            self.ver.append(Vertex(0, 0))

    def addEdge(self, u, v, capacity):
        # flow is initialized with 0 for all edge
        self.edge.append(Edge(0, capacity, u, v))


    def preflow(self, s):

        # Making h of source Vertex equal to no. of vertices
        # Height of other vertices is 0.
        self.ver[s].h = len(self.ver);

        for i in range(len(self.edge)):

            # If current edge goes from source
            if (self.edge[i].u == s):
                # Flow is equal to capacity
                self.edge[i].flow = self.edge[i].capacity

                # Initialize excess flow for adjacent v
                self.ver[self.edge[i].v].e_flow += self.edge[i].flow

                # Add an edge from v to s in residual graph with
                # capacity equal to 0
                self.edge.append(Edge(-self.edge[i].flow, 0, self.edge[i].v, s))


    # returns index of overflowing Vertex
    def overFlowVertex(self):

        for i in range(1, len(self.ver)-1):

            if(self.ver[i].e_flow > 0):
                return i

        # -1 if no overflowing Vertex
        return -1


    # Update reverse flow for flow added on ith Edge
    def updateReverseEdgeFlow(self, i, flow):

        u = self.edge[i].v
        v = self.edge[i].u

        for j in range(0, len(self.edge)):
            if (self.edge[j].v == v and self.edge[j].u == u):
                self.edge[j].flow -= flow
                return

        # adding reverse Edge in residual graph
        e = Edge(0, flow, u, v)
        self.edge.append(e)


    # To push flow from overflowing vertex u
    def push(self, u):

        # Traverse through all edges to find an adjacent (of u)
        # to which flow can be pushed
        for i in range(0, len(self.edge)):

            # Checks u of current edge is same as given
            # overflowing vertex
            if (self.edge[i].u == u):
                # if flow is equal to capacity then no push
                # is possible
                if (self.edge[i].flow == self.edge[i].capacity):
                    continue;

                # Push is only possible if height of adjacent
                # is smaller than height of overflowing vertex
                if (self.ver[u].h > self.ver[self.edge[i].v].h):

                    # Flow to be pushed is equal to minimum of
                    # remaining flow on edge and excess flow.
                    flow = min(self.edge[i].capacity - self.edge[i].flow, self.ver[u].e_flow)

                    # Reduce excess flow for overflowing vertex
                    self.ver[u].e_flow -= flow;

                    # Increase excess flow for adjacent
                    self.ver[self.edge[i].v].e_flow += flow;

                    # Add residual flow (With capacity 0 and negative
                    # flow)
                    self.edge[i].flow += flow;

                    self.updateReverseEdgeFlow(i, flow);

                    return True;

        return False;


    # function to relabel vertex u
    def relabel(self, u):
        # Initialize minimum height of an adjacent
        mh = 2100000

        # Find the adjacent with minimum height
        for i in range(len(self.edge)):
            if (self.edge[i].u == u):

                # if flow is equal to capacity then no
                # relabeling
                if (self.edge[i].flow == self.edge[i].capacity):
                    continue;

                # Update minimum height
                if (self.ver[self.edge[i].v].h < mh):
                    mh = self.ver[self.edge[i].v].h;

                    # updating height of u
                    self.ver[u].h = mh + 1;


    # main function for printing maximum flow of graph
    def getMaxFlow(self, s, t):

        self.preflow(s);

        # loop until none of the Vertex is in overflow
        while (self.overFlowVertex() != -1):

            u = self.overFlowVertex();
            if (self.push(u) == False):
                self.relabel(u);

        # ver.back() returns last Vertex, whose
        # e_flow will be final maximum flow
        return self.ver[len(self.ver)-1].e_flow


# Driver program to test above functions
V = 6;
g = Graph(V);

# Creating above shown flow network
g.addEdge(0, 1, 16);
g.addEdge(0, 2, 13);
g.addEdge(1, 2, 10);
g.addEdge(2, 1, 4);
g.addEdge(1, 3, 12);
g.addEdge(2, 4, 14);
g.addEdge(3, 2, 9);
g.addEdge(3, 5, 20);
g.addEdge(4, 3, 7);
g.addEdge(4, 5, 4);

# Initialize source and sink
s = 0
t = 5;

print("Maximum flow is ",  g.getMaxFlow(s, t));

# The code is contributed by Arushi goel.

C#

// C# program to implement push-relabel algorithm for
// getting maximum flow of graph
using System;
using System.Collections.Generic;
using System.Collections;
using System.Linq;

class Edge
{
    public int flow;
    public int capacity;
    public int u;
    public int v;

    public Edge(int flow,int capacity,int u,int v)
    {
        this.flow = flow;
        this.capacity = capacity;
        this.u = u;
        this.v = v;
    }
}

// Represent a Vertex
class Vertex
{
    public int h;
    public int e_flow;
    public Vertex(int h,int e_flow)
    {
        this.h = h;
        this.e_flow = e_flow;
    }
}

// To represent a flow network
class Graph
{

    public int V;    // No. of vertices
    public List<Vertex> ver;
    public List<Edge> edge;
    public Graph(int V)
    {
        this.V = V;
        ver = new List<Vertex>();
        edge = new List<Edge>();
        // all vertices are initialized with 0 height
        // and 0 excess flow
        for (int i = 0; i < V; i++)
            ver.Add(new Vertex(0, 0));
    }

    public void addEdge(int u,int v,int capacity)
    {
        // flow is initialized with 0 for all edge
        edge.Add(new Edge(0, capacity, u, v));
    }


    public void preflow(int s)
    {
        // Making h of source Vertex equal to no. of vertices
        // Height of other vertices is 0.
        ver[s].h = ver.Count;

        //
        for (int i = 0; i < edge.Count; i++)
        {
            // If current edge goes from source
            if (edge[i].u == s)
            {
                // Flow is equal to capacity
                edge[i].flow = edge[i].capacity;

                // Initialize excess flow for adjacent v
                ver[edge[i].v].e_flow += edge[i].flow;

                // Add an edge from v to s in residual graph with
                // capacity equal to 0
                edge.Add(new Edge(-edge[i].flow, 0, edge[i].v, s));
            }
        }
    }

    // returns index of overflowing Vertex
    public int overFlowVertex()
    {
        for (int i = 1; i < ver.Count - 1; i++)
           if (ver[i].e_flow > 0)
                return i;

        // -1 if no overflowing Vertex
        return -1;
    }


    // Update reverse flow for flow added on ith Edge
    public void updateReverseEdgeFlow(int i,int  flow)
    {
        int u = edge[i].v;
        int v = edge[i].u;

        for (int j = 0; j < edge.Count; j++)
        {
            if (edge[j].v == v && edge[j].u == u)
            {
                edge[j].flow -= flow;
                return;
            }
        }

        // adding reverse Edge in residual graph
        Edge e = new Edge(0, flow, u, v);
        edge.Add(e);
    }

    // To push flow from overflowing vertex u
    public bool push(int u)
    {
        // Traverse through all edges to find an adjacent (of u)
        // to which flow can be pushed
        for (int i = 0; i < edge.Count; i++)
        {
            // Checks u of current edge is same as given
            // overflowing vertex
            if (edge[i].u == u)
            {
                // if flow is equal to capacity then no push
                // is possible
                if (edge[i].flow == edge[i].capacity)
                    continue;

                // Push is only possible if height of adjacent
                // is smaller than height of overflowing vertex
                if (ver[u].h > ver[edge[i].v].h)
                {
                    // Flow to be pushed is equal to minimum of
                    // remaining flow on edge and excess flow.
                    int flow = Math.Min(edge[i].capacity - edge[i].flow,
                                   ver[u].e_flow);

                    // Reduce excess flow for overflowing vertex
                    ver[u].e_flow -= flow;

                    // Increase excess flow for adjacent
                    ver[edge[i].v].e_flow += flow;

                    // Add residual flow (With capacity 0 and negative
                    // flow)
                    edge[i].flow += flow;

                    updateReverseEdgeFlow(i, flow);

                    return true;
                }
            }
        }
        return false;
    }


    // function to relabel vertex u
    public void relabel(int u)
    {
        // Initialize minimum height of an adjacent
        int mh = 2100000;

        // Find the adjacent with minimum height
        for (int i = 0; i < edge.Count; i++)
        {
            if (edge[i].u == u)
            {
                // if flow is equal to capacity then no
                // relabeling
                if (edge[i].flow == edge[i].capacity)
                    continue;

                // Update minimum height
                if (ver[edge[i].v].h < mh)
                {
                    mh = ver[edge[i].v].h;

                    // updating height of u
                    ver[u].h = mh + 1;
                }
            }
        }
    }

    // main function for printing maximum flow of graph
    public int getMaxFlow(int s,int  t)
    {
        preflow(s);

        // loop until none of the Vertex is in overflow
        while (overFlowVertex() != -1)
        {
            int u = overFlowVertex();
            if (!push(u))
                relabel(u);
        }

        // ver.back() returns last Vertex, whose
        // e_flow will be final maximum flow
        return ver[ver.Count-1].e_flow;
    }
}




class HelloWorld {


    static void Main() {

        // Driver program to test above functions
        int V = 6;
        Graph g = new Graph(V);

        // Creating above shown flow network
        g.addEdge(0, 1, 16);
        g.addEdge(0, 2, 13);
        g.addEdge(1, 2, 10);
        g.addEdge(2, 1, 4);
        g.addEdge(1, 3, 12);
        g.addEdge(2, 4, 14);
        g.addEdge(3, 2, 9);
        g.addEdge(3, 5, 20);
        g.addEdge(4, 3, 7);
        g.addEdge(4, 5, 4);

        // Initialize source and sink
        int s = 0, t = 5;

        Console.WriteLine("Maximum flow is " + g.getMaxFlow(s, t));
    }
}

// The code is contributed by Arushi jindal.

Javascript

// javascript program to implement push-relabel algorithm for
// getting maximum flow of graph
class Edge
{
    constructor(flow, capacity, u, v)
    {
        this.flow = flow;
        this.capacity = capacity;
        this.u = u;
        this.v = v;
    }
}

// Represent a Vertex
class Vertex
{

    constructor(h, e_flow)
    {
        this.h = h;
        this.e_flow = e_flow;
    }
}

// To represent a flow network
class Graph
{

    // int V;    // No. of vertices
    // vector<Vertex> ver;
    // vector<Edge> edge;
    constructor(V)
    {
        this.V = V;
        this.edge = new Array();
        this.ver = new Array();
        // all vertices are initialized with 0 height
        // and 0 excess flow
        for (let i = 0; i < V; i++)
            this.ver.push(new Vertex(0, 0));
    }

    addEdge(u, v, capacity)
    {
        // flow is initialized with 0 for all edge
        this.edge.push(new Edge(0, capacity, u, v));
    }


    preflow(s)
    {
        // Making h of source Vertex equal to no. of vertices
        // Height of other vertices is 0.
        this.ver[s].h = this.ver.length;

        //
        for (let i = 0; i < this.edge.length; i++)
        {
            // If current edge goes from source
            if (this.edge[i].u == s)
            {
                // Flow is equal to capacity
                this.edge[i].flow = this.edge[i].capacity;

                // Initialize excess flow for adjacent v
                this.ver[this.edge[i].v].e_flow += this.edge[i].flow;

                // Add an edge from v to s in residual graph with
                // capacity equal to 0
                this.edge.push(new Edge(-this.edge[i].flow, 0, this.edge[i].v, s));
            }
        }
    }

    // returns index of overflowing Vertex
    overFlowVertex()
    {
        for (let i = 1; i < this.ver.length - 1; i++)
           if (this.ver[i].e_flow > 0)
                return i;

        // -1 if no overflowing Vertex
        return -1;
    }


    // Update reverse flow for flow added on ith Edge
    updateReverseEdgeFlow(i, flow)
    {
        let u = this.edge[i].v;
        let v = this.edge[i].u;

        for (let j = 0; j < this.edge.length; j++)
        {
            if (this.edge[j].v == v && this.edge[j].u == u)
            {
                this.edge[j].flow -= flow;
                return;
            }
        }

        // adding reverse Edge in residual graph
        let e = new Edge(0, flow, u, v);
        this.edge.push(e);
    }

    // To push flow from overflowing vertex u
    push(u)
    {
        // Traverse through all edges to find an adjacent (of u)
        // to which flow can be pushed
        for (let i = 0; i < this.edge.length; i++)
        {
            // Checks u of current edge is same as given
            // overflowing vertex
            if (this.edge[i].u == u)
            {
                // if flow is equal to capacity then no push
                // is possible
                if (this.edge[i].flow == this.edge[i].capacity)
                    continue;

                // Push is only possible if height of adjacent
                // is smaller than height of overflowing vertex
                if (this.ver[u].h > this.ver[this.edge[i].v].h)
                {
                    // Flow to be pushed is equal to minimum of
                    // remaining flow on edge and excess flow.
                    let flow = Math.min(this.edge[i].capacity - this.edge[i].flow,
                                   this.ver[u].e_flow);

                    // Reduce excess flow for overflowing vertex
                    this.ver[u].e_flow -= flow;

                    // Increase excess flow for adjacent
                    this.ver[this.edge[i].v].e_flow += flow;

                    // Add residual flow (With capacity 0 and negative
                    // flow)
                    this.edge[i].flow += flow;

                    this.updateReverseEdgeFlow(i, flow);

                    return true;
                }
            }
        }
        return false;
    }


    // function to relabel vertex u
    relabel(u)
    {
        // Initialize minimum height of an adjacent
        let mh = 2100000;

        // Find the adjacent with minimum height
        for (let i = 0; i < this.edge.length; i++)
        {
            if (this.edge[i].u == u)
            {
                // if flow is equal to capacity then no
                // relabeling
                if (this.edge[i].flow == this.edge[i].capacity)
                    continue;

                // Update minimum height
                if (this.ver[this.edge[i].v].h < mh)
                {
                    mh = this.ver[this.edge[i].v].h;

                    // updating height of u
                    this.ver[u].h = mh + 1;
                }
            }
        }
    }

    // main function for printing maximum flow of graph
    getMaxFlow(s, t)
    {
        this.preflow(s);

        // loop until none of the Vertex is in overflow
        while (this.overFlowVertex() != -1)
        {
            let u = this.overFlowVertex();
            if (!this.push(u))
                this.relabel(u);
        }

        // ver.back() returns last Vertex, whose
        // e_flow will be final maximum flow
        return this.ver[this.ver.length-1].e_flow;
    }
}

















// Driver program to test above functions
let V = 6;
let g = new Graph(V);

// Creating above shown flow network
g.addEdge(0, 1, 16);
g.addEdge(0, 2, 13);
g.addEdge(1, 2, 10);
g.addEdge(2, 1, 4);
g.addEdge(1, 3, 12);
g.addEdge(2, 4, 14);
g.addEdge(3, 2, 9);
g.addEdge(3, 5, 20);
g.addEdge(4, 3, 7);
g.addEdge(4, 5, 4);

// Initialize source and sink
let s = 0, t = 5;

console.log("Maximum flow is " + g.getMaxFlow(s, t));

// The code is contributed by Nidhi goel.

Output

Maximum flow is 23

The code in this article is contributed by Siddharth Lalwani and Utkarsh Trivedi.