Program to compute Log n

Write a one-line C function that calculates and returns 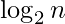. For example, if n = 64, then your function should return 6, and if n = 128, then your function should return 7. 

Using Recursion

C++

// C++ program to find log(n) using Recursion
#include <iostream>
using namespace std;

unsigned int Log2n(unsigned int n)
{
    return (n > 1) ? 1 + Log2n(n / 2) : 0;
}

// Driver code
int main()
{
    unsigned int n = 32;
    cout << Log2n(n);
    getchar();
    return 0;
}

// This code is contributed by kirti

C

// program to find log(n) using Recursion
#include <stdio.h>

unsigned int Log2n(unsigned int n)
{
    return (n > 1) ? 1 + Log2n(n / 2) : 0;
}

int main()
{
    unsigned int n = 32;
    printf("%u", Log2n(n));
    getchar();
    return 0;
}

Java

// Java program to find log(n)
// using Recursion
class Gfg1
{

    static int Log2n(int n)
    {
        return (n > 1) ? 1 + Log2n(n / 2) : 0;
    }

    // Driver Code
    public static void main(String args[])
    {
        int n = 32;
        System.out.println(Log2n(n));
    }
}

// This code is contributed by Niraj_Pandey

Python3

# Python 3 program to
# find log(n) using Recursion

def Log2n(n):

    return 1 + Log2n(n / 2) if (n > 1) else 0

# Driver code
n = 32
print(Log2n(n))

# This code is contributed by
# Smitha Dinesh Semwal

C#

// C# program to find log(n)
// using Recursion
using System;

class GFG {

    static int Log2n(int n)
    {
        return (n > 1) ? 1 +
            Log2n(n / 2) : 0;
    }

    // Driver Code
    public static void Main()
    {
        int n = 32;

        Console.Write(Log2n(n));
    }
}

// This code is contributed by
// nitin mittal.

Javascript

<script>
// program to find log(n) using Recursion


 function  Log2n( n)
{
    return (n > 1) ? 1 + Log2n(n / 2) : 0;
}

     n = 32;
    document.write( Log2n(n));
   //This code is contributed by simranarora5sos
</script>

Output :

5

Time complexity: O(log n) 
Auxiliary space: O(log n) if the stack size is considered during recursion otherwise O(1) 

Using inbuilt log function

We can use the inbuilt function of the standard library which is available in the library.  

C++

// C++ program to find log(n) using Inbuilt
#include <bits/stdc++.h>
using namespace std;

int main()
{
    unsigned int n = 32;
    cout << (log(n) / log(2));
    return 0;
}

// This code is contributed by UJJWAL BHARDWAJ

C

// C program to find log(n) using Inbuilt
// function of <math.h> library
#include <math.h>
#include <stdio.h>
int main()
{
    unsigned int n = 32;
    printf("%d", (int)log2(n));
    return 0;
}

Java

// Java program to find log(n) using Inbuilt
// function of java.util.Math library
import java.util.*;

class Gfg2
{
    public static void main(String args[])
    {
        int n = 32;
        System.out.println((int)(Math.log(n) / Math.log(2)));
    }
}

// This code is contributed by Niraj_Pandey

Python3

# Python3 program to find log(n) using Inbuilt

# Function of math library
import math

if __name__ == "__main__":
    n = 32

    print(int(math.log(n, 2)))

# This code is contributed by ukasp

C#

// C# program to find log(n) using Inbuilt
// function
using System;

class GFG{

static public void Main()
{
    int n = 32;
    Console.WriteLine((int)(Math.Log(n) / Math.Log(2)));
}
}

// This code is contributed by Ankita Saini

Javascript

<script>
//program to find log(n) using Inbuilt
// function of <math.h> library

     n = 32;
     document.write(  Math.log2(n));
//This code is contributed by simranarora5sos
</script>

Output :

5

Time complexity: O(1) 
Auxiliary space: O(1) 

Let us try an extended version of the problem.

Write a one line function Logn(n, r) which returns .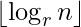 

Using Recursion

C++

// C++ program to find log(n) on arbitrary
// base using Recursion
#include <bits/stdc++.h>
using namespace std;

unsigned int Logn(unsigned int n,
                  unsigned int r)
{
    return (n > r - 1) ? 1 +
       Logn(n / r, r) : 0;
}

// Driver code
int main()
{
    unsigned int n = 256;
    unsigned int r = 3;

    cout << Logn(n, r);

    return 0;
}

// This code is contributed by UJJWAL BHARDWAJ

C

// C program to find log(n) on arbitrary base using Recursion
#include <stdio.h>

unsigned int Logn(unsigned int n, unsigned int r)
{
    return (n > r - 1) ? 1 + Logn(n / r, r) : 0;
}

int main()
{
    unsigned int n = 256;
    unsigned int r = 3;
    printf("%u", Logn(n, r));
    return 0;
}

Java

// Java program to find log(n) on
// arbitrary base using Recursion
class Gfg3
{
    static int Logn(int n, int r)
    {
        return (n > r - 1) ? 1 + Logn(n / r, r) : 0;
    }

    // Driver Code
    public static void main(String args[])
    {
        int n = 256;
        int r = 3;
        System.out.println(Logn(n, r));
    }
}

// This code is contributed by Niraj_Pandey

Python3

# Python program to find log(n) on arbitrary
# base using Recursion
def Logn(n, r):

    return  1 + Logn(n / r, r) if (n > r - 1) else 0

# Driver code
n = 256
r = 3
print(Logn(n, r))

# This code is contributed by shivanisinghss2110

C#

// C# program to find log(n) on
// arbitrary base using Recursion
using System;

public class Gfg3
{
    static int Logn(int n, int r)
    {
        return (n > r - 1) ? 1 + Logn(n / r, r) : 0;
    }

    // Driver Code
    public static void Main(String []args)
    {
        int n = 256;
        int r = 3;
        Console.WriteLine(Logn(n, r));
    }
}

// This code is contributed by gauravrajput1

Javascript

<script>
//program to find log(n) on arbitrary base using Recursion


   function Logn( n,  r)
{
    return (n > r - 1) ? 1 + Logn(n / r, r) : 0;
}

     n = 256;
     r = 3;
    document.write( Logn(n, r));
//This code is contributed by simranarora5sos
</script>

Output :

5

Time complexity: O(log n) 
Auxiliary space: O(log n) if the stack size is considered during recursion otherwise O(1)

Using inbuilt log function

We only need to use the logarithm property to find the value of log(n) on arbitrary base r. i.e., 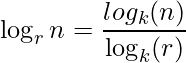where k can be any anything, which for standard log functions are either e or 10

C++

// C++ program to find log(n) on arbitrary base
// using log() library function
#include <bits/stdc++.h>
using namespace std;

unsigned int Logn(unsigned int n,
                  unsigned int r)
{
    return log(n) / log(r);
}

// Driver code
int main()
{
    unsigned int n = 256;
    unsigned int r = 3;

    cout << Logn(n, r);

    return 0;
}

// This code is contributed by UJJWAL BHARDWAJ

C

// C program to find log(n) on arbitrary base
// using log() function of maths library
#include <math.h>
#include <stdio.h>

unsigned int Logn(unsigned int n, unsigned int r)
{
    return log(n) / log(r);
}

int main()
{
    unsigned int n = 256;
    unsigned int r = 3;
    printf("%u", Logn(n, r));

    return 0;
}

Java

// Java program to find log(n) on arbitrary base
// using log() function of java.util.Math library
import java.util.*;

class Gfg4 {

    public static void main(String args[])
    {
        int n = 256;
        int r = 3;
        System.out.println((int)(Math.log(n) / Math.log(r)));
    }
}

// This code is contributed by Niraj_Pandey

Python3

# Python program to find log(n) on arbitrary base
# using log() library function
import math
def Logn(n, r):

    return math.log(n) // math.log(r)


n = 256
r = 3
print(int(Logn(n, r)))


# This code is contributed by shivanisinghss2110

C#

// C# program to find log(n) on arbitrary base
// using log() function of java.util.Math library
using System;

class Gfg4 {

    public static void Main(String []args)
    {
        int n = 256;
        int r = 3;
        Console.Write((int)(Math.Log(n) / Math.Log(r)));
    }
}

// This code is contributed by shivanisinghss2110

Javascript

<script>
// program to find log(n) on arbitrary base
// using log() function of maths library

   function  Logn( n, r)
{
    return Math.floor(Math.log(n) / Math.log(r));
}

    n = 256;
    r = 3;
    document.write( Logn(n, r));
//This code is contributed by simranarora5sos
</script>

Output :

5

Time complexity: O(1) 
Auxiliary space: O(1) 

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to contribute@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.