Problem solving on scatter matrix
Last Updated :
03 Feb, 2022
Prerequisite : Scatter Plot Matrix
We calculate Sw ( within class scatter matrix ) and SB ( between class scatter matrix ) for the available data points.
SW : To minimize variability within a class, inner class scatter.
SB : To increase between class variability, between class scatter.

scatter plot of the points
X1 = (y1, y2) ={ (2,2), (1,2), (1,2), (1,2), (2,2) }
X2 = (y1,y2) ={ (9, 10), (6,8), (9,5), (8,7), (10,8) }
Within class scatter matrix :
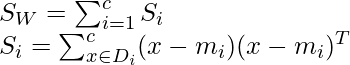
Si is the class specific covariance matrix.
mi is the mean of individual class
Mean computation :
We calculate the mean for each of the points present in the class. Here mean is the total sum of observations divided by the number of observations, we require this mean for calculating the covariance of the matrix.
![Rendered by QuickLaTeX.com m_1 = [\frac{2+1+1+1+2}{5} , \frac{2+2+2+2+2}{5} ] \\ = [1.4,2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dcd317c58deb7a4375424219e3e3353d_l3.png)
![Rendered by QuickLaTeX.com m_2 = [\frac{9+6+9+8+10}{5} , \frac{10+8+5+7+8}{5} ] \\ = [8.4,7.6]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3c84b6f2af4933ef396b0fbf967a73cd_l3.png)
Covariance matrix computation :
We subtract the mean value from each of the observation and then we calculate the average after performing the matrix multiplication with the transpose of the matrix.
Class specific covariance for the first class :
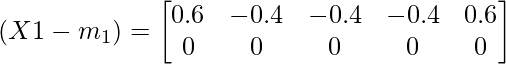
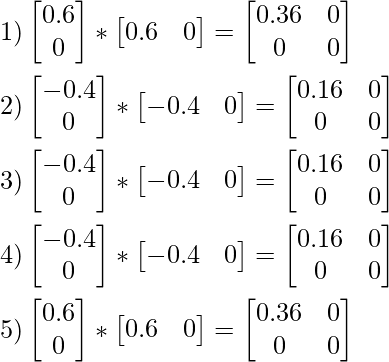
Averaging values from 1,2,3,4 and 5.
We calculate the sum of all the values for each element in the matrix for S1 and divide by the number of the observation which in the present computation is 5.
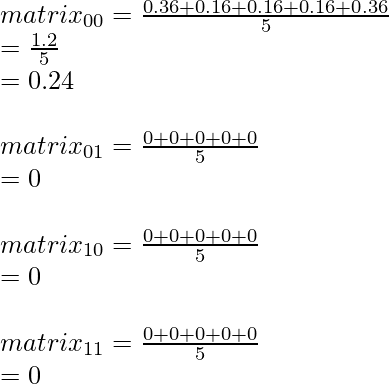
Therefore S1 is :
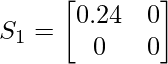
Class specific covariance for the second class :
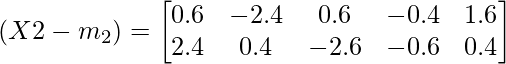
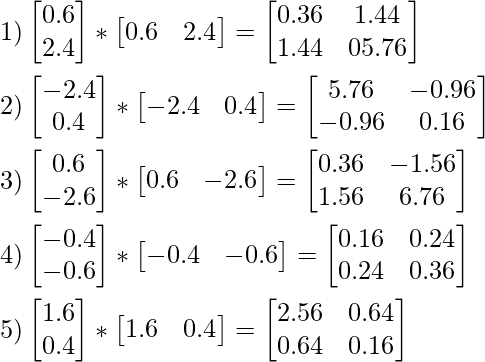
Averaging values from 1,2,3,4 and 5
we calculate the sum of all the values for each element in the matrix for S2 and divide by the number of the observation which in the present computation is 5.
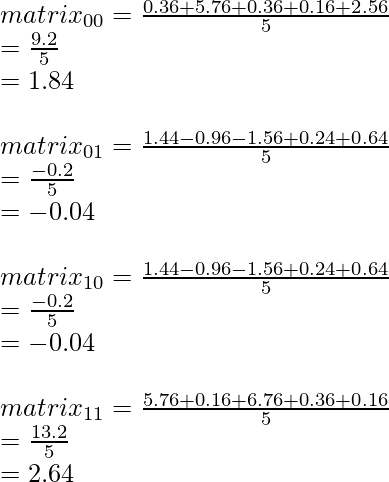
Therefore S2 is :
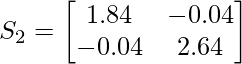
Within class scatter matrix Sw :
SW = S1 + S2
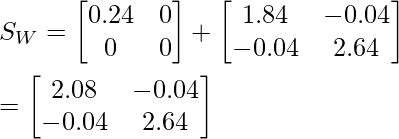
Between class scatter matrix SB :
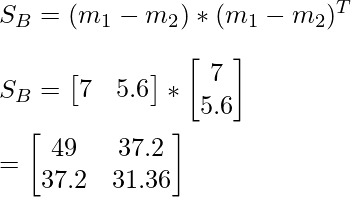
Total scatter matrix :
ST = SB + SW
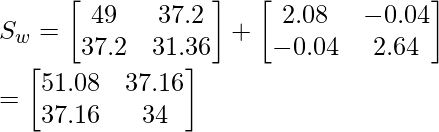
Therefore we have calculated between class scatter matrix and within class scatter matrix for the available data points.
We make use of these computations in feature extraction , where the main goal is to increase the distance between the class in the projection of points and decrease the distance between the points within the class in the projection. Here we aim at generating data projection at the required dimension.
Share your thoughts in the comments
Please Login to comment...