Print all ways to break a string in bracket form

Given a string, find all ways to break the given string in bracket form. Enclose each substring within a parenthesis.

Examples: 

Input : abc
Output: (a)(b)(c)
        (a)(bc)
        (ab)(c)
        (abc)


Input : abcd
Output : (a)(b)(c)(d)
         (a)(b)(cd)
         (a)(bc)(d)
         (a)(bcd)
         (ab)(c)(d)
         (ab)(cd)
         (abc)(d)
         (abcd)

We strongly recommend you to minimize your browser and try this yourself first.

The idea is to use recursion. We maintain two parameters – index of the next character to be processed and the output string so far. We start from index of next character to be processed, append substring formed by unprocessed string to the output string and recurse on remaining string until we process the whole string. We use std::substr to form the output string. substr(pos, n) returns a substring of length n that starts at position pos of current string.

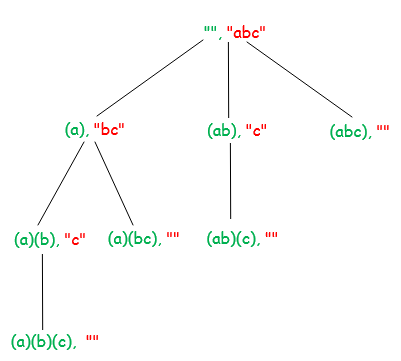
Below diagram shows recursion tree for input string “abc”. Each node on the diagram shows processed string (marked by green) and unprocessed string (marked by red).

Below is the implementation of the above idea

C++

// C++ Program to find all combinations of Non-
// overlapping substrings formed from given
// string
#include <iostream>
using namespace std;

// find all combinations of non-overlapping
// substrings formed by input string str
// index – index of the next character to
//          be processed
// out - output string so far
void findCombinations(string str, int index, string out)
{
    if (index == str.length())
        cout << out << endl;

    for (int i = index; i < str.length(); i++)
    {
        // append substring formed by str[index,
        // i] to output string
        findCombinations(
            str,
            i + 1,
            out + "(" + str.substr(index, i + 1 - index)
                + ")");
    }
}

// Driver Code
int main()
{
    // input string
    string str = "abcd";

    findCombinations(str, 0, "");

    return 0;
}

Java

// Java program to find all combinations of Non-
// overlapping substrings formed from given
// string

class GFG
{
    // find all combinations of non-overlapping
    // substrings formed by input string str
    static void findCombinations(String str, int index,
                                 String out)
    {
        if (index == str.length())
            System.out.println(out);

        for (int i = index; i < str.length(); i++)

            // append substring formed by str[index,
            // i] to output string
            findCombinations(str, i + 1, out +
                "(" + str.substring(index, i+1) + ")" );
    }

    // Driver Code
    public static void main (String[] args)
    {
        // input string
        String str = "abcd";
        findCombinations(str, 0, "");
    }
}

// Contributed by Pramod Kumar

Python3

# Python3 Program to find all combinations of Non-
# overlapping substrings formed from given
# string

# find all combinations of non-overlapping
# substrings formed by input string str
# index – index of the next character to
#          be processed
# out - output string so far
def findCombinations(string, index, out):
    if index == len(string):
        print(out)

    for i in range(index, len(string), 1):

        # append substring formed by str[index,
        # i] to output string
        findCombinations(string, i + 1, out + "(" +
                         string[index:i + 1] + ")")

# Driver Code
if __name__ == "__main__":

    # input string
    string = "abcd"
    findCombinations(string, 0, "")

# This code is contributed by
# sanjeev2552

C#

// C# program to find all combinations
// of Non-overlapping substrings formed
// from given string
using System;

class GFG {
    // find all combinations of non-overlapping
    // substrings formed by input string str
    public static void
    findCombinations(string str, int index, string @out)
    {
        if (index == str.Length) {
            Console.WriteLine(@out);
        }

        for (int i = index; i < str.Length; i++) {

            // append substring formed by
            // str[index, i] to output string
            findCombinations(
                str, i + 1,
                @out + "("
                    + str.Substring(index, (i + 1) - index)
                    + ")");
        }
    }

    // Driver Code
    public static void Main(string[] args)
    {
        // input string
        string str = "abcd";
        findCombinations(str, 0, "");
    }
}

// This code is contributed by Shrikant13

Javascript

// Javascript program for the above approach

// find all combinations of non-overlapping
// substrings formed by input string str
// index – index of the next character to
//          be processed
// out - output string so far
function findCombinations(string, index, out) {
  if (index == string.length) {
    console.log(out);
  }

  for (let i = index; i < string.length; i++) {
    // append substring formed by str[index,
    // i] to output string
    findCombinations(string, i + 1, out + "(" + string.substring(index, i + 1) + ")");
  }
}

// Driver Code
const string = "abcd";
findCombinations(string, 0, "");


// contributed by adityasharmadev01

Output

(a)(b)(c)(d)
(a)(b)(cd)
(a)(bc)(d)
(a)(bcd)
(ab)(c)(d)
(ab)(cd)
(abc)(d)
(abcd)

Time Complexity: O(N²)
Auxiliary Space: O(N²)

If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.