Print all nodes that are at distance k from a leaf node

Given a Binary Tree and a positive integer K, print all nodes that are distance K from a leaf node. Here K distance from a leaf means K levels higher than a leaf node. For example, if K is more than the height of the Binary Tree, then nothing should be printed. 

Examples:

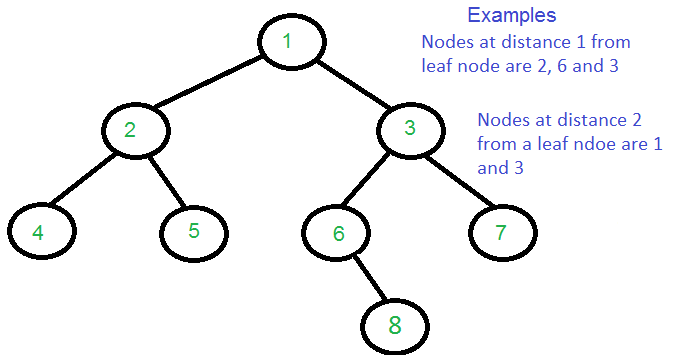
Approach: To solve the problem follow the below idea: 

We can store the nodes in the path of our recursion and whenever we reach a leaf node, then print the Kth node in the saved path

Follow the below steps to solve the problem:

• Traverse the tree and keep storing all ancestors till we hit a leaf node. 
• When we reach a leaf node, we print the ancestor at distance K using the values stored in the array. 
• We also need to keep track of nodes that are already printed as output. For that, we use a boolean array visited[]

Below is the implementation of the above approach:

C++

/* C++ Program to print all nodes
which are at distance k from a leaf */
#include <iostream>
using namespace std;
#define MAX_HEIGHT 10000

struct Node {
    int key;
    Node *left, *right;
};

/* utility that allocates a new Node with the given key  */
Node* newNode(int key)
{
    Node* node = new Node;
    node->key = key;
    node->left = node->right = NULL;
    return (node);
}

/* This function prints all nodes that are distance k from a
   leaf node path[] --> Store ancestors of a node visited[]
   --> Stores true if a node is printed as output.  A node
   may be k
                 distance away from many leaves, we want to
   print it once */
void kDistantFromLeafUtil(Node* node, int path[],
                          bool visited[], int pathLen,
                          int k)
{
    // Base case
    if (node == NULL)
        return;

    /* append this Node to the path array */
    path[pathLen] = node->key;
    visited[pathLen] = false;
    pathLen++;

    /* it's a leaf, so print the ancestor at distance k only
       if the ancestor is not already printed  */
    if (node->left == NULL && node->right == NULL
        && pathLen - k - 1 >= 0
        && visited[pathLen - k - 1] == false) {
        cout << path[pathLen - k - 1] << " ";
        visited[pathLen - k - 1] = true;
        return;
    }

    /* If not leaf node, recur for left and right subtrees
     */
    kDistantFromLeafUtil(node->left, path, visited, pathLen,
                         k);
    kDistantFromLeafUtil(node->right, path, visited,
                         pathLen, k);
}

/* Given a binary tree and a number k, print all nodes that
   are k distant from a leaf*/
void printKDistantfromLeaf(Node* node, int k)
{
    int path[MAX_HEIGHT];
    bool visited[MAX_HEIGHT] = { false };
    kDistantFromLeafUtil(node, path, visited, 0, k);
}

/* Driver code*/
int main()
{
    // Let us create binary tree
    // given in the above example
    Node* root = newNode(1);
    root->left = newNode(2);
    root->right = newNode(3);
    root->left->left = newNode(4);
    root->left->right = newNode(5);
    root->right->left = newNode(6);
    root->right->right = newNode(7);
    root->right->left->right = newNode(8);

    cout << "Nodes at distance 2 are: ";
    printKDistantfromLeaf(root, 2);

    return 0;
}

Java

// Java program to print all nodes at a distance k from leaf
// A binary tree node
class Node {
    int data;
    Node left, right;

    Node(int item)
    {
        data = item;
        left = right = null;
    }
}

class BinaryTree {
    Node root;

    /* This function prints all nodes that are distance k
     from a leaf node path[] --> Store ancestors of a node
     visited[] --> Stores true if a node is printed as
     output.  A node may be k distance away from many
     leaves, we want to print it once */
    void kDistantFromLeafUtil(Node node, int path[],
                              boolean visited[],
                              int pathLen, int k)
    {
        // Base case
        if (node == null)
            return;

        /* append this Node to the path array */
        path[pathLen] = node.data;
        visited[pathLen] = false;
        pathLen++;

        /* it's a leaf, so print the ancestor at distance k
         only if the ancestor is not already printed  */
        if (node.left == null && node.right == null
            && pathLen - k - 1 >= 0
            && visited[pathLen - k - 1] == false) {
            System.out.print(path[pathLen - k - 1] + " ");
            visited[pathLen - k - 1] = true;
            return;
        }

        /* If not leaf node, recur for left and right
         * subtrees */
        kDistantFromLeafUtil(node.left, path, visited,
                             pathLen, k);
        kDistantFromLeafUtil(node.right, path, visited,
                             pathLen, k);
    }

    /* Given a binary tree and a number k, print all nodes
     that are k distant from a leaf*/
    void printKDistantfromLeaf(Node node, int k)
    {
        int path[] = new int[1000];
        boolean visited[] = new boolean[1000];
        kDistantFromLeafUtil(node, path, visited, 0, k);
    }

    // Driver code
    public static void main(String args[])
    {
        BinaryTree tree = new BinaryTree();

        /* Let us construct the tree shown in above diagram
         */
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(6);
        tree.root.right.right = new Node(7);
        tree.root.right.left.right = new Node(8);

        System.out.print(" Nodes at distance 2 are : ");
        tree.printKDistantfromLeaf(tree.root, 2);
    }
}

// This code has been contributed by Mayank Jaiswal

Python3

# Program to print all nodes which are at
# distance k from a leaf

# utility that allocates a new Node with
# the given key


class newNode:
    def __init__(self, key):
        self.key = key
        self.left = self.right = None

# This function prints all nodes that
# are distance k from a leaf node
# path[] -. Store ancestors of a node
# visited[] -. Stores true if a node is
# printed as output. A node may be k distance
# away from many leaves, we want to print it once


def kDistantFromLeafUtil(node, path, visited,
                         pathLen, k):

    # Base case
    if (node == None):
        return

    # append this Node to the path array
    path[pathLen] = node.key
    visited[pathLen] = False
    pathLen += 1

    # it's a leaf, so print the ancestor at
    # distance k only if the ancestor is
    # not already printed
    if (node.left == None and node.right == None and
        pathLen - k - 1 >= 0 and
            visited[pathLen - k - 1] == False):
        print(path[pathLen - k - 1], end=" ")
        visited[pathLen - k - 1] = True
        return

    # If not leaf node, recur for left
    # and right subtrees
    kDistantFromLeafUtil(node.left, path,
                         visited, pathLen, k)
    kDistantFromLeafUtil(node.right, path,
                         visited, pathLen, k)

# Given a binary tree and a number k,
# print all nodes that are k distant from a leaf


def printKDistantfromLeaf(node, k):
    global MAX_HEIGHT
    path = [None] * MAX_HEIGHT
    visited = [False] * MAX_HEIGHT
    kDistantFromLeafUtil(node, path, visited, 0, k)


# Driver Code
MAX_HEIGHT = 10000

# Let us create binary tree given in
# the above example
root = newNode(1)
root.left = newNode(2)
root.right = newNode(3)
root.left.left = newNode(4)
root.left.right = newNode(5)
root.right.left = newNode(6)
root.right.right = newNode(7)
root.right.left.right = newNode(8)

print("Nodes at distance 2 are:", end=" ")
printKDistantfromLeaf(root, 2)

# This code is contributed by pranchalK

C#

using System;

// C# program to print all nodes at a distance k from leaf
// A binary tree node
public class Node {
    public int data;
    public Node left, right;

    public Node(int item)
    {
        data = item;
        left = right = null;
    }
}

public class BinaryTree {
    public Node root;

    /* This function prints all nodes that are distance k
     from a leaf node path[] --> Store ancestors of a node
     visited[] --> Stores true if a node is printed as
     output.  A node may be k distance away from many
     leaves, we want to print it once */
    public virtual void
    kDistantFromLeafUtil(Node node, int[] path,
                         bool[] visited, int pathLen, int k)
    {
        // Base case
        if (node == null) {
            return;
        }

        /* append this Node to the path array */
        path[pathLen] = node.data;
        visited[pathLen] = false;
        pathLen++;

        /* it's a leaf, so print the ancestor at distance k
         only if the ancestor is not already printed  */
        if (node.left == null && node.right == null
            && pathLen - k - 1 >= 0
            && visited[pathLen - k - 1] == false) {
            Console.Write(path[pathLen - k - 1] + " ");
            visited[pathLen - k - 1] = true;
            return;
        }

        /* If not leaf node, recur for left and right
         * subtrees */
        kDistantFromLeafUtil(node.left, path, visited,
                             pathLen, k);
        kDistantFromLeafUtil(node.right, path, visited,
                             pathLen, k);
    }

    /* Given a binary tree and a number k, print all nodes
     that are k distant from a leaf*/
    public virtual void printKDistantfromLeaf(Node node,
                                              int k)
    {
        int[] path = new int[1000];
        bool[] visited = new bool[1000];
        kDistantFromLeafUtil(node, path, visited, 0, k);
    }

    // Driver program to test the above functions
    public static void Main(string[] args)
    {
        BinaryTree tree = new BinaryTree();

        /* Let us construct the tree shown in above diagram
         */
        tree.root = new Node(1);
        tree.root.left = new Node(2);
        tree.root.right = new Node(3);
        tree.root.left.left = new Node(4);
        tree.root.left.right = new Node(5);
        tree.root.right.left = new Node(6);
        tree.root.right.right = new Node(7);
        tree.root.right.left.right = new Node(8);

        Console.Write(" Nodes at distance 2 are : ");
        tree.printKDistantfromLeaf(tree.root, 2);
    }
}

// This code is contributed by Shrikant13

Javascript

<script>

    // JavaScript program to print all
    // nodes at a distance k from leaf
    // A binary tree node

    class Node
    {
        constructor(item) {
           this.left = null;
           this.right = null;
           this.data = item;
        }
    }

    let root;

    /* This function prints all nodes that
       are distance k from a leaf node
       path[] --> Store ancestors of a node
       visited[] --> Stores true if a node is
       printed as output.  A node may
       be k distance away from many leaves,
       we want to print it once */
    function kDistantFromLeafUtil(node, path, visited, pathLen, k)
    {
        // Base case
        if (node == null)
            return;

        /* append this Node to the path array */
        path[pathLen] = node.data;
        visited[pathLen] = false;
        pathLen++;

        /* it's a leaf, so print the ancestor at distance k only
         if the ancestor is not already printed  */
        if (node.left == null && node.right == null
            && (pathLen - k - 1) >= 0 &&
            visited[pathLen - k - 1] == false) {
            document.write(path[pathLen - k - 1] + " ");
            visited[pathLen - k - 1] = true;
            return;
        }

        /* If not leaf node, recur for left and right subtrees */
        kDistantFromLeafUtil(node.left, path, visited, pathLen, k);
        kDistantFromLeafUtil(node.right, path, visited, pathLen, k);
    }

    /* Given a binary tree and a number k, print all nodes that are k
     distant from a leaf*/
    function printKDistantfromLeaf(node, k)
    {
        let path = new Array(1000);
        path.fill(0);
        let visited = new Array(1000);
        visited.fill(false);
        kDistantFromLeafUtil(node, path, visited, 0, k);
    }

    /* Let us construct the tree shown in above diagram */
    root = new Node(1);
    root.left = new Node(2);
    root.right = new Node(3);
    root.left.left = new Node(4);
    root.left.right = new Node(5);
    root.right.left = new Node(6);
    root.right.right = new Node(7);
    root.right.left.right = new Node(8);

    document.write(" Nodes at distance 2 are : ");
    printKDistantfromLeaf(root, 2);

</script>

Output

Nodes at distance 2 are: 1 3 

Time Complexity: O(N)
Auxiliary Space: O(N)