Print All Permutations of an Array
Last Updated :
03 Nov, 2023
Given vector nums, the task is to print all the possible permutations of the given vector using backtracking
Examples:
Input: nums[] = {1, 2, 3}
Output: {1, 2, 3}, {1, 3, 2}, {2, 1, 3}, {2, 3, 1}, {3, 2, 1}, {3, 1, 2}
Explanation: There are 6 possible permutations
Input: nums[] = {1, 3}
Output: {1, 3}, {3, 1}
Explanation: There are 2 possible permutations
Approach: The task can be solved with the help of backtracking. A similar article for better understanding is here: Print all permutations of a given string
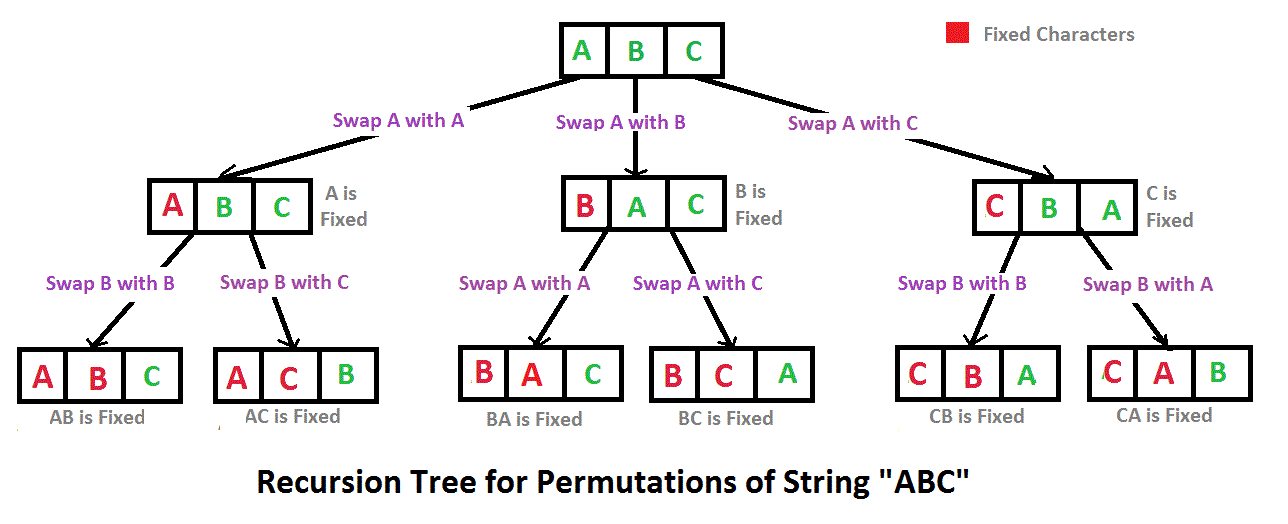
Below is the implementation of the above code:
C++
#include <bits/stdc++.h>
using namespace std;
void swap(int& x, int& y)
{
int temp = x;
x = y;
y = temp;
}
void permutations(vector<vector<int> >& res,
vector<int> nums, int l, int h)
{
if (l == h) {
res.push_back(nums);
return;
}
for (int i = l; i <= h; i++) {
swap(nums[l], nums[i]);
permutations(res, nums, l + 1, h);
swap(nums[l], nums[i]);
}
}
vector<vector<int> > permute(vector<int>& nums)
{
vector<vector<int> > res;
int x = nums.size() - 1;
permutations(res, nums, 0, x);
return res;
}
int main()
{
vector<int> nums = { 1, 2, 3 };
vector<vector<int> > res = permute(nums);
for (auto x : res) {
for (auto y : x) {
cout << y << " ";
}
cout << endl;
}
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.Arrays;
public class GFG
{
static void swap(int nums[], int l, int i)
{
int temp = nums[l];
nums[l] = nums[i];
nums[i] = temp;
}
static void permutations(ArrayList<int[]> res,
int[] nums, int l, int h)
{
if (l == h) {
res.add(Arrays.copyOf(nums, nums.length));
return;
}
for (int i = l; i <= h; i++) {
swap(nums, l, i);
permutations(res, nums, l + 1, h);
swap(nums, l, i);
}
}
static ArrayList<int[]> permute(int[] nums)
{
ArrayList<int[]> res = new ArrayList<int[]>();
int x = nums.length - 1;
permutations(res, nums, 0, x);
return res;
}
public static void main(String[] args)
{
int[] nums = { 1, 2, 3 };
ArrayList<int[]> res = permute(nums);
for (int[] x : res) {
for (int y : x) {
System.out.print(y + " ");
}
System.out.println();
}
}
}
|
Python3
def permutations(res, nums, l, h) :
if (l == h) :
res.append(nums);
for i in range(len(nums)):
print(nums[i], end=' ');
print('')
return;
for i in range(l, h + 1):
temp = nums[l];
nums[l] = nums[i];
nums[i] = temp;
permutations(res, nums, l + 1, h);
temp = nums[l];
nums[l] = nums[i];
nums[i] = temp;
def permute(nums):
x = len(nums) - 1;
res = [];
permutations(res, nums, 0, x);
return res;
nums = [ 1, 2, 3 ];
res = permute(nums);
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static void swap(int[] nums, int l, int i)
{
int temp = nums[l];
nums[l] = nums[i];
nums[i] = temp;
}
static void permutations(List<int[]> res, int[] nums, int l, int h)
{
if (l == h)
{
res.Add((int[])nums.Clone());
return;
}
for (int i = l; i <= h; i++)
{
swap(nums, l, i);
permutations(res, nums, l + 1, h);
swap(nums, l, i);
}
}
static List<int[]> permute(int[] nums)
{
List<int[]> res = new List<int[]>();
int x = nums.Length - 1;
permutations(res, nums, 0, x);
return res;
}
static void Main(string[] args)
{
int[] nums = { 1, 2, 3 };
List<int[]> res = permute(nums);
foreach (int[] x in res)
{
foreach (int y in x)
{
Console.Write(y + " ");
}
Console.WriteLine();
}
}
}
|
Javascript
<script>
function permutations(res, nums, l, h)
{
if (l == h)
{
res.push(nums);
for(let i = 0; i < nums.length; i++)
document.write(nums[i] + ' ');
document.write('<br>')
return;
}
for(let i = l; i <= h; i++)
{
let temp = nums[l];
nums[l] = nums[i];
nums[i] = temp;
permutations(res, nums, l + 1, h);
temp = nums[l];
nums[l] = nums[i];
nums[i] = temp;
}
}
function permute(nums)
{
let x = nums.length - 1;
let res = [];
permutations(res, nums, 0, x);
return res;
}
let nums = [ 1, 2, 3 ];
let res = permute(nums);
</script>
|
Output
1 2 3
1 3 2
2 1 3
2 3 1
3 2 1
3 1 2
Time Complexity: O(N*N!) Note that there are N! permutations and it requires O(N) time to print a permutation.
Auxiliary Space: O(r – l)
Share your thoughts in the comments
Please Login to comment...