Perfect Square factors of a Number
Last Updated :
29 Oct, 2023
Given an integer N, the task is to find the number of factors of N which are a perfect square.
Examples:
Input: N = 100
Output: 4
Explanation:
There are four factors of
100 (1, 4, 25, 100) that are perfect square.
Input: N = 900
Output: 8
Explanation:
There are eight factors of 900 (1, 4, 9, 25, 36, 100, 225, 900) that are perfect square.
Naive Approach: The simplest approach to solve this problem is to find all possible factors of the given number N and for each factor, check if the factor is a perfect square or not. For every factor found to be so, increase count. Print the final count.
Time Complexity: O(N)
Auxiliary Space: O(1)
Efficient Approach:
The following observations need to be made to optimize the above approach:
The number of factors for a number is given by:
Factors of N = (1 + a1)*(1 + a2)*(1 + a3)*..*(1 + an)
where a1, a2, a3, …, an are the count of distinct prime factors of N.
In a perfect square, the count of distinct prime factors must be divisible by 2. Therefore, the count of factors that are a perfect square is given by:
Factors of N that are perfect square = (1 + a1/2)*(1 + a2/2)*…*(1 + an/2) where a1, a2, a3, …, an are the count of distinct prime factors of N.
Illustration:
The prime factors of N = 100 are 2, 2, 5, 5.
Therefore, the number of factors that are perfect square are (1 + 2/2) * (1 + 2/2) = 4.
The factors are 1, 4, 25, 100.
Therefore, find the count of prime factors and apply the above formula to find the count of factors that are a perfect square.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int noOfFactors(int N)
{
if (N == 1)
return 1;
int count = 0;
int ans = 1;
while (N % 2 == 0) {
count++;
N = N / 2;
}
ans *= (count / 2 + 1);
for (int i = 3;
i * i <= N; i = i + 2) {
count = 0;
while (N % i == 0) {
count++;
N = N / i;
}
ans *= (count / 2 + 1);
}
return ans;
}
int main()
{
int N = 100;
cout << noOfFactors(N);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int noOfFactors(int N)
{
if (N == 1)
return 1;
int count = 0;
int ans = 1;
while (N % 2 == 0)
{
count++;
N = N / 2;
}
ans *= (count / 2 + 1);
for(int i = 3; i * i <= N; i = i + 2)
{
count = 0;
while (N % i == 0)
{
count++;
N = N / i;
}
ans *= (count / 2 + 1);
}
return ans;
}
public static void main(String[] args)
{
int N = 100;
System.out.print(noOfFactors(N));
}
}
|
Python3
def noOfFactors(N):
if (N == 1):
return 1
count = 0
ans = 1
while (N % 2 == 0):
count += 1
N = N // 2
ans *= (count // 2 + 1)
i = 3
while i * i <= N:
count = 0
while (N % i == 0):
count += 1
N = N // i
ans *= (count // 2 + 1)
i += 2
return ans
if __name__ == "__main__":
N = 100
print(noOfFactors(N))
|
C#
using System;
class GFG{
static int noOfFactors(int N)
{
if (N == 1)
return 1;
int count = 0;
int ans = 1;
while (N % 2 == 0)
{
count++;
N = N / 2;
}
ans *= (count / 2 + 1);
for(int i = 3; i * i <= N; i = i + 2)
{
count = 0;
while (N % i == 0)
{
count++;
N = N / i;
}
ans *= (count / 2 + 1);
}
return ans;
}
public static void Main(String[] args)
{
int N = 100;
Console.Write(noOfFactors(N));
}
}
|
Javascript
<script>
function noOfFactors(N)
{
if (N == 1)
return 1;
let count = 0;
let ans = 1;
while (N % 2 == 0)
{
count++;
N = N / 2;
}
ans *= (count / 2 + 1);
for(let i = 3; i * i <= N; i = i + 2)
{
count = 0;
while (N % i == 0)
{
count++;
N = N / i;
}
ans *= (count / 2 + 1);
}
return ans;
}
let N = 100;
document.write(noOfFactors(N));
</script>
|
Time Complexity: 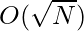
Space Complexity: O(1)
Perfect Square factors of a Number using inbuilt function
In this approach, we will iterate through all the factors of the given number and check if each factor is a perfect square or not. If a factor is a perfect square, we will increment the count.
- Define a function count_perfect_squares_factors1 that takes a single parameter N.
- Initialize a variable count to 0 to keep track of the number of perfect square factors.
- Loop through all the numbers from 1 to N using the range function.
- Check if the current number i is a factor of N and a perfect square using the N % i == 0 and math.sqrt(i) == int(math.sqrt(i)) conditions, respectively.
- If i is a perfect square factor, increment count.
- Return the final value of count.
- Print the result of calling count_perfect_squares_factors1 with some example inputs to verify that the function works as expected.
C++
#include <cmath>
#include <iostream>
int count_perfect_squares_factors1(int N)
{
int count = 0;
for (int i = 1; i <= N; ++i) {
if (N % i == 0
&& std::sqrt(i)
== static_cast<int>(std::sqrt(i))) {
count++;
}
}
return count;
}
int main()
{
std::cout << count_perfect_squares_factors1(100)
<< std::endl;
std::cout << count_perfect_squares_factors1(900)
<< std::endl;
return 0;
}
|
Java
import java.util.Scanner;
public class Main {
static int countPerfectSquareFactors(int N)
{
int count = 0;
for (int i = 1; i <= N; ++i) {
if (N % i == 0
&& Math.sqrt(i) == (int)Math.sqrt(i)) {
count++;
}
}
return count;
}
public static void main(String[] args)
{
System.out.println(
countPerfectSquareFactors(100));
System.out.println(
countPerfectSquareFactors(900));
}
}
|
Python3
import math
def count_perfect_squares_factors1(N):
count = 0
for i in range(1, N+1):
if N % i == 0 and math.sqrt(i) == int(math.sqrt(i)):
count += 1
return count
print(count_perfect_squares_factors1(100))
print(count_perfect_squares_factors1(900))
|
C#
using System;
class Program {
static int CountPerfectSquareFactors(int N)
{
int count = 0;
for (int i = 1; i <= N; ++i) {
if (N % i == 0
&& Math.Sqrt(i) == (int)Math.Sqrt(i)) {
count++;
}
}
return count;
}
static void Main()
{
Console.WriteLine(CountPerfectSquareFactors(100));
Console.WriteLine(CountPerfectSquareFactors(900));
}
}
|
Javascript
function countPerfectSquaresFactors(N) {
let count = 0;
for (let i = 1; i <= N; i++) {
if (N % i === 0 && Math.sqrt(i) === Math.floor(Math.sqrt(i))) {
count++;
}
}
return count;
}
console.log(countPerfectSquaresFactors(100));
console.log(countPerfectSquaresFactors(900));
|
Time complexity: O(N)
Space complexity: O(1)
Share your thoughts in the comments
Please Login to comment...