Overview of Graph, Trie, Segment Tree and Suffix Tree Data Structures
Last Updated :
09 Feb, 2023
Introduction:
- Graph: A graph is a collection of vertices (nodes) and edges that represent relationships between the vertices. Graphs are used to model and analyze networks, such as social networks or transportation networks.
- Trie: A trie, also known as a prefix tree, is a tree-like data structure that stores a collection of strings. It is used for efficient searching and retrieval of strings, especially in the case of a large number of strings.
- Segment Tree: A segment tree is a tree-like data structure that stores information about ranges of values. It is used for range queries and range updates, such as finding the sum of an array or finding the minimum or maximum value in an array.
- Suffix Tree: A suffix tree is a tree-like data structure that stores all suffixes of a given string. It is used for efficient string search and pattern matching, such as finding the longest repeated substring or the longest common substring.
We have discussed below data structures in the previous two sets. Set 1: Overview of Array, Linked List, Queue and Stack. Set 2: Overview of Binary Tree, BST, Heap and Hash. 9. Graph 10. Trie 11. Segment Tree 12. Suffix Tree
Graph: Graph is a data structure that consists of the following two components:
- A finite set of vertices is also called nodes.
- A finite set of ordered pairs of the form (u, v) is called an edge. The pair is ordered because (u, v) is not the same as (v, u) in the case of a directed graph(di-graph). The pair of forms (u, v) indicates that there is an edge from vertex u to vertex v. The edges may contain weight/value/cost.
V -> Number of Vertices. E -> Number of Edges. The graph can be classified on the basis of many things, below are the two most common classifications :
- Direction: Undirected Graph: The graph in which all the edges are bidirectional.Directed Graph: The graph in which all the edges are unidirectional.
- Weight: Weighted Graph: The Graph in which weight is associated with the edges.Unweighted Graph: The Graph in which there is no weight associated with the edges.
Algorithm to implement graph –
The general algorithmic steps to implement a graph data structure:
- Create a class for the graph: Start by creating a class that represents the graph data structure. This class should contain variables or data structures to store information about the vertices and edges in the graph.
- Represent vertices: Choose a data structure to represent the vertices in the graph. For example, you could use an array, linked list, or dictionary.
- Represent edges: Choose a data structure to represent the edges in the graph. For example, you could use an adjacency matrix or an adjacency list.
- Add vertices: Implement a method to add vertices to the graph. You should store information about the vertex, such as its name or identifier.
- Add edges: Implement a method to add edges between vertices in the graph. You should store information about the edge, such as its weight or direction.
- Search for vertices: Implement a method to search for a specific vertex in the graph.
- Search for edges: Implement a method to search for a specific edge in the graph.
- Remove vertices: Implement a method to remove vertices from the graph.
- Remove edges: Implement a method to remove edges from the graph.
- Traverse the graph: Implement a method to traverse the graph and visit each vertex. You could use algorithms like depth-first search or breadth-first search.
This algorithm provides a basic structure for implementing a graph data structure in any programming language. You can adjust the implementation to meet the specific needs of your application.
Graphs can be represented in many ways, below are the two most common representations: Let us take the below example graph to see two representations of the graph.
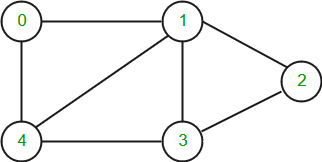
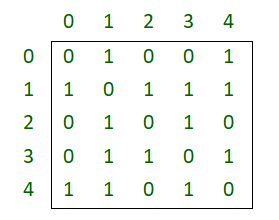
Adjacency Matrix Representation of the above graph

Adjacency List Representation of the above Graph
Time Complexities in case of Adjacency Matrix :
Traversal :(By BFS or DFS) O(V^2)
Space : O(V^2)
Time Complexities in case of Adjacency List :
Traversal :(By BFS or DFS) O(V + E)
Space : O(V+E)
Examples: The most common example of the graph is to find the shortest path in any network. Used in google maps or bing. Another common use application of graphs is social networking websites where the friend suggestion depends on the number of intermediate suggestions and other things.
Trie
Trie is an efficient data structure for searching words in dictionaries, search complexity with Trie is linear in terms of word (or key) length to be searched. If we store keys in a binary search tree, a well-balanced BST will need time proportional to M * log N, where M is the maximum string length and N is the number of keys in the tree. Using trie, we can search the key in O(M) time. So it is much faster than BST. Hashing also provides word search in O(n) time on average. But the advantages of Trie are there are no collisions (like hashing) so the worst-case time complexity is O(n). Also, the most important thing is Prefix Search. With Trie, we can find all words beginning with a prefix (This is not possible with Hashing). The only problem with Tries is they require a lot of extra space. Tries are also known as radix trees or prefix trees.
The Trie structure can be defined as follows :
struct trie_node
{
int value; /* Used to mark leaf nodes */
trie_node_t *children[ALPHABET_SIZE];
};
root
/ \ \
t a b
| | |
h n y
| | \ |
e s y e
/ | |
i r w
| | |
r e e
|
r
The leaf nodes are in blue.
Insert time : O(M) where M is the length of the string.
Search time : O(M) where M is the length of the string.
Space : O(ALPHABET_SIZE * M * N) where N is number of
keys in trie, ALPHABET_SIZE is 26 if we are
only considering upper case Latin characters.
Deletion time: O(M)
Algorithm to implement tree –
Here is a general algorithmic step to implement a tree data structure:
- Create a class for the tree: Start by creating a class that represents the tree data structure. This class should contain variables or data structures to store information about the nodes in the tree.
- Represent nodes: Choose a data structure to represent the nodes in the tree. For example, you could use an array, linked list, or dictionary.
- Add nodes: Implement a method to add nodes to the tree. You should store information about the node, such as its value or identifier.
- Add relationships: Implement a method to add relationships between nodes in the tree. For example, you could define a parent-child relationship between nodes.
- Search for nodes: Implement a method to search for a specific node in the tree.
- Remove nodes: Implement a method to remove nodes from the tree.
- Traverse the tree: Implement a method to traverse the tree and visit each node. You could use algorithms like in-order, pre-order, or post-order traversal.
This algorithm provides a basic structure for implementing a tree data structure in any programming language. You can adjust the implementation to meet the specific needs of your application.
Example: The most common use of Tries is to implement dictionaries due to prefix search capability. Tries are also well suited for implementing approximate matching algorithms, including those used in spell checking. It is also used for searching Contact from Mobile Contact list OR Phone Directory.
Segment Tree
This data structure is usually implemented when there are a lot of queries on a set of values. These queries involve minimum, maximum, sum, .. etc on an input range of a given set. Queries also involve updating values in the given set. Segment Trees are implemented using an array. 
Construction of segment tree : O(N)
Query : O(log N)
Update : O(log N)
Space : O(N) [Exact space = 2*N-1]
Example: It is used when we need to find the Maximum/Minimum/Sum/Product of numbers in a range.
Suffix Tree
The suffix tree is mainly used to search for a pattern in a text. The idea is to preprocess the text so that the search operation can be done in time linear in terms of pattern length. The pattern searching algorithms like KMP, Z, etc take time proportional to text length. This is really a great improvement because the length of the pattern is generally much smaller than the text. Imagine we have stored the complete work of William Shakespeare and preprocessed it. You can search any string in the complete work in time just proportional to the length of the pattern. But using Suffix Tree may not be a good idea when text changes frequently like text editor, etc. A suffix tree is a compressed trie of all suffixes, so the following are very abstract steps to build a suffix tree from given text. 1) Generate all suffixes of the given text. 2) Consider all suffixes as individual words and build a compressed trie.

Example: Used to find all occurrences of the pattern in a string. It is also used to find the longest repeated substring (when the text doesn’t change often), the longest common substring and the longest palindrome in a string.
Graphs:
Advantages:
- Represent complex relationships: Graphs can be used to represent complex relationships between objects, making it a suitable data structure for many real-world scenarios.
- Efficient searching: Graphs can be searched efficiently using algorithms like depth-first search and breadth-first search.
- Flexibility: Graphs can be easily modified by adding or removing vertices and edges, making them a flexible data structure.
- Supports weighted edges: Graphs can support weighted edges, which is useful when representing relationships with different levels of importance or cost.
- Can represent directed and undirected relationships: Graphs can represent both directed and undirected relationships, making it a versatile data structure.
- Model real-world relationships and connections
- Allow for efficient searching and navigation through the network
- Can handle large and complex datasets
Disadvantages:
- Space complexity: Storing the information about vertices and edges in a graph can be memory-intensive.
- More complex algorithms: The algorithms used to traverse a graph and search for specific vertices or edges can be more complex than other data structures like arrays or linked lists.
- Slower operations: Operations like adding or removing vertices or edges can be slower than with other data structures.
- Difficult to implement: Implementing a graph data structure can be more difficult than other data structures, requiring a good understanding of graph theory and algorithms.
- May not be suitable for some use cases: For certain use cases, a graph data structure may not be the best option and another data structure like an array or linked list may be more suitable.
- May require significant computational resources
- Finding the optimal path between nodes can be a challenging problem
Tries:
Advantages:
- Fast search and retrieval of strings
- Space-efficient storage of strings
- Can be used for text processing tasks such as spell-checking
Disadvantages:
- Can have a high memory overhead for large datasets
- Insertions and deletions can be slow and complex
Segment Trees:
Advantages:
- Efficient range queries and updates
- Can handle large and complex datasets
- Can be used for a variety of range-based problems
Disadvantages:
- Can require significant memory overhead
- The creation of the tree can be a time-consuming process
Suffix Trees:
Advantages:
- Fast string search and pattern matching
- Can handle large and complex datasets
- Can be used for a variety of string-based problems
Disadvantages:
- Can have a high memory overhead
- The creation of the tree can be a time-consuming process
- Not suitable for all string-based problems, such as regular expression matching.
Share your thoughts in the comments
Please Login to comment...