numpy.square() in Python

numpy.square(arr, out = None, ufunc ‘square’) : This mathematical function helps user to calculate square value of each element in the array. Parameters : 

arr  : [array_like] Input array or object
          whose elements, we need to square.

Return : 

An array with square value of each array.  

Code #1 : Working

Python3

# Python program explaining
# square () function

import numpy as np

arr1 = [1, -3, 15, -466]
print ("Square Value of arr1 : \n", np.square(arr1))

arr2 = [23 ,-56]
print ("\nSquare Value of arr2 : ", np.square(arr2))

Output : 

Square Value of arr1 : 
 [     1      9    225 217156]

Square Value of arr2 :  [ 529 3136]

Code #2 : Working with complex numbers

Python3

# Python program explaining
# square () function

import numpy as np

a = 4 + 3j
print("Square(4 + 3j) : ", np.square(a))

b = 16 + 13j
print("\nSquare value(16 + 13j) : ", np.square(b))

Output : 

Square(4 + 3j) :  (7+24j)

Square value(16 + 13j) :  (87+416j)

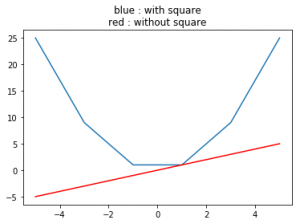
Code #3 : Graphical Representation of numpy.square()

Python3

# Python program explaining
# square () function

import numpy as np
import matplotlib.pyplot as plt

a = np.linspace(start = -5, stop = 5,
                num = 6, endpoint = True)

print("Graphical Representation : \n", np.square(a))

plt.title("blue : with square\nred : without square")
plt.plot(a, np.square(a))

plt.plot(a, a, color = 'red')
plt.show()

Output : 

Graphical Representation : 
 [ 25.   9.   1.   1.   9.  25.]

References : https://docs.scipy.org/doc/numpy-1.13.0/reference/generated/numpy.absolute.html .

using for loop:

In this example, we define a list of numbers called numbers. We then use a for loop to iterate over each number in the list, and calculate the square of each number using the exponentiation operator **. We store each square in a new list called squares. Finally, we print the list of squares to the console.

Note that this approach is not as efficient or concise as using the numpy.square() function, especially if you are working with large arrays of numbers. However, it can be useful if you need to implement your own custom square function or want to understand how the numpy.square() function works internally.

Python3

# Define a list of numbers
numbers = [1, 2, 3, 4, 5]

# Calculate the square of each number using a for loop
squares = []
for number in numbers:
    square = number ** 2
    squares.append(square)

# Print the squares of the numbers
print("The squares of the numbers are:", squares)

Output

The squares of the numbers are: [1, 4, 9, 16, 25]

Approach:
The code defines a list of integers numbers. It then calculates the square of each number in numbers using a for loop, and stores the results in a new list called squares. Finally, the squares of the numbers are printed.

Time Complexity:
The time complexity of the list comprehension is also O(n), where n is the length of the input list numbers. Therefore, the time complexity of both the original code and the alternative code is O(n).

Space Complexity:
The space complexity of the original code and the alternative code is also O(n), because they both create a new list squares to store the results of the square operation, which has the same length as numbers. Additionally, they both use some auxiliary space to store the loop variable and the temporary result of each square operation.