Number of siblings of a given Node in n-ary Tree
Last Updated :
14 Mar, 2023
Given an N-ary tree, find the number of siblings of given node x. Assume that x exists in the given n-ary tree.
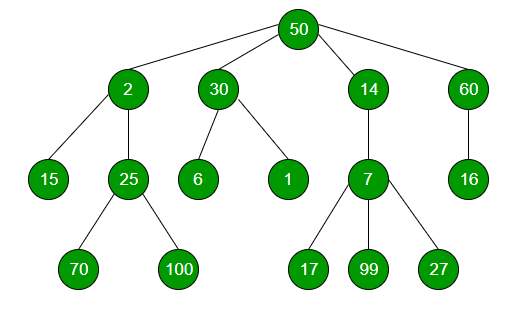
Example :
Input : 30
Output : 3
Approach: For every node in the given n-ary tree, push the children of the current node in the queue. While adding the children of current node in queue, check if any children is equal to the given value x or not. If yes, then return the number of siblings of x.
Below is the implementation of the above idea :
C++
#include <bits/stdc++.h>
using namespace std;
class Node {
public:
int key;
vector<Node*> child;
Node(int data)
{
key = data;
}
};
int numberOfSiblings(Node* root, int x)
{
if (root == NULL)
return 0;
queue<Node*> q;
q.push(root);
while (!q.empty()) {
Node* p = q.front();
q.pop();
for (int i = 0; i < p->child.size(); i++) {
if (p->child[i]->key == x)
return p->child.size() - 1;
q.push(p->child[i]);
}
}
}
int main()
{
Node* root = new Node(50);
(root->child).push_back(new Node(2));
(root->child).push_back(new Node(30));
(root->child).push_back(new Node(14));
(root->child).push_back(new Node(60));
(root->child[0]->child).push_back(new Node(15));
(root->child[0]->child).push_back(new Node(25));
(root->child[0]->child[1]->child).push_back(new Node(70));
(root->child[0]->child[1]->child).push_back(new Node(100));
(root->child[1]->child).push_back(new Node(6));
(root->child[1]->child).push_back(new Node(1));
(root->child[2]->child).push_back(new Node(7));
(root->child[2]->child[0]->child).push_back(new Node(17));
(root->child[2]->child[0]->child).push_back(new Node(99));
(root->child[2]->child[0]->child).push_back(new Node(27));
(root->child[3]->child).push_back(new Node(16));
int x = 100;
cout << numberOfSiblings(root, x) << endl;
return 0;
}
|
Java
import java.util.*;
public class GFG
{
static class Node
{
int key;
Vector<Node> child;
Node(int data)
{
key = data;
child = new Vector<Node>();
}
};
static int numberOfSiblings(Node root, int x)
{
if (root == null)
return 0;
Queue<Node> q = new LinkedList<>();
q.add(root);
while (q.size() > 0)
{
Node p = q.peek();
q.remove();
for (int i = 0; i < p.child.size(); i++)
{
if (p.child.get(i).key == x)
return p.child.size() - 1;
q.add(p.child.get(i));
}
}
return -1;
}
public static void main(String args[])
{
Node root = new Node(50);
(root.child).add(new Node(2));
(root.child).add(new Node(30));
(root.child).add(new Node(14));
(root.child).add(new Node(60));
(root.child.get(0).child).add(new Node(15));
(root.child.get(0).child).add(new Node(25));
(root.child.get(0).child.get(1).child).add(new Node(70));
(root.child.get(0).child.get(1).child).add(new Node(100));
(root.child.get(1).child).add(new Node(6));
(root.child.get(1).child).add(new Node(1));
(root.child.get(2).child).add(new Node(7));
(root.child.get(2).child.get(0).child).add(new Node(17));
(root.child.get(2).child.get(0).child).add(new Node(99));
(root.child.get(2).child.get(0).child).add(new Node(27));
(root.child.get(3).child).add(new Node(16));
int x = 100;
System.out.println( numberOfSiblings(root, x) );
}
}
|
Python3
from queue import Queue
class newNode:
def __init__(self,data):
self.child = []
self.key = data
def numberOfSiblings(root, x):
if (root == None):
return 0
q = Queue()
q.put(root)
while (not q.empty()):
p = q.queue[0]
q.get()
for i in range(len(p.child)):
if (p.child[i].key == x):
return len(p.child) - 1
q.put(p.child[i])
if __name__ == '__main__':
root = newNode(50)
(root.child).append(newNode(2))
(root.child).append(newNode(30))
(root.child).append(newNode(14))
(root.child).append(newNode(60))
(root.child[0].child).append(newNode(15))
(root.child[0].child).append(newNode(25))
(root.child[0].child[1].child).append(newNode(70))
(root.child[0].child[1].child).append(newNode(100))
(root.child[1].child).append(newNode(6))
(root.child[1].child).append(newNode(1))
(root.child[2].child).append(newNode(7))
(root.child[2].child[0].child).append(newNode(17))
(root.child[2].child[0].child).append(newNode(99))
(root.child[2].child[0].child).append(newNode(27))
(root.child[3].child).append(newNode(16))
x = 100
print(numberOfSiblings(root, x))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
public class Node
{
public int key;
public List<Node> child;
public Node(int data)
{
key = data;
child = new List<Node>();
}
};
static int numberOfSiblings(Node root, int x)
{
if (root == null)
return 0;
Queue<Node> q = new Queue<Node>();
q.Enqueue(root);
while (q.Count > 0)
{
Node p = q.Peek();
q.Dequeue();
for (int i = 0; i < p.child.Count; i++)
{
if (p.child[i].key == x)
return p.child.Count - 1;
q.Enqueue(p.child[i]);
}
}
return -1;
}
public static void Main(String []args)
{
Node root = new Node(50);
(root.child).Add(new Node(2));
(root.child).Add(new Node(30));
(root.child).Add(new Node(14));
(root.child).Add(new Node(60));
(root.child[0].child).Add(new Node(15));
(root.child[0].child).Add(new Node(25));
(root.child[0].child[1].child).Add(new Node(70));
(root.child[0].child[1].child).Add(new Node(100));
(root.child[1].child).Add(new Node(6));
(root.child[1].child).Add(new Node(1));
(root.child[2].child).Add(new Node(7));
(root.child[2].child[0].child).Add(new Node(17));
(root.child[2].child[0].child).Add(new Node(99));
(root.child[2].child[0].child).Add(new Node(27));
(root.child[3].child).Add(new Node(16));
int x = 100;
Console.WriteLine( numberOfSiblings(root, x));
}
}
|
Javascript
<script>
class Node
{
constructor(data)
{
this.key = data;
this.child = [];
}
};
function numberOfSiblings(root, x)
{
if (root == null)
return 0;
var q = [];
q.push(root);
while (q.length > 0)
{
var p = q[0];
q.shift();
for (var i = 0; i < p.child.length; i++)
{
if (p.child[i].key == x)
return p.child.length - 1;
q.push(p.child[i]);
}
}
return -1;
}
var root = new Node(50);
(root.child).push(new Node(2));
(root.child).push(new Node(30));
(root.child).push(new Node(14));
(root.child).push(new Node(60));
(root.child[0].child).push(new Node(15));
(root.child[0].child).push(new Node(25));
(root.child[0].child[1].child).push(new Node(70));
(root.child[0].child[1].child).push(new Node(100));
(root.child[1].child).push(new Node(6));
(root.child[1].child).push(new Node(1));
(root.child[2].child).push(new Node(7));
(root.child[2].child[0].child).push(new Node(17));
(root.child[2].child[0].child).push(new Node(99));
(root.child[2].child[0].child).push(new Node(27));
(root.child[3].child).push(new Node(16));
var x = 100;
document.write( numberOfSiblings(root, x));
</script>
|
Complexity Analysis:
- Time Complexity: O(N), where N is the number of nodes in tree.
- Auxiliary Space: O(N), where N is the number of nodes in tree.
Example no 2:
Algorithmic steps for implementing the given concept:
Create a hash map to store the parent of each node.
For each node in the tree, map it to its parent in the hash map.
Given the node for which you want to find the number of siblings, look up its parent in the hash map.
If the parent is not found, return 0 as the node has no siblings.
If the parent is found, count the number of children the parent has.
Return the count minus 1 as the given node is included in the count.
Note: This algorithm assumes that the parent array is complete and accurately represents the n-ary tree.
Program: Implementing the given concept by using hash map:
C++
#include <iostream>
#include <vector>
#include <unordered_map>
using namespace std;
int findSiblingCount(int node, unordered_map<int, vector<int>> &treeMap) {
int parent = treeMap.count(node) ? treeMap[node][0] : -1;
if (parent == -1) {
return 0;
}
int siblingCount = treeMap[parent].size() - 1;
return siblingCount;
}
int main() {
unordered_map<int, vector<int>> treeMap;
treeMap[0] = {-1, 1, 2, 3};
treeMap[1] = {0, 4, 5};
treeMap[2] = {0, 6};
treeMap[3] = {0};
treeMap[4] = {1};
treeMap[5] = {1};
treeMap[6] = {2};
int node = 4;
cout << "The number of siblings for node " << node << " is: " << findSiblingCount(node, treeMap) << endl;
return 0;
}
|
Java
import java.util.ArrayList;
import java.util.HashMap;
import java.util.List;
import java.util.Map;
public class SiblingCounter {
public static int findSiblingCount(int node,Map<Integer, List<Integer> > treeMap)
{
int parent = treeMap.containsKey(node)
? treeMap.get(node).get(0)
: -1;
if (parent == -1) {
return 0;
}
int siblingCount = treeMap.get(parent).size() - 1;
return siblingCount;
}
public static void main(String[] args)
{
Map<Integer, List<Integer> > treeMap = new HashMap<>();
treeMap.put(0, new ArrayList<Integer>() {{add(-1);
add(1);
add(2);
add(3);
}
});
treeMap.put(1, new ArrayList<Integer>() {
{
add(0);
add(4);
add(5);
}
});
treeMap.put(2, new ArrayList<Integer>() {
{
add(0);
add(6);
}
});
treeMap.put(3, new ArrayList<Integer>() {
{
add(0);
}
});
treeMap.put(4, new ArrayList<Integer>() {
{
add(1);
}
});
treeMap.put(5, new ArrayList<Integer>() {
{
add(1);
}
});
treeMap.put(6, new ArrayList<Integer>() {
{
add(2);
}
});
int node = 4;
System.out.println(
"The number of siblings for node " + node
+ " is: " + findSiblingCount(node, treeMap));
}
}
|
Python3
def findSiblingCount(node, treeMap):
parent = treeMap[node][0] if node in treeMap else -1
if parent == -1:
return 0
siblingCount = len(treeMap[parent]) - 1
return siblingCount
treeMap = {
0: [-1, 1, 2, 3],
1: [0, 4, 5],
2: [0, 6],
3: [0],
4: [1],
5: [1],
6: [2]
}
node = 4
print(f"The number of siblings for node {node} is: {findSiblingCount(node, treeMap)}")
|
Javascript
let treeMap = new Map();
treeMap.set(0, [-1, 1, 2, 3]);
treeMap.set(1, [0, 4, 5]);
treeMap.set(2, [0, 6]);
treeMap.set(3, [0]);
treeMap.set(4, [1]);
treeMap.set(5, [1]);
treeMap.set(6, [2]);
function findSiblingCount(node, treeMap) {
let parent = treeMap.has(node) ? treeMap.get(node)[0] : -1;
if (parent === -1) {
return 0;
}
let siblingCount = treeMap.get(parent).length - 1;
return siblingCount;
}
let node = 4;
console.log(`The number of siblings for node ${node} is: ${findSiblingCount(node, treeMap)}`);
|
C#
using System;
using System.Collections.Generic;
class Program
{
static int FindSiblingCount(int node, Dictionary<int, List<int>> treeMap)
{
int parent = treeMap.ContainsKey(node) ? treeMap[node][0] : -1;
if (parent == -1)
{
return 0;
}
int siblingCount = treeMap[parent].Count - 1;
return siblingCount;
}
static void Main(string[] args)
{
Dictionary<int, List<int>> treeMap = new Dictionary<int, List<int>>();
treeMap[0] = new List<int> { -1, 1, 2, 3 };
treeMap[1] = new List<int> { 0, 4, 5 };
treeMap[2] = new List<int> { 0, 6 };
treeMap[3] = new List<int> { 0 };
treeMap[4] = new List<int> { 1 };
treeMap[5] = new List<int> { 1 };
treeMap[6] = new List<int> { 2 };
int node = 4;
Console.WriteLine("The number of siblings for node " + node + " is: " + FindSiblingCount(node, treeMap));
}
}
|
Output
The number of siblings for node 4 is: 2
Explanation:
In this implementation, the findSiblingCount function takes a node and the tree represented as a hash map as inputs and returns the number of siblings the node has. If the node is not found in the tree map, it returns 0 as the node has no siblings. If the node is found, the function looks up the parent of the node in the tree map and returns the number of children the parent has minus 1, which represents the number of siblings the node has.
Time and Space complexities for above program:
The time complexity of the above code is O(1) because the findSiblingCount function takes constant time to find the number of siblings of a given node. This is because the hash map is used to store the parent of each node, so looking up the parent of a given node takes constant time. The same holds true for counting the number of children the parent has.
The space complexity of the above code is O(n), where n is the number of nodes in the n-ary tree. This is because the hash map is used to store the parent of each node and the children of each parent, so the space required is proportional to the number of nodes in the tree.
Note: The space complexity assumes that the hash map is used to represent the tree and the number of children each node has is constant, so the space used is linear in the number of nodes. If the number of children each node has is not constant, the space complexity would be higher.
Share your thoughts in the comments
Please Login to comment...