Number of possible Functions
Last Updated :
25 Nov, 2019
In the below articles, we are going to calculate the number of functions possible from given two sets of the element.
Statement:
Suppose there are two sets ‘A’ and ‘B’ containing ‘n’ and ‘m’ number of elements respectively, i.e., Sets,
'A' = {1, 2, 3, 4, ............, n},
'B' = {1, 2, 3, 4, ............, m}
Then the number of function possible will be
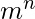
when functions are counted from set ‘A’ to ‘B’ and
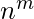
when function are counted from set ‘B’ to ‘A’.
Explanation:
In the below diagram, as we can see that Set ‘A’ contain ‘n’ elements and set ‘B’ contain ‘m’ element. Each element of set ‘A’ makes ‘m’ number of functions with each element of the set ‘B’ and hence total number of functions possible is
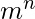
.
 Examples:
Examples:
- If set ‘A’ contain ‘3’ element and set ‘B’ contain ‘2’ elements then total number of function possible will be
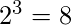 .
.
- If set ‘A’ contain ‘5’ element and set ‘B’ contain ‘2’ elements then total number of function possible will be
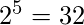 .
.
But when functions are counted from set ‘B’ to ‘A’ then the formula will be
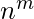
where n, m are the number of elements present in set ‘A’ and ‘B’ respectively then examples will be like below:
- If set ‘A’ contain ‘3’ element and set ‘B’ contain ‘2’ elements then the total number of functions possible will be
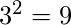 .
.
- If set ‘A’ contain ‘5’ element and set ‘B’ contain ‘2’ elements then the total number of function possible will be
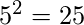 .
.
Similarly when the two sets increases to 3 sets,
'A' = {1, 2, 3, 4, ............, n},
'B' = {1, 2, 3, 4, ............, m}
'C' = {1, 2, 3, 4, ............, p}
Then the number of possible function will be
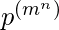
when the function is counted from Set ‘A’ to ‘B’ then to ‘C’ and thus so on for any number of sets.
Share your thoughts in the comments
Please Login to comment...