Minimum size binary string required such that probability of deleting two 1’s at random is 1/X
Last Updated :
10 May, 2021
Given a value X, the task is to find a minimum size binary string, such that if any 2 characters are deleted at random, the probability that both the characters will be ‘1’ is 1/X. Print the size of such binary string.
Example:
Input: X = 2
Output: 4
Explanation:
Let the binary string be “0111”.
Probability of choosing 2 1s from given string is = 3C2 / 4C2 = 3/6 = 1/2 (which is equal to 1/X).
Hence, the required size is 4.
(Any 4 size binary string with 3 ‘1’s and 1 ‘0’ can be taken for this example).
Input: X = 8
Output: 5
Approach: We will try to find a formula to solve this problem.
Let
r = Number of 1’s in the string
and
b = Number of 0’s in the string.
- If two characters are deleted at random, then
Total number of ways = (r + b) C 2.
- If 2 characters are desired to be 1’s, Favourable number of cases = r C 2.
- Hence, P(both are 1’s) = rC2 / (r + b)C2.
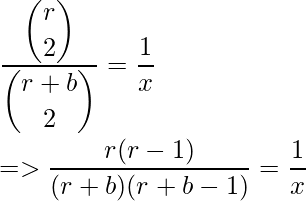
- A tricky observation to further proceed our calculation is:
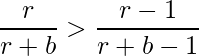
- Squaring the inequality and comparing with the equality, we get
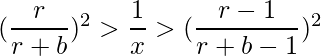
- If r > 1, we take square root on all 3 sides.
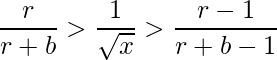
- Taking the leftmost part of the inequality, we get:
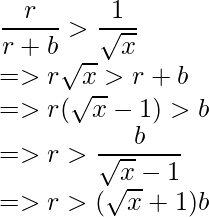
- Similarly, taking the rightmost part of the inequality, we get:
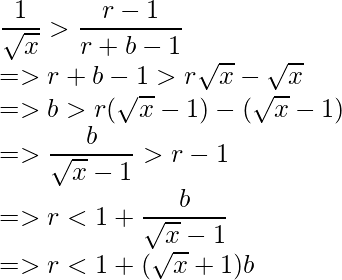
- Combining the derived conclusions, we get the range of r in terms of b.
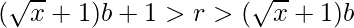
- For the minimum value of string, we set b = 1
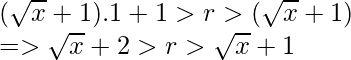
- In order to get a valid minimum r, we take the first integer value of r in this range.
For Example: if X = 2
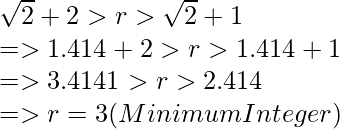
Hence, r = 3 and b = 1.
P(both character are 1’s) = 3C2 / 4C2 = 2/4 = 1/2
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
int MinimumString(int x)
{
int b = 1;
double left_lim = sqrt(x) + 1.0;
double right_lim = sqrt(x) + 2.0;
int r;
for (int i = left_lim; i <= right_lim; i++) {
if (i > left_lim and i < right_lim) {
r = i;
break;
}
}
return b + r;
}
int main()
{
int X = 2;
cout << MinimumString(X);
return 0;
}
|
Java
import java.util.*;
class GFG{
static int MinimumString(int x)
{
int b = 1;
double left_lim = Math.sqrt(x) + 1.0;
double right_lim = Math.sqrt(x) + 2.0;
int r = 0;
for(int i = (int)left_lim; i <= right_lim; i++)
{
if (i > left_lim && i < right_lim)
{
r = i;
break;
}
}
return b + r;
}
public static void main(String[] args)
{
int X = 2;
System.out.print(MinimumString(X));
}
}
|
Python3
from math import sqrt
def MinimumString(x):
b = 1
left_lim = sqrt(x) + 1.0
right_lim = sqrt(x) + 2.0
for i in range(int(left_lim),
int(right_lim) + 1):
if(i > left_lim and i < right_lim):
r = i
break
return b + r
if __name__ == '__main__':
X = 2
print(MinimumString(X))
|
C#
using System;
class GFG{
static int MinimumString(int x)
{
int b = 1;
double left_lim = Math.Sqrt(x) + 1.0;
double right_lim = Math.Sqrt(x) + 2.0;
int r = 0;
for(int i = (int)left_lim; i <= right_lim; i++)
{
if (i > left_lim && i < right_lim)
{
r = i;
break;
}
}
return b + r;
}
public static void Main(String[] args)
{
int X = 2;
Console.Write(MinimumString(X));
}
}
|
Javascript
<script>
function MinimumString(x)
{
let b = 1;
let left_lim = Math.sqrt(x) + 1.0;
let right_lim = Math.sqrt(x) + 2.0;
let r = 0;
for(let i = Math.floor(left_lim); i <= Math.floor(right_lim); i++)
{
if (i > left_lim && i < right_lim)
{
r = i;
break;
}
}
return b + r;
}
let X = 2;
document.write(MinimumString(X));
</script>
|
Time Complexity: O(1), as the difference between left_lim and right_lim will be always less than 1.
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...