Minimum number of pigs required to find the poisonous bucket
Last Updated :
15 Dec, 2023
Given an integer N denoting the number of buckets, and an integer M, denoting the minimum time in minutes required by a pig to die after drinking poison, the task is to find the minimum number of pigs required to figure out which bucket is poisonous within P minutes, if there is exactly one bucket with poison, while the rest is filled with water.
Examples:
Input: N = 1000, M = 15, P = 60
Output: 5
Explanation: Minimum number of pigs required to find the poisonous bucket is 5.
Input: N = 4, M = 15, P = 15
Output: 2
Explanation: Minimum number of pigs required to find the poisonous bucket is 2.
Approach: The given problem can be solved using the given observations:
- A pig can be allowed to drink simultaneously on as many buckets as one would like, and the feeding takes no time.
- After a pig has instantly finished drinking buckets, there has to be a cool downtime of M minutes. During this time, only observation is allowed and no feedings at all.
- Any given bucket can be sampled an infinite number of times (by an unlimited number of pigs).
Now, P minutes to test and M minutes to die simply tells how many rounds the pigs can be used, i.e., how many times a pig can eat. Therefore, declare a variable called r = P(Minutes To Test) / M(Minutes To Die).
Consider the cases to understand the approach:
Case 1: If r = 1, i.e., the number of rounds is 1.
Example: 4 buckets, 15 minutes to die, and 15 minutes to test. The answer is 2. Suppose A and B represent 2 pigs, then the cases are:

Obviously, using the binary form to represent the solution as:
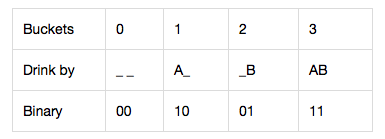
Conclusion: If there are x pigs, they can represent (encode) 2x buckets.
Case 2: If r > 1, i.e. the number of rounds is more than 1. Let below be the following notations:
- 0 means the pig does not drink and die.
- 1 means the pig drinks in the first (and only) round.
Generalizing the above results(t means the pig drinks in the t round and die): If there are t attempts, a (t + 1)-based number is used to represent (encode) the buckets. (That’s also why the first conclusion uses the 2-based number)
Example: 8 buckets, 15 minutes to die, and 40 minutes to test. Now, there are 2 (= (40/15).floor) attempts, as a result, 3-based number is used to encode the buckets. The minimum number of pigs required are 2 (= Math.log(8, 3).ceil).

Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void poorPigs(int buckets,
int minutesToDie,
int minutesToTest)
{
cout << ceil(log(buckets)
/ log((minutesToTest
/ minutesToDie)
+ 1));
}
int main()
{
int N = 1000, M = 15, P = 60;
poorPigs(N, M, P);
return 0;
}
|
Java
import java.io.*;
class GFG
{
static void poorPigs(int buckets, int minutesToDie,
int minutesToTest)
{
System.out.print((int)Math.ceil(
Math.log(buckets)
/ Math.log((minutesToTest / minutesToDie)
+ 1)));
}
public static void main(String[] args)
{
int N = 1000, M = 15, P = 60;
poorPigs(N, M, P);
}
}
|
Python3
import math
def poorPigs(buckets, minutesToDie, minutesToTest):
print(math.ceil(math.log(buckets)\
// math.log((minutesToTest \
// minutesToDie) + 1)));
if __name__ == '__main__':
N = 1000;
M = 15;
P = 60;
poorPigs(N, M, P);
|
C#
using System;
class GFG
{
static void poorPigs(int buckets, int minutesToDie,
int minutesToTest)
{
Console.WriteLine((int)Math.Ceiling(
Math.Log(buckets)
/ Math.Log((minutesToTest / minutesToDie)
+ 1)));
}
static public void Main()
{
int N = 1000, M = 15, P = 60;
poorPigs(N, M, P);
}
}
|
Javascript
<script>
function poorPigs(buckets, minutesToDie,
minutesToTest)
{
document.write(Math.ceil(
Math.log(buckets)
/ Math.log((minutesToTest / minutesToDie)
+ 1)));
}
let N = 1000, M = 15, P = 60;
poorPigs(N, M, P);
</script>
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...