Minimum number of given operations required to convert a permutation into an identity permutation
Last Updated :
09 Mar, 2023
Given a permutation P (P1, P2, P3, … Pn) of first n natural numbers. Find the minimum number of operations to convert it into an identity permutation i.e. 1, 2, 3, …, n where each operation is defined as:
P[i] = P[P[P[i]]] 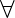 i from 1 to n (1 based indexing). If there is no way to convert then print -1.
i from 1 to n (1 based indexing). If there is no way to convert then print -1.
Examples:
Input: arr[] = {2, 3, 1}
Output: 1
After 1 operation:
P[1] = P[P[P[1]]] = P[P[2]] = P[3] = 1
P[2] = P[P[P[2]]] = P[P[3]] = P[1] = 2
P[3] = P[P[P[3]]] = P[P[1]] = P[2] = 3
Thus after 1 operation we obtain an identity permutation.
Input: arr[] = {2, 1, 3}
Output: -1
There is no way to obtain identity permutation
no matter how many operations we apply.
Approach: First, find all the cycles in the given permutation. Here, a cycle is a directed graph in which there is an edge from an element e to the element on position e.
For example, Here’s the graph for permutation {4, 6, 5, 3, 2, 1, 8, 7}
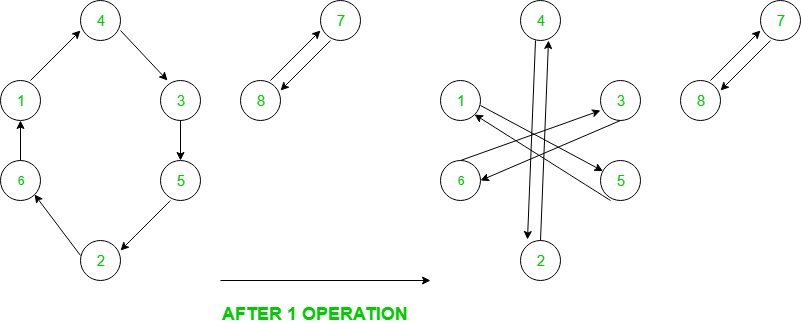
Now in one operation, each cycle of length 3k breaks into 3 cycles each of length k while cycles of length 3k+1 or 3k+2 do not break. Since in the end, we need all cycles of length 1, therefore, all cycles must be a power of 3 otherwise answer doesn’t exist. The answer would then be the maximum of log(base 3) of all cycle lengths.
Algorithm:
Step 1: Create the calculateCycleOperations function, which accepts an integer as an input named “len”.
Step 2: Initialize the cycle operations variable with a value of 0 within the function. Step 3: Start a while loop with the condition “len” is positive.
a. divided “len” by three and update it every time
b. divided “len” by three and update it every time Step 4: Return the cycle operations value that has been reduced by 1.
Step 5: Create the function minimumOperations, which has two inputs: an integer array p[] and an integer n.
Step 6: Set all values in a boolean array with the name visited and a size of n+1 to 0.
Step 7: create the variable “ans” with the value 0.
Step 8: start a for loop and traverse through each element of the array.
a. If the current element is not present in previous cycles, then only consider it.
b. Mark the current element as visited so that it will not be considered in other cycles.
c. Initialize a variable named ele as the current element, and a variable named len as 1.
d. Start a while loop with the condition element is not visited
1. Update the value of ele with p[ele], and increment len by 1
e. Calculate the number of operations needed for this cycle to reduce to length 1 (if possible) by calling the function calculateCycleOperations.
f. Check if the length of the cycle is a power of 3, if not, then return -1.
g. Take the maximum of the operations and ans.
Step 8: Return ans
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int calculateCycleOperations(int len)
{
int cycle_operations = 0;
while (len) {
len /= 3;
++cycle_operations;
}
return --cycle_operations;
}
int minimumOperations(int p[], int n)
{
bool visited[n + 1] = { 0 };
int ans = 0;
for (int i = 1; i <= n; i++) {
int ele = p[i];
if (!visited[ele]) {
visited[ele] = 1;
int len = 1;
ele = p[ele];
while (!visited[ele]) {
visited[ele] = 1;
++len;
ele = p[ele];
}
int operations = calculateCycleOperations(len);
int num = pow(3, operations);
if (num != len) {
return -1;
}
ans = max(ans, operations);
}
}
return ans;
}
int main()
{
int P[] = { -1, 4, 6, 5, 3, 2, 7, 8, 9, 1 };
int n = (sizeof(P) / sizeof(P[0])) - 1;
cout << minimumOperations(P, n);
return 0;
}
|
Java
import java.util.*;
class GFG {
static int calculateCycleOperations(int len)
{
int cycle_operations = 0;
while (len > 0) {
len /= 3;
++cycle_operations;
}
return --cycle_operations;
}
static int minimumOperations(int p[], int n)
{
int[] visited = new int[n + 1];
Arrays.fill(visited, 0);
int ans = 0;
for (int i = 1; i <= n; i++) {
int ele = p[i];
if (visited[ele] == 0) {
visited[ele] = 1;
int len = 1;
ele = p[ele];
while (visited[ele] == 0) {
visited[ele] = 1;
++len;
ele = p[ele];
}
int operations
= calculateCycleOperations(len);
int num = (int)Math.pow(3, operations);
if (num != len) {
return -1;
}
ans = Math.max(ans, operations);
}
}
return ans;
}
public static void main(String args[])
{
int P[] = { -1, 4, 6, 5, 3, 2, 7, 8, 9, 1 };
int n = P.length - 1;
System.out.println(minimumOperations(P, n));
}
}
|
Python3
def calculateCycleOperations(length):
cycle_operations = 0
while length > 0:
length //= 3
cycle_operations += 1
return cycle_operations - 1
def minimumOperations(p, n):
visited = [0] * (n + 1)
ans = 0
for i in range(1, n + 1):
ele = p[i]
if not visited[ele]:
visited[ele] = 1
length = 1
ele = p[ele]
while not visited[ele]:
visited[ele] = 1
length += 1
ele = p[ele]
operations = calculateCycleOperations(length)
num = pow(3, operations)
if num != length:
return -1
ans = max(ans, operations)
return ans
if __name__ == "__main__":
P = [-1, 4, 6, 5, 3, 2, 7, 8, 9, 1]
n = len(P) - 1
print(minimumOperations(P, n))
|
C#
using System;
class GFG {
static int calculateCycleOperations(int len)
{
int cycle_operations = 0;
while (len > 0) {
len /= 3;
++cycle_operations;
}
return --cycle_operations;
}
static int minimumOperations(int[] p, int n)
{
int[] visited = new int[n + 1];
int ans = 0;
for (int i = 1; i <= n; i++) {
int ele = p[i];
if (visited[ele] == 0) {
visited[ele] = 1;
int len = 1;
ele = p[ele];
while (visited[ele] == 0) {
visited[ele] = 1;
++len;
ele = p[ele];
}
int operations
= calculateCycleOperations(len);
int num = (int)Math.Pow(3, operations);
if (num != len) {
return -1;
}
ans = Math.Max(ans, operations);
}
}
return ans;
}
public static void Main()
{
int[] P = { -1, 4, 6, 5, 3, 2, 7, 8, 9, 1 };
int n = P.Length - 1;
Console.WriteLine(minimumOperations(P, n));
}
}
|
PHP
<?php
function calculateCycleOperations($len)
{
$cycle_operations = 0;
while ($len)
{
$len = (int)($len / 3);
++$cycle_operations;
}
return --$cycle_operations;
}
function minimumOperations($p, $n)
{
$visited[$n + 1] = array(0);
$ans = 0;
for ($i = 1; $i <= $n; $i++)
{
$ele = $p[$i];
if (!$visited[$ele])
{
$visited[$ele] = 1;
$len = 1;
$ele = $p[$ele];
while (!$visited[$ele])
{
$visited[$ele] = 1;
++$len;
$ele = $p[$ele];
}
$operations = calculateCycleOperations($len);
$num = pow(3, $operations);
if ($num != $len)
{
return -1;
}
$ans = max($ans, $operations);
}
}
return $ans;
}
$P = array(-1, 4, 6, 5, 3, 2, 7, 8, 9, 1);
$n = sizeof($P) - 1;
echo minimumOperations($P, $n);
?>
|
Javascript
<script>
function calculateCycleOperations(len)
{
let cycle_operations = 0;
while (len > 0)
{
len = Math.floor(len / 3);
++cycle_operations;
}
return --cycle_operations;
}
function minimumOperations(p, n)
{
let visited = Array.from({length: n + 1}, (_, i) => 0);
let ans = 0;
for (let i = 1; i <= n; i++)
{
let ele = p[i];
if (visited[ele] == 0)
{
visited[ele] = 1;
let len = 1;
ele = p[ele];
while (visited[ele] == 0)
{
visited[ele] = 1;
++len;
ele = p[ele];
}
let operations = calculateCycleOperations(len);
let num = Math.floor(Math.pow(3, operations));
if (num != len) {
return -1;
}
ans = Math.max(ans, operations);
}
}
return ans;
}
let P = [ -1, 4, 6, 5, 3, 2, 7, 8, 9, 1 ];
let n = P.length - 1;
document.write(minimumOperations(P, n));
</script>
|
Time Complexity: O(N*LogN)
Auxiliary Space: O(N)
Share your thoughts in the comments
Please Login to comment...