Maximum XOR of Two Numbers in an Array

Given an array Arr of non-negative integers of size N. The task is to find the maximum possible xor between two numbers present in the array.
Example: 

Input: Arr = {25, 10, 2, 8, 5, 3} 
Output: 28 
Explanation: The maximum result is 5 ^ 25 = 28 

Input: Arr = {1, 2, 3, 4, 5, 6, 7} 
Output: 7 
Explanation: The maximum result is 1 ^ 6 = 7 

Naive Approach: A Simple Solution is to generate all pairs of the given array and compute the XOR of the pairs. Finally, return the maximum XOR value. This solution takes 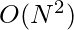time.
Below is the implementation of the above approach: 

C++

// C++ implementation
#include <bits/stdc++.h>
using namespace std;

// Function to return the
// maximum xor
int max_xor(int arr[], int n)
{

    int maxXor = 0;

    // Calculating xor of each pair
    for (int i = 0; i < n; i++) {
        for (int j = i + 1; j < n; j++) {
            maxXor = max(maxXor,
                         arr[i] ^ arr[j]);
        }
    }
    return maxXor;
}

// Driver Code
int main()
{

    int arr[] = { 25, 10, 2, 8, 5, 3 };
    int n = sizeof(arr) / sizeof(arr[0]);

    cout << max_xor(arr, n) << endl;
    return 0;
}

Java

// Java implementation of the approach
class GFG
{

    // Function to return the
    // maximum xor
    static int max_xor(int arr[], int n)
    {
        int maxXor = 0;

        // Calculating xor of each pair
        for (int i = 0; i < n; i++)
        {
            for (int j = i + 1; j < n; j++)
            {
                maxXor = Math.max(maxXor,
                        arr[i] ^ arr[j]);
            }
        }
        return maxXor;
    }

    // Driver Code
    public static void main(String[] args)
    {
        int arr[] = {25, 10, 2, 8, 5, 3};
        int n = arr.length;

        System.out.println(max_xor(arr, n));
    }
}

// This code is contributed by Rajput-Ji

Python3

# Python3 implementation

# Function to return the
# maximum xor
def max_xor(arr, n):

    maxXor = 0;

    # Calculating xor of each pair
    for i in range(n):
        for j in range(i + 1, n):
            maxXor = max(maxXor,\
                         arr[i] ^ arr[j]);

    return maxXor;

# Driver Code
if __name__ == '__main__':

    arr = [ 25, 10, 2, 8, 5, 3 ];
    n = len(arr);

    print(max_xor(arr, n));

# This code is contributed by 29AjayKumar

C#

// C# implementation of the approach
using System;

class GFG
{

// Function to return the
// maximum xor
static int max_xor(int []arr, int n)
{
    int maxXor = 0;

    // Calculating xor of each pair
    for (int i = 0; i < n; i++)
    {
        for (int j = i + 1; j < n; j++)
        {
            maxXor = Math.Max(maxXor,
                              arr[i] ^ arr[j]);
        }
    }
    return maxXor;
}

// Driver Code
public static void Main()
{
    int []arr = {25, 10, 2, 8, 5, 3};
    int n = arr.Length;

    Console.WriteLine(max_xor(arr, n));
}
}

// This code is contributed by AnkitRai01

Javascript

<script>

// Javascript implementation

// Function to return the
// maximum xor
function max_xor(arr, n)
{

    let maxXor = 0;

    // Calculating xor of each pair
    for (let i = 0; i < n; i++) {
        for (let j = i + 1; j < n; j++) {
            maxXor = Math.max(maxXor,
                         arr[i] ^ arr[j]);
        }
    }
    return maxXor;
}

// Driver Code

    let arr = [ 25, 10, 2, 8, 5, 3 ];
    let n = arr.length;

    document.write(max_xor(arr, n));

</script>

Output

28

Time Complexity: O(N^{2})           , where N is the size of the array
Auxiliary Space: O(1)
Efficient Approach: The approach is similar to this article where the task is to find the maximum AND value pair. 
So the idea is to change the problem statement from finding the maximum xor of two numbers in an array to -> find two numbers in an array, such that xor of which equals to a number X. In this case, X will be the maximum number we want to achieve till i-th bit.
To find the largest value of an XOR operation, the value of xor should have every bit to be a set bit i.e 1. In a 32-bit number, the goal is to get the most 1 set starting left to right.
To evaluate each bit, there is a mask needed for that bit. A mask defines which bit should be present in the answer and which bit is not. Here we will use a mask to keep the prefix for every number ( means by taking the ans with the mask how many bits are remaining from the number ) in the input till the i-th bit then with the list of possible numbers in our set, after inserting the number we will evaluate if we can update the max for that bit position to be 1.
Below is the implementation of the above approach: 

C++

// C++ implementation of the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to return the
// maximum xor
int max_xor(int arr[], int n)
{
    int maxx = 0, mask = 0;

    set<int> se;

    for (int i = 30; i >= 0; i--) {

        // set the i'th bit in mask
        // like 100000, 110000, 111000..
        mask |= (1 << i);

        for (int i = 0; i < n; ++i) {

            // Just keep the prefix till
            // i'th bit neglecting all
            // the bit's after i'th bit
            se.insert(arr[i] & mask);
        }

        int newMaxx = maxx | (1 << i);

        for (int prefix : se) {

            // find two pair in set
            // such that a^b = newMaxx
            // which is the highest
            // possible bit can be obtained
            if (se.count(newMaxx ^ prefix)) {
                maxx = newMaxx;
                break;
            }
        }

        // clear the set for next
        // iteration
        se.clear();
    }

    return maxx;
}

// Driver Code
int main()
{

    int arr[] = { 25, 10, 2, 8, 5, 3 };
    int n = sizeof(arr) / sizeof(arr[0]);

    cout << max_xor(arr, n) << endl;

    return 0;
}

Java

// Java implementation of the above approach
import java.util.*;
class GFG
{

// Function to return the
// maximum xor
static int max_xor(int arr[], int n)
{
    int maxx = 0, mask = 0;

    HashSet<Integer> se = new HashSet<Integer>();

    for (int i = 30; i >= 0; i--)
    {

        // set the i'th bit in mask
        // like 100000, 110000, 111000..
        mask |= (1 << i);

        for (int j = 0; j < n; ++j)
        {

            // Just keep the prefix till
            // i'th bit neglecting all
            // the bit's after i'th bit
            se.add(arr[j] & mask);
        }

        int newMaxx = maxx | (1 << i);

        for (int prefix : se)
        {

            // find two pair in set
            // such that a^b = newMaxx
            // which is the highest
            // possible bit can be obtained
            if (se.contains(newMaxx ^ prefix))
            {
                maxx = newMaxx;
                break;
            }
        }

        // clear the set for next
        // iteration
        se.clear();
    }
    return maxx;
}

// Driver Code
public static void main(String[] args)
{
    int arr[] = { 25, 10, 2, 8, 5, 3 };
    int n = arr.length;

    System.out.println(max_xor(arr, n));
}
}

// This code is contributed by Rajput-Ji

Python3

# Python3 implementation of the above approach

# Function to return the
# maximum xor
def max_xor( arr , n):

    maxx = 0
    mask = 0;

    se = set()

    for i in range(30, -1, -1):

        # set the i'th bit in mask
        # like 100000, 110000, 111000..
        mask |= (1 << i)
        newMaxx = maxx | (1 << i)

        for i in range(n):

            # Just keep the prefix till
            # i'th bit neglecting all
            # the bit's after i'th bit
            se.add(arr[i] & mask)

        for prefix in se:

            # find two pair in set
            # such that a^b = newMaxx
            # which is the highest
            # possible bit can be obtained
            if (newMaxx ^ prefix) in se:
                maxx = newMaxx
                break

        # clear the set for next
        # iteration
        se.clear()
    return maxx

# Driver Code
arr = [ 25, 10, 2, 8, 5, 3 ]
n = len(arr)
print(max_xor(arr, n))

# This code is contributed by ANKITKUMAR34

C#

// C# implementation of the above approach
using System;
using System.Collections.Generic;

class GFG
{

// Function to return the
// maximum xor
static int max_xor(int []arr, int n)
{
    int maxx = 0, mask = 0;

    HashSet<int> se = new HashSet<int>();

    for (int i = 30; i >= 0; i--)
    {

        // set the i'th bit in mask
        // like 100000, 110000, 111000..
        mask |= (1 << i);

        for (int j = 0; j < n; ++j)
        {

            // Just keep the prefix till
            // i'th bit neglecting all
            // the bit's after i'th bit
            se.Add(arr[j] & mask);
        }

        int newMaxx = maxx | (1 << i);

        foreach (int prefix in se)
        {

            // find two pair in set
            // such that a^b = newMaxx
            // which is the highest
            // possible bit can be obtained
            if (se.Contains(newMaxx ^ prefix))
            {
                maxx = newMaxx;
                break;
            }
        }

        // clear the set for next
        // iteration
        se.Clear();
    }
    return maxx;
}

// Driver Code
public static void Main(String[] args)
{
    int []arr = { 25, 10, 2, 8, 5, 3 };
    int n = arr.Length;

    Console.WriteLine(max_xor(arr, n));
}
}

// This code is contributed by Princi Singh

Javascript

<script>

// Javascript implementation of the above approach

// Function to return the
// maximum xor
function max_xor(arr, n)
{
    let maxx = 0, mask = 0;

    var se = new Set();

    for (let i = 30; i >= 0; i--)
    {

        // set the i'th bit in mask
        // like 100000, 110000, 111000..
        mask |= (1 << i);

        for (let j = 0; j < n; ++j)
        {

            // Just keep the prefix till
            // i'th bit neglecting all
            // the bit's after i'th bit
            se.add(arr[j] & mask);
        }

        let newMaxx = maxx | (1 << i);

        //for (let prefix in se)
        for (let prefix of se.keys())
        {

            // find two pair in set
            // such that a^b = newMaxx
            // which is the highest
            // possible bit can be obtained
            if (se.has(newMaxx ^ prefix))
            {
                maxx = newMaxx;
                break;
            }
        }

        // clear the set for next
        // iteration
        se.clear();
    }
    return maxx;
}

// Driver code
    let arr = [ 25, 10, 2, 8, 5, 3 ];
    let n = arr.length;

    document.write(max_xor(arr, n));

// This code is contributed by target_2.
</script>

Output

28

Time Complexity: 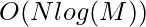, where N is the size of the array and M is the maximum number present in the array
Auxiliary Space: O(logM)

Better Approach: Another approach would be to use a Trie structure to store the bit representation of the numbers and for N terms compute the maximum XOR each can produce by going through the Trie.

C++

#include <iostream>

using namespace std;

class Node {
public:
    Node* one;
    Node* zero;
};

class trie {
    Node* root;

public:
    trie() { root = new Node(); }

    void insert(int n)
    {
        Node* temp = root;
        for (int i = 31; i >= 0; i--) {
            int bit = (n >> i) & 1;
            if (bit == 0) {
                if (temp->zero == NULL) {
                    temp->zero = new Node();
                }
                temp = temp->zero;
            }
            else {
                if (temp->one == NULL) {
                    temp->one = new Node();
                }
                temp = temp->one;
            }
        }
    }

    int max_xor_helper(int value)
    {
        Node* temp = root;
        int current_ans = 0;

        for (int i = 31; i >= 0; i--) {
            int bit = (value >> i) & 1;
            if (bit == 0) {
                if (temp->one) {
                    temp = temp->one;
                    current_ans += (1 << i);
                }
                else {
                    temp = temp->zero;
                }
            }
            else {
                if (temp->zero) {
                    temp = temp->zero;
                    current_ans += (1 << i);
                }
                else {
                    temp = temp->one;
                }
            }
        }
        return current_ans;
    }

    int max_xor(int arr[], int n)
    {
        int max_val = 0;
        insert(arr[0]);
        for (int i = 1; i < n; i++) {
            max_val = max(max_xor_helper(arr[i]), max_val);
            insert(arr[i]);
        }
        return max_val;
    }
};

int main()
{
    int input[] = { 25, 10, 2, 8, 5, 3 };
    int n = sizeof(input) / sizeof(int);
    trie t;
    cout << t.max_xor(input, n);

    return 0;
}

Java

// Java code for the above approach
import java.io.*;

class GFG {

  static class Node {
    public Node one, zero;
  }

  static class trie {
    Node root;
    public trie() { root = new Node(); }

    public void insert(int n)
    {
      Node temp = root;
      for (int i = 31; i >= 0; i--) {
        int bit = (n >> i) & 1;
        if (bit == 0) {
          if (temp.zero == null) {
            temp.zero = new Node();
          }
          temp = temp.zero;
        }
        else {
          if (temp.one == null) {
            temp.one = new Node();
          }
          temp = temp.one;
        }
      }
    }

    public int max_xor_helper(int value)
    {
      Node temp = root;
      int current_ans = 0;
      for (int i = 31; i >= 0; i--) {
        int bit = (value >> i) & 1;
        if (bit == 0) {
          if (temp.one != null) {
            temp = temp.one;
            current_ans += (1 << i);
          }
          else {
            temp = temp.zero;
          }
        }
        else {
          if (temp.zero != null) {
            temp = temp.zero;
            current_ans += (1 << i);
          }
          else {
            temp = temp.one;
          }
        }
      }
      return current_ans;
    }

    public int max_xor(int[] arr, int n)
    {
      int max_val = 0;
      insert(arr[0]);
      for (int i = 1; i < n; i++) {
        max_val = Math.max(max_xor_helper(arr[i]),
                           max_val);
        insert(arr[i]);
      }
      return max_val;
    }
  }

  public static void main(String[] args)
  {
    int[] input = { 25, 10, 2, 8, 5, 3 };
    int n = input.length;
    trie t = new trie();
    System.out.print(t.max_xor(input, n));
  }
}

// This code is contributed by lokeshmvs21.

Python3

class TrieNode :
    def __init__(self):
        self.children = {}

class Trie :
    def __init__(self) :
        self.root = TrieNode()

    def insert(self, n) :
        temp = self.root
        i = 31
        while i >= 0 :
            bit = (n >> i) & 1
            if bit not in temp.children:
                temp.children[bit] = TrieNode()
            temp = temp.children[bit]
            i -= 1

    def max_xor_helper(self, value) :
        temp = self.root
        current_ans = 0
        i = 31
        while i >= 0:
            bit = (value >> i) & 1
            if bit^1 in temp.children:
                temp = temp.children[bit^1]
                current_ans += (1 << i)
            else:
                temp = temp.children[bit]
            i -= 1
        return current_ans

class Solution:
    def solve(self, A):
        trie = Trie()
        max_val = 0
        trie.insert(A[0])
        for n in A[1:]:
            max_val = max(trie.max_xor_helper(n),max_val)
            trie.insert(n)
        return max_val

if __name__=="__main__":
  A = [25, 10, 2, 8, 5, 3]
  print(Solution().solve(A))

C#

using System;
using System.Collections.Generic;

public class GFG {

  public class Node {
    public Node one;
    public Node zero;
  };

  public class trie {
    public Node root;
    public trie() { root = new Node(); }

    public void insert(int n)
    {
      Node temp = root;
      for (int i = 31; i >= 0; i--) {
        int bit = (n >> i) & 1;
        if (bit == 0) {
          if (temp.zero == null) {
            temp.zero = new Node();
          }
          temp = temp.zero;
        }
        else {
          if (temp.one == null) {
            temp.one = new Node();
          }
          temp = temp.one;
        }
      }
    }

    public int max_xor_helper(int value)
    {
      Node temp = root;
      int current_ans = 0;

      for (int i = 31; i >= 0; i--) {
        int bit = (value >> i) & 1;
        if (bit == 0) {
          if (temp.one != null) {
            temp = temp.one;
            current_ans += (1 << i);
          }
          else {
            temp = temp.zero;
          }
        }
        else {
          if (temp.zero != null) {
            temp = temp.zero;
            current_ans += (1 << i);
          }
          else {
            temp = temp.one;
          }
        }
      }
      return current_ans;
    }

    public int max_xor(int[] arr, int n)
    {
      int max_val = 0;
      insert(arr[0]);
      for (int i = 1; i < n; i++) {
        max_val = Math.Max(max_xor_helper(arr[i]),
                           max_val);
        insert(arr[i]);
      }
      return max_val;
    }
  };

  static public void Main()
  {
    int[] input = { 25, 10, 2, 8, 5, 3 };
    int n = input.Length;
    trie t = new trie();
    Console.WriteLine(t.max_xor(input, n));
  }
}

// This code is contributed by akashish__

Javascript

class TrieNode{
    constructor(){
        this.children ={}
    }
}

class Trie{
    constructor(){
        this.root = new TrieNode();
    }
    insert(n){
        let temp = this.root;
        let i = 31;
        while(i >= 0){
            const bit = (n >> i) & 1;
            if (!temp.children[bit]) temp.children[bit] = new TrieNode()
            temp = temp.children[bit]
            i -= 1
        }
    }
    max_xor_helper(value){
        let temp = this.root;
        let current_ans = 0;
        let i = 31;
        while (i >= 0){
            const bit = (value >> i) & 1;
            if (temp.children[bit^1]){
                temp = temp.children[bit^1]
                current_ans += (1 << i)
            }
            else temp = temp.children[bit]
            i -= 1
        }
        return current_ans
    }
}

function solve(A){
    let trie = new Trie();
    let max_val = 0;
    trie.insert(A[0])
    let i = 1;
    const n = A.length;
    while(i < n){
        max_val = Math.max(trie.max_xor_helper(A[i]),max_val);
        trie.insert(A[i]);
        i += 1;
    }
    return max_val
}

const A = [25, 10, 2, 8, 5, 3]
console.log(solve(A))

Output

28

Complexity analysis:

The time complexity of inserting a single element into the trie is O( log(maximum element in array) ). Thus, for n elements, the time complexity of building the trie is O( n log(maximum element in array) ).

The time complexity of finding the maximum XOR for a single element in the trie is also O( log(maximum element in array) ). Thus, for n elements, the time complexity of finding the maximum XOR is O( n log(maximum element in array) ).

The space complexity of the trie is O( n log(maximum element in array) ). This is because in the worst case scenario, every bit of every element in the array needs to be stored in the trie. Since the maximum number of bits in an integer is log(maximum element in array), the space complexity is O( n log(maximum element in array) ).