Maximum value of B less than A such that A ^ B = A + B

Given an integer A, the task is to find the maximum value possible(B) which is less than A, such that xor of these two numbers A and B are equal to their sum, that is A ^ B = A + B.

Examples:

Input: A = 4 
Output: 3 
Explanation:
There are many such integers, such that A ^ B = A + B 
Some of these integers are – 
4 ^ 3 = 4 + 3 = 7 
4 ^ 2 = 4 + 2 = 6 
4 ^ 1 = 4 + 1 = 5 
4 ^ 0 = 4 + 0 = 4 
The maximum of these values is 3

Input: 7 
Output: 0 
There is no integer except 0 such that A + B = A ^ B 

Approach: The idea is to use the fact that 

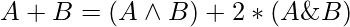and to get the value of 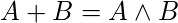, the value of (A & B) must be equal to 0.   

=> A & B = 0
=> B = ~A

For Example:

A = 4 (1 0 0)  
B = ~ A = (0 1 1) = 3 

 Below is the implementation of the above approach:

C++

// C++ implementation to find
// maximum value of B such that
// A ^ B = A + B
#include <bits/stdc++.h>
using namespace std;

// Function to find the maximum
// value of B such that A^B = A+B
void maxValue(int a)
{

    // Binary Representation of A
    string c = bitset<3>(a).to_string();
    string b = "";

    // Loop to find the negation
    // of the integer A
    for(int i = 0; i < c.length(); i++)
    {
        if ((c[i] - '0') == 1)
            b += '0';
        else
            b += '1';
    }

    // Output
    cout << bitset<3>(b).to_ulong();
}

// Driver code
int main()
{
    int a = 4;

    // Function Call
    maxValue(a);

    return 0;
}

// This code is contributed by divyeshrabadiya07

Java

// Java implementation to find
// maximum value of B such that
// A ^ B = A + B

// Function to find the maximum
// value of B such that A^B = A+B
class GFG
{

static void maxValue(int a)
{

    // Binary Representation of A
    String c = Integer.toBinaryString(a);

    String b = "";

    // Loop to find the negation
    // of the integer A
    for (int i = 0; i < c.length(); i++)
    {
        if((c.charAt(i)-'0')==1)
            b +='0';
        else
            b+='1';
    }

    // output
    System.out.print(Integer.parseInt(b, 2));

}

// Driver Code
public static void main(String []args)
{
    int a = 4;

    // Function Call
    maxValue(a);
}
}

// This code is contributed by chitranayal

Python3

# Python3 implementation to find
# maximum value of B such that
# A ^ B = A + B

# Function to find the maximum
# value of B such that A^B = A+B
def maxValue(a):

    # Binary Representation of A
    a = bin(a)[2:]

    b = ''

    # Loop to find the negation
    # of the integer A
    for i in list(a):
        b += str(int(not int(i)))

    # output
    print(int(b, 2))
    return int(b, 2)

# Driver Code
if __name__ == '__main__':
    a = 4

    # Function Call
    maxValue(a)

C#

// C# implementation to find
// maximum value of B such that
// A ^ B = A + B

// Function to find the maximum
// value of B such that A^B = A+B
using System;
using System.Collections.Generic;

class GFG
{

static void maxValue(int a)
{

    // Binary Representation of A
    String c = Convert.ToString(a, 2);

    String b = "";

    // Loop to find the negation
    // of the integer A
    for (int i = 0; i < c.Length; i++)
    {
        if((c[i] - '0') == 1)
            b += '0';
        else
            b += '1';
    }

    // output
    Console.Write(Convert.ToInt32(b, 2));

}

// Driver Code
public static void Main(String []args)
{
    int a = 4;

    // Function Call
    maxValue(a);
}
}

// This code is contributed by 29AjayKumar

Javascript

<script>

// Javascript implementation to find
// maximum value of B such that
// A ^ B = A + B

// Function to find the maximum
// value of B such that A^B = A+B
function maxValue(a)
{

    // Binary Representation of A
    var c = a.toString(2);
    var b = "";

    // Loop to find the negation
    // of the integer A
    for(var i = 0; i < c.length; i++)
    {
        if ((c[i] - '0') == 1)
            b += '0';
        else
            b += '1';
    }

    // Output
    document.write(parseInt(b,2));
}

// Driver code
var a = 4;

// Function Call
maxValue(a);
</script>

Output:

3

Performance Analysis:

• Time Complexity: In the above-given approach, there is the conversion from decimal to binary which takes O(logN) time in the worst case. Therefore, the time complexity for this approach will be O(logN).
• Auxiliary Space Complexity: In the above-given approach, there is no extra space used. Therefore, the auxiliary space complexity for the above approach will be O(1)