Maximizing the elements with a[i+1] > a[i]
Given an array of N integers, rearrange the array elements such that the next array element is greater than the previous element (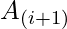
> 
).
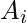Examples:
Input : arr[] = {20, 30, 10, 50, 40}
Output : 4
We rearrange the array as 10, 20, 30, 40, 50. As 20 > 10, 30 > 20, 40 > 30, 50 > 40, so we get 4 indices i such that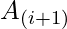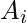Input : arr[] = {200, 100, 100, 200}
Output : 2
We get optimal arrangement as 100 200 100 200.
If all elements are distinct, then answer is simply n-1 where n is the number of elements in the array. If there are repeating elements, then answer is n – max_freq.
C++
#include<bits/stdc++.h>using namespace std; // returns the number of positions where A(i + 1) is// greater than A(i) after rearrangement of the arrayint countMaxPos(int arr[], int n){ // Creating a HashMap containing char // as a key and occurrences as a value unordered_map<int, int> map; for (int i = 0; i < n; i++ ) { if (map.count(arr[i])) map.insert({arr[i], (map.count(arr[i]) + 1)}); else map.insert({arr[i], 1}); } // Find the maximum frequency int max_freq = 0; for (auto i : map) { if (max_freq < i.second) { max_freq = i.second; } } return n - max_freq;} // Driver codeint main(){ int arr[] = { 20, 30, 10, 50, 40 }; int n = sizeof(arr)/sizeof(arr[0]); cout << (countMaxPos(arr, n));} // This code is contributed by Rajput-Ji |
Java
import java.util.*; class GFG { // returns the number of positions where A(i + 1) is // greater than A(i) after rearrangement of the array static int countMaxPos(int[] arr) { int n = arr.length; // Creating a HashMap containing char // as a key and occurrences as a value HashMap<Integer, Integer> map = new HashMap<Integer, Integer>(); for (int x : arr) { if (map.containsKey(x)) map.put(x, map.get(x) + 1); else map.put(x, 1); } // Find the maximum frequency int max_freq = 0; for (Map.Entry entry : map.entrySet()) max_freq = Math.max(max_freq, (int)entry.getValue()); return n - max_freq; } // Driver code public static void main(String[] args) { int[] arr = { 20, 30, 10, 50, 40 }; System.out.println(countMaxPos(arr)); }} |
Python3
# Python3 implementation of the above approach # Returns the number of positions where # A(i + 1) is greater than A(i) after # rearrangement of the array def countMaxPos(arr): n = len(arr) # Creating a HashMap containing char # as a key and occurrences as a value Map = {} for x in arr: if x in Map: Map[x] += 1 else: Map[x] = 1 # Find the maximum frequency max_freq = 0 for entry in Map: max_freq = max(max_freq, Map[entry]) return n - max_freq # Driver code if __name__ == "__main__": arr = [20, 30, 10, 50, 40] print(countMaxPos(arr)) # This code is contributed by Rituraj Jain |
C#
// C# implementation of the approachusing System;using System.Collections.Generic; class GFG { // returns the number of positions where // A(i + 1) is greater than A(i) after // rearrangement of the array static int countMaxPos(int[] arr) { int n = arr.Length; // Creating a HashMap containing char // as a key and occurrences as a value Dictionary<int, int> map = new Dictionary<int, int>(); foreach (int x in arr) { if (map.ContainsKey(x)) map[x] = map[x] + 1; else map.Add(x, 1); } // Find the maximum frequency int max_freq = 0; foreach(KeyValuePair<int, int> entry in map) max_freq = Math.Max(max_freq, entry.Value); return n - max_freq; } // Driver code public static void Main(String[] args) { int[] arr = { 20, 30, 10, 50, 40 }; Console.WriteLine(countMaxPos(arr)); }} // This code is contributed by 29AjayKumar |
Output:
4
