Maximize the total profit of all the persons

There is a hierarchical structure in an organization. A party is to be organized. No two immediate subordinates can come to the party. A profit is associated with every person. You have to maximize the total profit of all the persons who come to the party.

Hierarchical Structure
In a hierarchical organization, all employees(except the one at the head) are subordinates of some other employee. 
Employees only directly report to their immediate superior. This allows for a flexible and efficient structure.

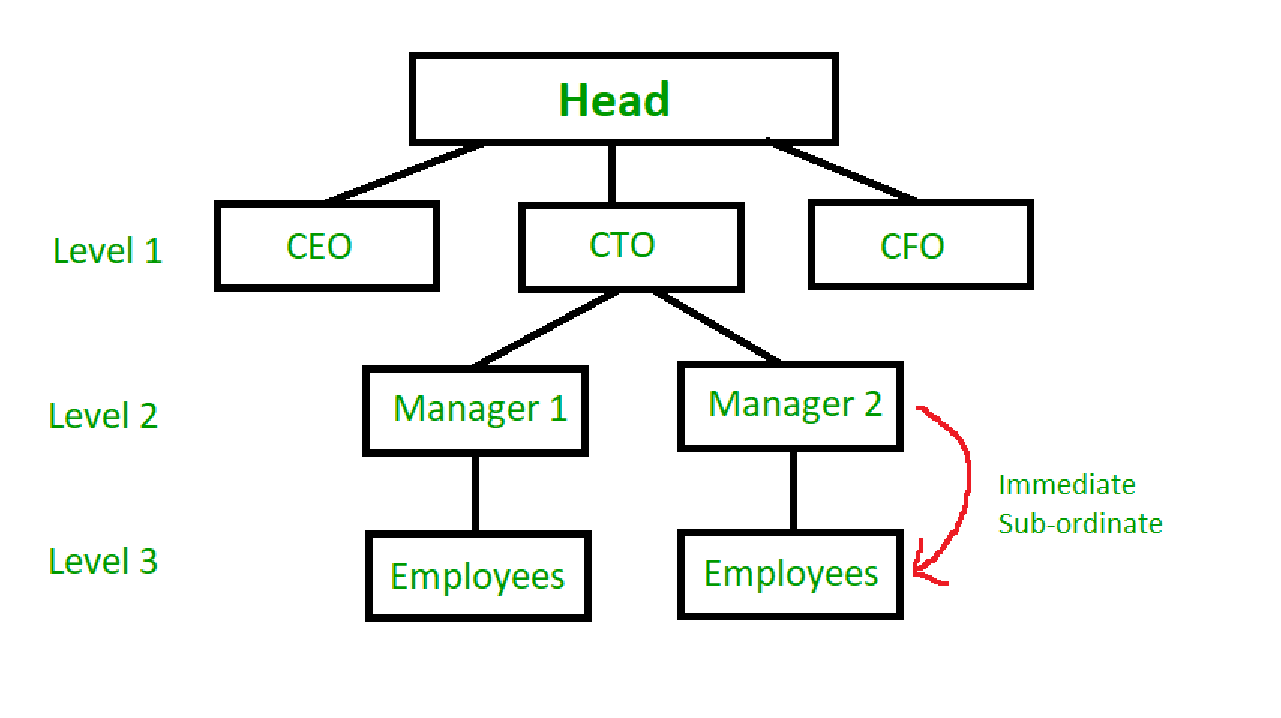
For purposes of this problem, this structure may be imagined as a tree, with each employee as its node.

Examples: 

Input: 
         15
       /   \
     10     12
    /  \   /  \
   26   4 7    9
Output: The Maximum Profit would be 15+12+26+9 = 62
The Parent 15 chooses sub-ordinate 12, 10 chooses 26 and 12 chooses 9.

Input:
        12
       / | \
      9 25 16
     /     / \
    13    13   9
Output: 12+25+13+13 = 63

Approach: Given the profit from each employee, we have to find the maximum sum such that no two employees(Nodes) with the same superior(Parent) are invited. This can be achieved if each employee selects the subordinate with the maximum contribution to go. 

In the program, the hierarchy of the company is implemented in the form of a dictionary, with the key being a unique employee ID, and data being an array of the form [Profit associated with this employ, [List of immediate Sub-ordinates]]. 

For each Employee, the subordinate with the highest profit associated is added to the total profit. Further, the Employee at the head is always invited.

Implementation:

C++

// C++ program for above approach
#include <bits/stdc++.h>
using namespace std;

int getMaxProfit(vector<vector<int> > hier)
{

    // The head has no competition and therefore invited
    int totSum = hier[0][0];
    for (vector<int> i : hier) {
        vector<int> currentSuperior = i;
        int selectedSub = 0;

        // Select the subordinate with maximum
        // value of each superior
        for (int j = 1; j < currentSuperior.size(); j++) {
            int e = currentSuperior[j];
            if (hier[e - 1][0] > selectedSub) {
                selectedSub = hier[e - 1][0];
            }
        }

        totSum += selectedSub;
    }

    return totSum;
}

// Driver Code
int main()
{

    // Define the Organization as a 2 - D array
    // Index : [Profit, List of Employees]
    /*
     Same as example 1 given above
              1:15
            /     \
          2:10    3:12
         /   \    /   \
       4:26 5:4 6:7  7:9
    */

    // Given input
    vector<vector<int> > organization
        = { { 15, 2, 3 }, { 10, 4, 5 }, { 12, 6, 7 },
            { 26 },       { 4 },        { 7 },
            { 9 } };

    // Function call
    int maxProfit = getMaxProfit(organization);
    cout << maxProfit << "\n";

    return 0;
}

Java

// Java program for above approach
class GFG {
    static int getMaxProfit(int[][] hier)
    {

        // The head has no competition and therefore invited
        int totSum = hier[0][0];
        for (int i = 0; i < hier.length; i++) {
            int selectedSub = 0;
            for (int j = 1; j < hier[i].length; j++) {

                int e = hier[i][j];
                if (hier[e - 1][0] > selectedSub) {
                    selectedSub = hier[e - 1][0];
                }
            }
            totSum += selectedSub;
        }
        return totSum;
    }

    public static void main(String[] args)
    {
        // Define the Organization as a 2 - D array
        // Index : [Profit, List of Employees]
        /*
         Same as example 1 given above
                  1:15
                /     \
              2:10    3:12
             /   \    /   \
           4:26 5:4 6:7  7:9
        */

        // Given input
        int[][] organization
            = { { 15, 2, 3 }, { 10, 4, 5 }, { 12, 6, 7 },
                { 26 },       { 4 },        { 7 },
                { 9 } };

        // Function call
        int maxProfit = getMaxProfit(organization);
        System.out.println(maxProfit);
    }
}

// This code is contributed by rajsanghavi9.

Python3

# Python program for above approach


def getMaxProfit(hier):
    # The head has no competition and therefore invited
    totSum = hier[1][0]
    for i in hier:
        currentSuperior = hier[i]
        selectedSub = 0
        # select the subordinate with maximum
        # value of each superior
        for j in currentSuperior[1]:
            if(hier[j][0] > selectedSub):
                selectedSub = hier[j][0]
        totSum += selectedSub
    return totSum

# driver function


def main():
    # Define the Organization as a Dictionary
    # Index : [Profit, List of Employees]
        # Same as example 1 given above
    # 1:15
    #       /     \
    # 2:10    3:12
    #    /   \    /   \
    # 4:26 5:4 6:7  7:9

    organization = {1: [15, [2, 3]],
                    2: [10, [4, 5]], 3: [12, [6, 7]],
                    4: [26, []], 5: [4, []], 6: [7, []], 7: [9, []]}
    maxProfit = getMaxProfit(organization)
    print(maxProfit)


main()

C#

// C# code to implement the approach
using System;
using System.Collections.Generic;

public class GFG {

    // Driver Code
    public static void Main(string[] args)
    {

        int[][] organization = new int[7][];
        organization[0] = new int[] { 15, 2, 3 };
        organization[1] = new int[] { 10, 4, 5 };
        organization[2] = new int[] { 12, 6, 7 };
        organization[3] = new int[] { 26 };
        organization[4] = new int[] { 4 };
        organization[5] = new int[] { 7 };
        organization[6] = new int[] { 9 };

        int totSum = organization[0][0];
        for (int i = 0; i < organization.Length; i++) {
            int selectedSub = 0;
            for (int j = 1; j < organization[i].Length;
                 j++) {
                int e = organization[i][j];
                if (organization[e - 1][0] > selectedSub) {
                    selectedSub = organization[e - 1][0];
                }
            }
            totSum += selectedSub;
        }

        int maxProfit = totSum;
        Console.Write(maxProfit);
    }
}

Javascript

// JS code

function getMaxProfit(hier) {
  // The head has no competition and therefore invited
  let totSum = hier[0][0];
  for (let i of hier) {
    let currentSuperior = i;
    let selectedSub = 0;

    // Select the subordinate with maximum
    // value of each superior
    for (let j = 1; j < currentSuperior.length; j++) {
      let e = currentSuperior[j];
      if (hier[e - 1][0] > selectedSub) {
        selectedSub = hier[e - 1][0];
      }
    }

    totSum += selectedSub;
  }

  return totSum;
}

// Driver Code

// Define the Organization as a 2 - D array
// Index : [Profit, List of Employees]
/*
 Same as example 1 given above
          1:15
        /     \
      2:10    3:12
     /   \    /   \
   4:26 5:4 6:7  7:9
*/

// Given input
let organization = [
  [15, 2, 3],
  [10, 4, 5],
  [12, 6, 7],
  [26],
  [4],
  [7],
  [9],
];

// Function call
let maxProfit = getMaxProfit(organization);
console.log(maxProfit);

Output

62

Complexity Analysis:

• Time Complexity: O(N)
• Auxiliary Space: O(N)