Maximize score to fill Matrix when score of a step is count of adjacent filled cells
Last Updated :
23 Jan, 2023
Given two integers N and M that denotes the number of rows and columns of a matrix that is initially empty, the task is to fill all the empty cells and find the maximum score while filling them when the score to fill a cell is the same as the count of adjacent filled cells.
Examples:
Input: N=2, M=3
Output: 7
Explanation: Matrix after applying 3 operations:

Matrix after applying three operations
Till 3 operations sum is zero. Because each cell having 1 as element has no adjacent cell having element 1. Matrix after 3 more operations:
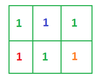
Matrix in 4th, 5th and 6th operation
4th Cell has element 1 in red color has 2 adjacent cells(up and right) having 1 . Score till here is 2.
2nd Cell has element 1 in blue color has 3 adjacent cells(left, right, down) having 1. Score till here is 2+3=5.
6th Cell has element 1 in Orange color has 2 adjacent cells(left, up) having 1. Score till here is 5+2=7.
Hence, Total maximum score that can obtain is 7.
Input: N = 5, M = 7
Output: 58
Approach: The problem can be solved based on the following idea:
Put 1 on cells of matrix in such a way that it looks like chessboard of elements 1 and empty cells. Then just put 1 at empty cells and count adjacent cell having 1. For more clarification, See the illustration of approach below.
Illustration of approach:
If N = 4, M = 4
initially Matrix will be:

Initial matrix
For making chessboard like pattern of 1, Both the index of matrix should be odd or even. On traversing process on matrix we will skip these cells, Because they are not contributing in increasing score. After applying 8 operations and making matrix like chessboard of element 1:
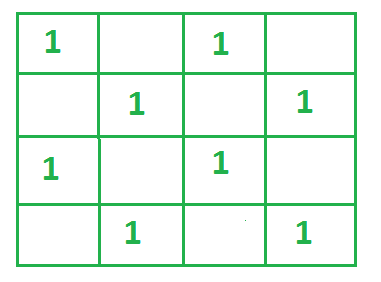
Matrix applying 8 operations(from 1 to 8)
Now, make 8 more operations one by one, put 1 at empty cells of matrix and count number of adjacent elements while putting 1 in each of these operations.
In image below next 8 operations are shown and adjacent cells are showed by arrows.

matrix after applying more 8 operations(from 9 to 16)
In the image above, 8 black 1s are put one by one in operations from 9 to 16 and adjacent cells are represented by arrows. Formally, Each arrow can be considered as 1 score, There are total 24 arrows. Hence 4*4 matrix will have maximum possible score as 24, in exactly 16 operations.

Observations
From the above image it can be seen,
- If the empty cell is at any corner suppose (yellow color in above picture) then it will contribute 2 to total score.
- Those cells which are at borders (red cells) will contribute 3 to total score
- Rest of the cell (blue colored) will contribute 4 in total score.
Follow the below steps for applying the brute force approach.
- Traverse on the matrix using two nested Loops.
- If both indices are odd or even, Then skip those cells of the matrix.
- Initialize a variable total_sum, and add 2, 3 or 4 to total_sum by testing empty cell is at the corner, border, or at other position than these two, by using discussed approach above.
- Print value of total_sum.
Below is the implementation of the above approach.
C++
#include <bits/stdc++.h>
using namespace std;
bool is_Odd(int a, int b)
{
if ((a & 1) == 1 && (b & 1) == 1) {
return true;
}
return false;
}
bool is_Even(int a, int b)
{
if ((a & 1) != 1 && (b & 1) != 1) {
return true;
}
return false;
}
int main()
{
int n = 2, m = 3;
long total_score = 0;
if (n == 1 || m == 1) {
total_score = abs(n - m);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (is_Odd(i, j) || is_Even(i, j)) {
continue;
}
else {
if ((i == 0 && j == 0)
|| (i == (n - 1) && j == (m - 1))
|| (i == (n - 1) && j == (0))
|| (i == (0) && j == (m - 1))) {
total_score += 2;
}
else if (i == 0 || i == (n - 1) || j == 0
|| j == (m - 1)) {
total_score += 3;
}
else {
total_score += 4;
}
}
}
}
cout << (total_score);
return 0;
}
|
Java
import java.io.*;
import java.lang.*;
import java.util.*;
class GFG {
static boolean is_Odd(int a, int b)
{
if ((a & 1) == 1 && (b & 1) == 1) {
return true;
}
return false;
}
static boolean is_Even(int a, int b)
{
if ((a & 1) != 1 && (b & 1) != 1) {
return true;
}
return false;
}
public static void main(String args[])
{
int n = 2, m = 3;
long total_score = 0;
if (n == 1 || m == 1) {
total_score = Math.abs(n - m);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (is_Odd(i, j) || is_Even(i, j)) {
continue;
}
else {
if ((i == 0 && j == 0)
|| (i == (n - 1) && j == (m - 1))
|| (i == (n - 1) && j == (0))
|| (i == (0) && j == (m - 1))) {
total_score += 2;
}
else if (i == 0 || i == (n - 1)
|| j == 0 || j == (m - 1)) {
total_score += 3;
}
else {
total_score += 4;
}
}
}
}
System.out.println(total_score);
}
}
|
Python3
def is_odd(a, b):
if (a & 1) == 1 and (b & 1) == 1:
return True
return False
def is_even(a, b):
if (a & 1 != 1) and (b & 1 != 1):
return True
return False
n = 2
m = 3
total_score = 0
if n == 1 or m == 1:
total_score = abs(n-m)
for i in range(n):
for j in range(m):
if is_odd(i, j) or is_even(i, j):
continue
if ((i == 0 and j == 0) or (i == (n - 1) and j == (m - 1)) or (i == (n - 1)and j == (0))or (i == (0) and j == (m - 1))):
total_score += 2
elif (i == 0 or i == (n - 1) or j == 0 or j == (m - 1)):
total_score += 3
else:
total_score += 4
print(total_score)
|
C#
using System;
public class GFG {
static bool is_Odd(int a, int b)
{
if ((a & 1) == 1 && (b & 1) == 1) {
return true;
}
return false;
}
static bool is_Even(int a, int b)
{
if ((a & 1) != 1 && (b & 1) != 1) {
return true;
}
return false;
}
static public void Main()
{
int n = 2, m = 3;
long total_score = 0;
if (n == 1 || m == 1) {
total_score = Math.Abs(n - m);
}
for (int i = 0; i < n; i++) {
for (int j = 0; j < m; j++) {
if (is_Odd(i, j) || is_Even(i, j)) {
continue;
}
else {
if ((i == 0 && j == 0)
|| (i == (n - 1) && j == (m - 1))
|| (i == (n - 1) && j == (0))
|| (i == (0) && j == (m - 1))) {
total_score += 2;
}
else if (i == 0 || i == (n - 1)
|| j == 0 || j == (m - 1)) {
total_score += 3;
}
else {
total_score += 4;
}
}
}
}
Console.WriteLine(total_score);
}
}
|
Javascript
function is_Odd(a,b)
{
if ((a & 1) == 1 && (b & 1) == 1) {
return true;
}
return false;
}
function is_Even(a,b)
{
if ((a & 1) != 1 && (b & 1) != 1) {
return true;
}
return false;
}
let n = 2, m = 3;
let total_score = 0;
if (n == 1 || m == 1) {
total_score = Math.abs(n - m);
}
for (let i = 0; i < n; i++) {
for (let j = 0; j < m; j++) {
if (is_Odd(i, j) || is_Even(i, j)) {
continue;
}
else {
if ((i == 0 && j == 0)
|| (i == (n - 1) && j == (m - 1))
|| (i == (n - 1) && j == (0))
|| (i == (0) && j == (m - 1))) {
total_score += 2;
}
else if (i == 0 || i == (n - 1) || j == 0
|| j == (m - 1)) {
total_score += 3;
}
else {
total_score += 4;
}
}
}
}
console.log(total_score);
|
Time Complexity: O(N*M)
Auxiliary Space: O(1)
Optimized approach: It can be observed that the total possible score can be obtained by using the formula:
If we create a chessboard pattern, for each row, there can be at most (M-1) pairs of adjacent cells where the values of both the cells are different. Each such pair will contribute 1 point to the final score.
So contribution from each row is (M-1). Therefore, contribution by all rows is N*(M-1).
Similarly, each column can make (N-1) pairs of adjacent cells with different values. So total contribution by all the columns will be M*(N-1).
Therefore the total possible maximum score is N*(M-1) + M*(N-1).
C++
#include <bits/stdc++.h>
using namespace std;
int main()
{
int n = 2;
int m = 3;
cout << ((n - 1) * m + n * (m - 1));
return 0;
}
|
Java
import java.io.*;
import java.lang.*;
import java.util.*;
class GFG {
public static void main(String[] args)
throws java.lang.Exception
{
int n = 2;
int m = 3;
System.out.println((n - 1) * m + n * (m - 1));
}
}
|
Python3
if __name__ == "__main__" :
n = 2;
m = 3;
print((n - 1) * m + n * (m - 1));
|
C#
using System;
public class GFG {
public static void Main(string[] args)
{
int n = 2;
int m = 3;
Console.WriteLine((n - 1) * m + n * (m - 1));
}
}
|
Javascript
let n = 2
let m = 3;
document.write((n - 1) * m + n * (m - 1));
|
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...