m-WAY Search Trees | Set-1 ( Searching )
Last Updated :
10 Jan, 2023
The m-way search trees are multi-way trees which are generalised versions of binary trees where each node contains multiple elements. In an m-Way tree of order m, each node contains a maximum of m – 1 elements and m children.
The goal of m-Way search tree of height h calls for O(h) no. of accesses for an insert/delete/retrieval operation. Hence, it ensures that the height h is close to log_m(n + 1).
The number of elements in an m-Way search tree of height h ranges from a minimum of h to a maximum of 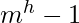 .
.
An m-Way search tree of n elements ranges from a minimum height of log_m(n+1) to a maximum of n
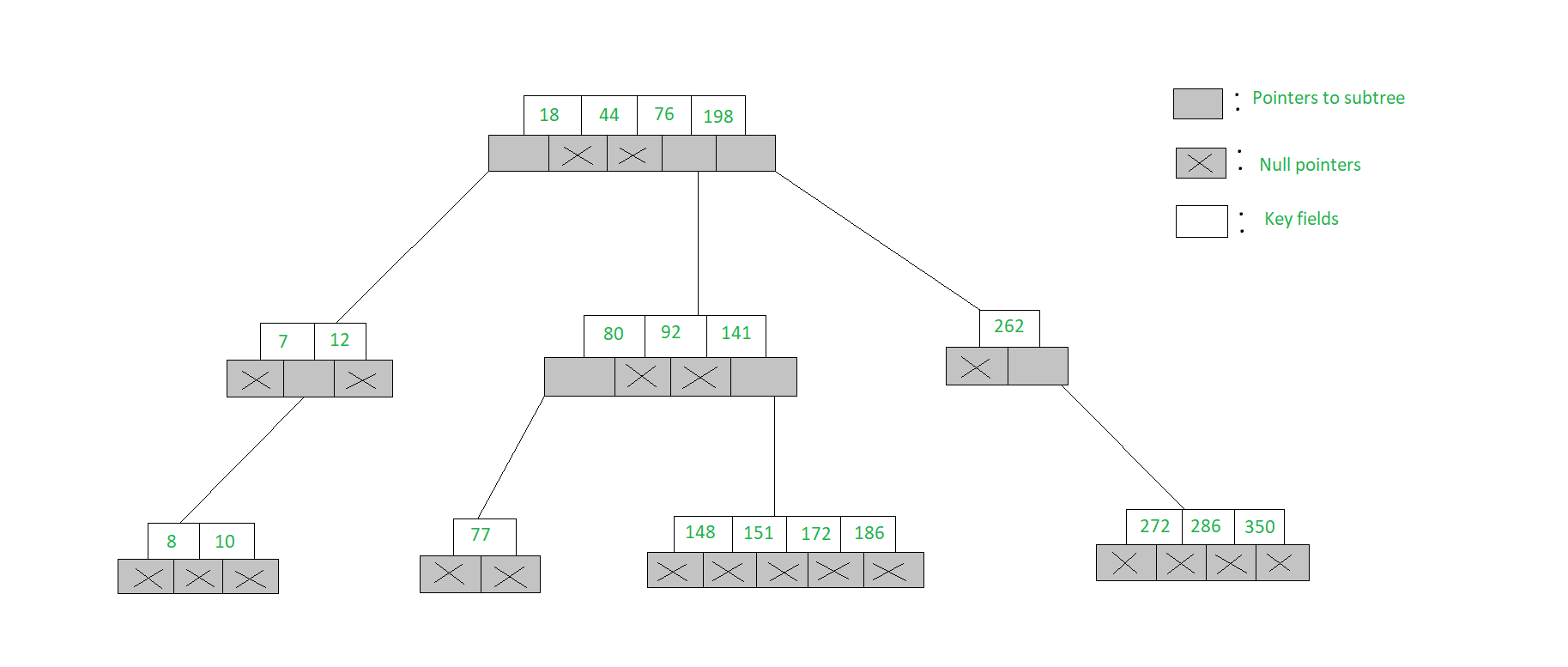
An example of a 5-Way search tree is shown in the figure below. Observe how each node has at most 5 child nodes & therefore has at most 4 keys contained in it.
The structure of a node of an m-Way tree is given below:
C++
struct node {
int count;
int value[MAX + 1];
struct node* child[MAX + 1];
};
|
Java
public class Node {
int count;
int[] value = new int[MAX + 1];
Node[] child = new Node[MAX + 1];
}
|
Python3
class node:
def __init__(self):
self.count = -1
self.value = [-1]*(MAX + 1)
self.child = [None]*(MAX + 1)
|
C#
class node {
public int count;
public int[] value = new int[MAX + 1];
public node[] child = new node[MAX + 1];
}
|
Javascript
class Node {
constructor() {
this.count = 0;
this.value = new Array(MAX + 1);
this.child = new Array(MAX + 1);
}
}
|
- Here, count represents the number of children that a particular node has
- The values of a node stored in the array value
- The addresses of child nodes are stored in the child array
- The MAX macro signifies the maximum number of values that a particular node can contain
Searching in an m-Way search tree:
- Searching for a key in an m-Way search tree is similar to that of binary search tree
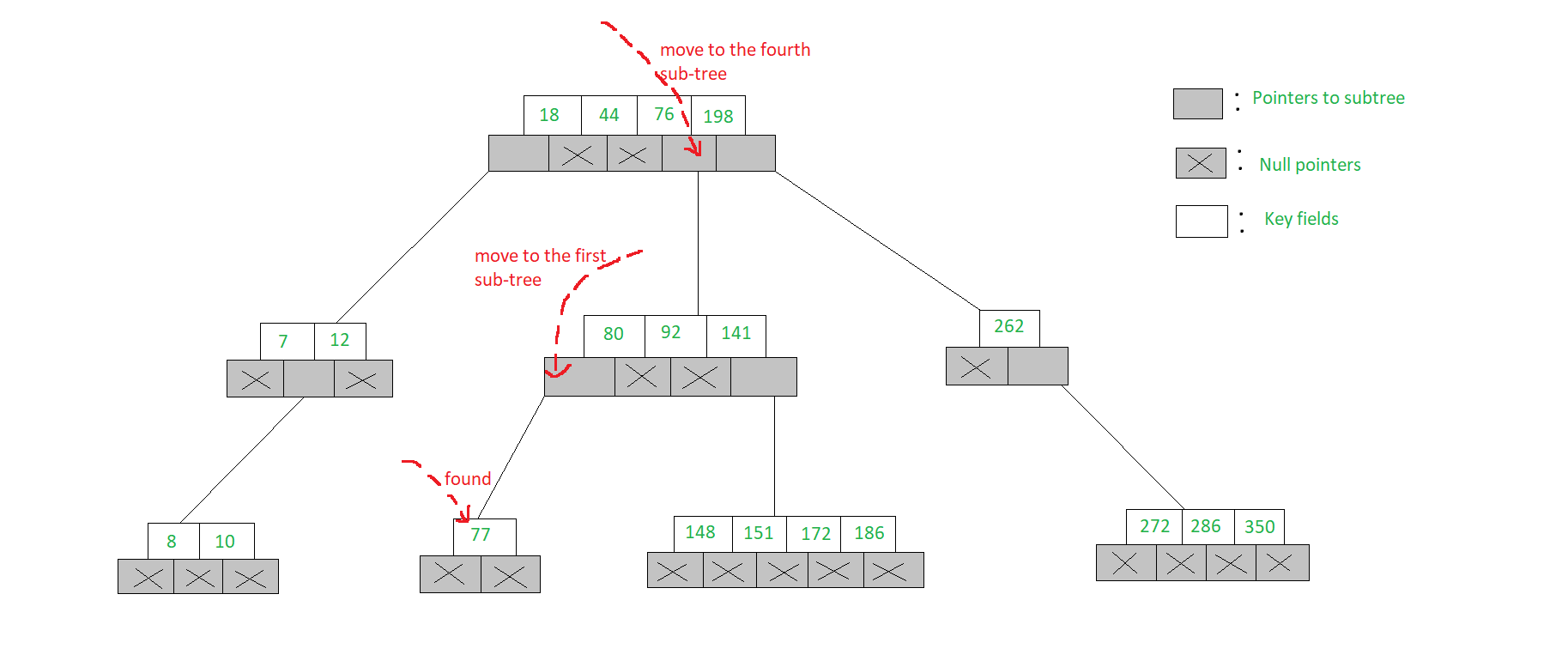
- To search for 77 in the 5-Way search tree, shown in the figure, we begin at the root & as 77> 76> 44> 18, move to the fourth sub-tree
- In the root node of the fourth sub-tree, 77< 80 & therefore we move to the first sub-tree of the node. Since 77 is available in the only node of this sub-tree, we claim 77 was successfully searched
C++
struct node* search(int val,
struct node* root,
int* pos)
{
if (root == NULL)
return NULL;
else {
if (searchnode(val, root, pos))
return root;
else
return search(val,
root->child[*pos],
pos);
}
}
int searchnode(int val,
struct node* n,
int* pos)
{
if (val < n->value[1]) {
*pos = 0;
return 0;
}
else {
*pos = n->count;
while ((val < n->value[*pos])
&& *pos > 1)
(*pos)--;
if (val == n->value[*pos])
return 1;
else
return 0;
}
}
|
Java
public Node search(int val, Node root, int pos) {
if (root == null)
return null;
else {
if (searchnode(val, root, pos))
return root;
else
return search(val, root.child[pos], pos);
}
}
public boolean searchnode(int val, Node n, int pos) {
if (val < n.value[1]) {
pos = 0;
return false;
}
else {
pos = n.count;
while ((val < n.value[pos]) && pos > 1)
pos--;
if (val == n.value[pos])
return true;
else
return false;
}
}
|
Python3
def search(val, root, pos):
if (root == None):
return None
else :
if (searchnode(val, root, pos)):
return root
else:
return search(val, root.child[pos], pos)
def searchnode(val, n, pos):
if (val < n.value[1]):
pos = 0
return 0
else :
pos = n.count
while ((val < n.value[pos]) and pos > 1):
pos-=1
if (val == n.value[pos]):
return 1
else:
return 0
|
C#
public Node search(int val, Node root, int pos)
{
if (root == null)
return null;
else {
if (searchnode(val, root, pos))
return root;
else
return search(val, root.child[pos], pos);
}
}
public bool searchnode(int val, Node n, int pos)
{
if (val < n.value[1]) {
pos = 0;
return false;
}
else {
pos = n.count;
while ((val < n.value[pos]) && pos > 1)
pos--;
if (val == n.value[pos])
return true;
else
return false;
}
}
|
Javascript
function search(val, root, pos) {
if (root === null) {
return null;
} else {
if (searchNode(val, root, pos)) {
return root;
}
else {
return search(val, root.child[pos.value], pos);
}
}
}
function searchNode(val, n, pos) {
if (val < n.value[1]) {
pos.value = 0;
return false;
}
else {
pos.value = n.count;
while (val < n.value[pos.value] && pos.value > 1) {
pos.value--;
}
if (val === n.value[pos.value]) {
return true;
} else {
return false;
}
}
}
|
search():
- The function search() receives three parameters
- The first parameter is the value to be searched, second is the address of the node from where the search is to be performed and third is the address of a variable that is used to store the position of the value once found
- Initially a condition is checked whether the address of the node being searched is NULL
- If it is, then simply a NULL value is returned
- Otherwise, a function searchnode() is called which actually searches the given value
- If the search is successful the address of the node in which the value is found is returned
- If the search is unsuccessful then a recursive call is made to the search() function for the child of the current node
searchnode():
- The function searchnode() receives three parameters
- The first parameter is the value that is to be searched
- The second parameter is the address of the node in which the search is to be performed and third is a pointer pos that holds the address of a variable in which the position of the value that once found is stored
- This function returns a value 0 if the search is unsuccessful and 1 if it is successful
- In this function initially it is checked whether the value that is to be searched is less than the very first value of the node
- If it is then it indicates that the value is not present in the current node. Hence, a value 0 is assigned in the variable that is pointed to by pos and 0 is returned, as the search is unsuccessful
Share your thoughts in the comments
Please Login to comment...