Linked List representation of Disjoint Set Data Structures
Last Updated :
15 Sep, 2023
Prerequisites : Union Find (or Disjoint Set), Disjoint Set Data Structures (Java Implementation)
A disjoint-set data structure maintains a collection S = {S1, S2,…., Sk} of disjoint dynamic sets. We identify each set by a representative, which is some member of the set. In some applications, it doesn’t matter which member is used as the representative; we care only that if we ask for the representative of a dynamic set twice without modifying the set between the requests, we get the same answer both times. Other applications may require a prespecified rule for choosing the representative, such as choosing the smallest member in the set.
Example: Determining the connected components of an undirected graph. Below figure, shows a graph with four connected components.

Solution : One procedure X that follows uses the disjoint-set operations to compute the connected components of a graph. Once X has pre-processed the graph, the procedure Y answers queries about whether two vertices are in the same connected component. Below figure shows the collection of disjoint sets after processing each edge.

See here as the above example was discussed earlier.
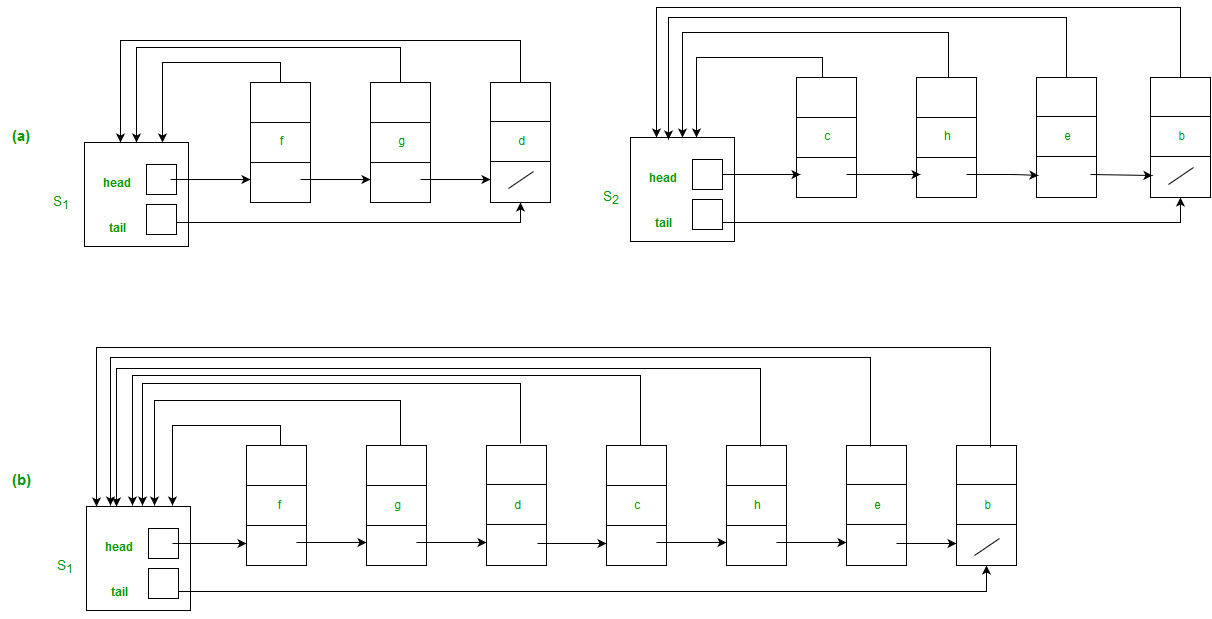
Figure
(a) Linked-list representations of two sets. Set S1 contains members d, f, and g, with representative f, and set S2 contains members b, c, e, and h, with representative c.
Each object in the list contains a set member, a pointer to the next object in the list, and a pointer back to the set object. Each set object has pointers head and tail to the first and last objects, respectively.
b) The result of UNION(e, g), which appends the linked list containing e to the linked list containing g. The representative of the resulting set is f . The set object for e’s list, S2, is destroyed.
Above three figures are taken from the Cormen(CLRS) book. Above Figure shows a simple way to implement a disjoint-set data structure: each set is represented by its own linked list. The object for each set has attributes head, pointing to the 1st object in the list, and tail, pointing to the last object.
Each object in the list contains a set member, a pointer to the next object in the list, and a pointer back to the set object. Within each linked list, the objects may appear in any order. The representative is the set member in the 1st object in the list. To carry out MAKE-SET (x), we create a new linked list whose only object is x. For FIND-SET(x), we just follow the pointer from x back to its set object and then return the member in the object that head points to. For example, in the Figure, the call FIND-SET(g) would return f.
Algorithm:
Letting x denote an object, we wish to support the following operations:
- MAKE-SET(x) creates a new set whose only member (and thus representative) is x. Since the sets are disjoint, we require that x not already be in some other set.
- UNION (x, y) unites the dynamic sets that contain x and y, say Sx and Sy, into a new set that is the union of these two sets. We assume that the two sets are disjoint prior to the operation. The representative of the resulting set is any member of Sx U Sy, although many implementations of UNION specifically choose the representative of either Sx or Sy as the new representative. Since we require the sets in the collection to be disjoint, conceptually we destroy sets Sx and Sy, removing them from the collection S. In practice, we often absorb the elements of one of the sets into the other set.
- FIND-SET(x) returns a pointer to the representative of the (unique) set containing x.
Based on the above explanation, below are implementations:
CPP
#include <bits/stdc++.h>
using namespace std;
struct Item;
struct Node
{
int val;
Node *next;
Item *itemPtr;
};
struct Item
{
Node *hd, *tl;
};
class ListSet
{
private:
unordered_map<int, Node *> nodeAddress;
public:
void makeset(int a);
Item* find(int key);
void Union(Item *i1, Item *i2);
};
void ListSet::makeset(int a)
{
Item *newSet = new Item;
newSet->hd = new Node;
newSet->tl = newSet->hd;
nodeAddress[a] = newSet->hd;
newSet->hd->val = a;
newSet->hd->itemPtr = newSet;
newSet->hd->next = NULL;
}
Item *ListSet::find(int key)
{
Node *ptr = nodeAddress[key];
return (ptr->itemPtr);
}
void ListSet::Union(Item *set1, Item *set2)
{
Node *cur = set2->hd;
while (cur != 0)
{
cur->itemPtr = set1;
cur = cur->next;
}
(set1->tl)->next = set2->hd;
set1->tl = set2->tl;
delete set2;
}
int main()
{
ListSet a;
a.makeset(13);
a.makeset(25);
a.makeset(45);
a.makeset(65);
cout << "find(13): " << a.find(13) << endl;
cout << "find(25): "
<< a.find(25) << endl;
cout << "find(65): "
<< a.find(65) << endl;
cout << "find(45): "
<< a.find(45) << endl << endl;
cout << "Union(find(65), find(45)) \n";
a.Union(a.find(65), a.find(45));
cout << "find(65]): "
<< a.find(65) << endl;
cout << "find(45]): "
<< a.find(45) << endl;
return 0;
}
|
Java
import java.util.*;
class Node {
int val;
Node next;
Item itemPtr;
}
class Item {
Node hd, tl;
}
public class ListSet {
private Map<Integer, Node> nodeAddress
= new HashMap<>();
public void makeset(int a)
{
Item newSet = new Item();
newSet.hd = new Node();
newSet.tl = newSet.hd;
nodeAddress.put(a, newSet.hd);
newSet.hd.val = a;
newSet.hd.itemPtr = newSet;
newSet.hd.next = null;
}
public Item find(int key)
{
Node ptr = nodeAddress.get(key);
return ptr.itemPtr;
}
public void Union(Item set1, Item set2)
{
Node cur = set2.hd;
while (cur != null) {
cur.itemPtr = set1;
cur = cur.next;
}
set1.tl.next = set2.hd;
set1.tl = set2.tl;
set2 = null;
}
public static void main(String[] args)
{
ListSet a = new ListSet();
a.makeset(13);
a.makeset(25);
a.makeset(45);
a.makeset(65);
System.out.println("find(13): " + a.find(13).hashCode());
System.out.println("find(25): " + a.find(25).hashCode());
System.out.println("find(65): " + a.find(65).hashCode());
System.out.println("find(45): " + a.find(45).hashCode()
+ "\n");
System.out.println("Union(find(65), find(45))");
a.Union(a.find(65), a.find(45));
System.out.println("find(65): " + a.find(65).hashCode());
System.out.println("find(45): " + a.find(45).hashCode());
}
}
|
Python3
from collections import defaultdict
class Node:
def __init__(self, val, item_ptr):
self.val = val
self.item_ptr = item_ptr
self.next = None
class Item:
def __init__(self, hd, tl):
self.hd = hd
self.tl = tl
class ListSet:
def __init__(self):
self.node_address = defaultdict(lambda: None)
def makeset(self, a):
new_set = Item(Node(a, None), None)
new_set.hd.item_ptr = new_set
new_set.tl = new_set.hd
self.node_address[a] = new_set.hd
def find(self, key):
node = self.node_address[key]
return node.item_ptr
def union(self, i1, i2):
cur = i2.hd
while cur:
cur.item_ptr = i1
cur = cur.next
i1.tl.next = i2.hd
i1.tl = i2.tl
del i2
def main():
a = ListSet()
a.makeset(13)
a.makeset(25)
a.makeset(45)
a.makeset(65)
print(f"find(13): {a.find(13)}")
print(f"find(25): {a.find(25)}")
print(f"find(65): {a.find(65)}")
print(f"find(45): {a.find(45)}")
print()
print("Union(find(65), find(45))")
a.union(a.find(65), a.find(45))
print(f"find(65): {a.find(65)}")
print(f"find(45): {a.find(45)}")
if __name__ == "__main__":
main()
|
C#
using System;
using System.Collections.Generic;
class Program {
static void Main(string[] args)
{
ListSet a = new ListSet();
a.makeset(13);
a.makeset(25);
a.makeset(45);
a.makeset(65);
Console.WriteLine("find(13): "
+ a.find(13).GetHashCode());
Console.WriteLine("find(25): "
+ a.find(25).GetHashCode());
Console.WriteLine("find(65): "
+ a.find(65).GetHashCode());
Console.WriteLine(
"find(45): " + a.find(45).GetHashCode() + "\n");
Console.WriteLine("Union(find(65), find(45))");
a.Union(a.find(65), a.find(45));
Console.WriteLine("find(65): "
+ a.find(65).GetHashCode());
Console.WriteLine("find(45): "
+ a.find(45).GetHashCode());
}
}
class Node {
public int val;
public Node next;
public Item itemPtr;
}
class Item {
public Node hd, tl;
}
class ListSet {
private Dictionary<int, Node> nodeAddress
= new Dictionary<int, Node>();
public void makeset(int a)
{
Item newSet = new Item();
newSet.hd = new Node();
newSet.tl = newSet.hd;
nodeAddress.Add(a, newSet.hd);
newSet.hd.val = a;
newSet.hd.itemPtr = newSet;
newSet.hd.next = null;
}
public Item find(int key)
{
Node ptr = nodeAddress[key];
return ptr.itemPtr;
}
public void Union(Item set1, Item set2)
{
Node cur = set2.hd;
while (cur != null) {
cur.itemPtr = set1;
cur = cur.next;
}
set1.tl.next = set2.hd;
set1.tl = set2.tl;
set2 = null;
}
}
|
Javascript
class Item {
constructor() {
this.hd = null;
this.tl = null;
}
}
class Node {
constructor(val) {
this.val = val;
this.next = null;
this.itemPtr = null;
}
}
class ListSet {
constructor() {
this.nodeAddress = new Map();
}
makeset(a) {
const newSet = new Item();
newSet.hd = new Node(a);
newSet.tl = newSet.hd;
this.nodeAddress.set(a, newSet.hd);
newSet.hd.itemPtr = newSet;
newSet.hd.next = null;
}
find(key) {
const ptr = this.nodeAddress.get(key);
return ptr ? ptr.itemPtr : null;
}
Union(set1, set2) {
let cur = set2.hd;
while (cur !== null) {
cur.itemPtr = set1;
cur = cur.next;
}
set1.tl.next = set2.hd;
set1.tl = set2.tl;
set2.hd = null;
set2.tl = null;
}
}
const a = new ListSet();
a.makeset(13);
a.makeset(25);
a.makeset(45);
a.makeset(65);
console.log("find(13):", a.find(13));
console.log("find(25):", a.find(25));
console.log("find(65):", a.find(65));
console.log("find(45):", a.find(45));
console.log("\nUnion(find(65), find(45))");
a.Union(a.find(65), a.find(45));
console.log("find(65):", a.find(65));
console.log("find(45):", a.find(45));
|
Output
find(13): 0x1cf8c20
find(25): 0x1cf8ca0
find(65): 0x1cf8d70
find(45): 0x1cf8c80
Union(find(65), find(45))
find(65]): 0x1cf8d70
find(45]): 0x1cf8d70
Note: The node address will change every time, we run the program. Time complexities of MAKE-SET and FIND-SET are O(1). Time complexity for UNION is O(n).
Share your thoughts in the comments
Please Login to comment...