Last digit of a number raised to last digit of N factorial
Last Updated :
26 Apr, 2023
Given two number X and N, the task is to find the last digit of X raised to last digit of N factorial, i.e. 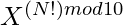 .
.
Examples:
Input: X = 5, N = 2
Output: 5
Explanation:
Since, 2! mod 10 = 2
therefore 52 = 25 and the last digit of 25 is 5.
Input: X = 10, N = 4
Output: 0
Explanation:
Since, 4! mod 10 = 24 mod 10 = 4
therefore 104 = 10000 and the last digit of 10000 is 0.
Approach: The most efficient way to solve this problem is to find any pattern in the required last digit, with the help of last digit of N! and last digit of X raised to Y
Below is the various observation of the above-given equation:
- If N = 0 or N = 1, then the last digit is 1 or
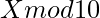 respectively.
respectively. - Since 5! is 120, therefore for N ? 5 the value of (N! mod 10) will be zero.
- Now we are left with digit 2, 3, 4. For this we have:
for N = 2,
N! mod 10 = 2! mod 10 = 2
for N = 3,
N! mod 10 = 3! mod 10 = 6
for N = 4,
N! mod 10 = 4! mod 10 = 24 mod 10 = 4
Now for X2, X4, and X6
we will check that after which nth power of Xn the value of last digit repeats,
i.e, after which nth power of last digit of Xn the value of last digit repeats.
- Below is the table for what power of the last digit from 0 to 9 in any number repeats:
| Number | Cyclicity |
|---|
| 0 | 1 |
| 1 | 1 |
| 2 | 4 |
| 3 | 4 |
| 4 | 2 |
| 5 | 1 |
| 6 | 1 |
| 7 | 4 |
| 8 | 4 |
| 9 | 2 |
Below are the steps based on the above observations:
- If X is not a multiple of 10 then divide the evaluated value of
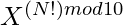 by cyclicity of the last digit of X. If remainder(say r) is 0 then do the following:
by cyclicity of the last digit of X. If remainder(say r) is 0 then do the following:
- If the last digit of X is any of 2, 4, 6, or 8 then the answer will be 6.
- If the last digit of X is any of 1, 3, 7, or 9 then the answer will be 1.
- If the last digit of X is 5 then answer will be 5.
- Else if remainder(say r) is a non-zero then answer is
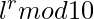 , where ‘l’ is the last digit of X.
, where ‘l’ is the last digit of X. - Else if X is a multiple of 10 then the answer will be 0 always.
Below is the implementation of the above approach:
C++
#include<bits/stdc++.h>
using namespace std;
long power(long a, long b, long c)
{
long result = 1;
while (b > 0)
{
if ((b & 1) == 1)
{
result = (result * a) % c;
}
b /= 2;
a = (a * a) % c;
}
return result;
}
long calculate(long X, long N)
{
int a[10];
int cyclicity[11];
cyclicity[1] = 1;
cyclicity[2] = 4;
cyclicity[3] = 4;
cyclicity[4] = 2;
cyclicity[5] = 1;
cyclicity[6] = 1;
cyclicity[7] = 4;
cyclicity[8] = 4;
cyclicity[9] = 2;
cyclicity[10] = 1;
if (N == 0 || N == 1)
{
return (X % 10);
}
else if (N == 2 || N == 3 || N == 4)
{
long temp = (long)1e18;
a[2] = 2;
a[3] = 6;
a[4] = 4;
long v = X % 10;
if (v != 0)
{
int u = cyclicity[(int)v];
int r = a[(int)N] % u;
if (r == 0)
{
if (v == 2 || v == 4 ||
v == 6 || v == 8)
{
return 6;
}
else if (v == 5)
{
return 5;
}
else if (v == 1 || v == 3 ||
v == 7 || v == 9)
{
return 1;
}
}
else
{
return (power(v, r, temp) % 10);
}
}
else
{
return 0;
}
}
return 1;
}
int main()
{
int X = 18;
int N = 4;
long result = calculate(X, N);
cout << result;
}
|
Java
import java.util.*;
class TestClass {
public static long power(long a, long b, long c) {
long result = 1;
while (b > 0) {
if ((b & 1) == 1) {
result = (result * a) % c;
}
b /= 2;
a = (a * a) % c;
}
return result;
}
public static long calculate(long X, long N) {
int a[] = new int[10];
int cyclicity[] = new int[11];
cyclicity[1] = 1;
cyclicity[2] = 4;
cyclicity[3] = 4;
cyclicity[4] = 2;
cyclicity[5] = 1;
cyclicity[6] = 1;
cyclicity[7] = 4;
cyclicity[8] = 4;
cyclicity[9] = 2;
cyclicity[10] = 1;
if (N == 0 || N == 1) {
return (X % 10);
}
else if (N == 2 || N == 3 || N == 4) {
long temp = (long) 1e18;
a[2] = 2;
a[3] = 6;
a[4] = 4;
long v = X % 10;
if (v != 0) {
int u = cyclicity[(int) v];
int r = a[(int) N] % u;
if (r == 0) {
if (v == 2 || v == 4 || v == 6 || v == 8) {
return 6;
}
else if (v == 5) {
return 5;
}
else if (v == 1 || v == 3 || v == 7 || v == 9) {
return 1;
}
}
else {
return (power(v, r, temp) % 10);
}
}
else {
return 0;
}
}
return 1;
}
public static void main(String args[])
throws Exception
{
int X = 18;
int N = 4;
long result = calculate(X, N);
System.out.println(result);
}
}
|
Python3
def power(a, b, c):
result = 1
while (b > 0):
if ((b & 1) == 1):
result = (result * a) % c
b //= 2
a = (a * a) % c
return result
def calculate(X, N):
a = 10 * [0]
cyclicity = 11 * [0]
cyclicity[1] = 1
cyclicity[2] = 4
cyclicity[3] = 4
cyclicity[4] = 2
cyclicity[5] = 1
cyclicity[6] = 1
cyclicity[7] = 4
cyclicity[8] = 4
cyclicity[9] = 2
cyclicity[10] = 1
if (N == 0 or N == 1):
return (X % 10)
elif (N == 2 or N == 3 or N == 4):
temp = 1e18;
a[2] = 2
a[3] = 6
a[4] = 4
v = X % 10
if (v != 0):
u = cyclicity[v]
r = a[N] % u
if (r == 0):
if (v == 2 or v == 4 or
v == 6 or v == 8):
return 6
elif (v == 5):
return 5
elif (v == 1 or v == 3 or
v == 7 or v == 9):
return 1
else:
return (power(v, r, temp) % 10)
else:
return 0
return 1
if __name__ == "__main__":
X = 18
N = 4
result = calculate(X, N)
print(result)
|
C#
using System;
using System.Collections.Generic;
class GFG{
static long power(long a, long b, long c)
{
long result = 1;
while (b > 0)
{
if ((b & 1) == 1)
{
result = (result * a) % c;
}
b /= 2;
a = (a * a) % c;
}
return result;
}
public static long calculate(long X,
long N)
{
int[] a = new int[10];
int[] cyclicity = new int[11];
cyclicity[1] = 1;
cyclicity[2] = 4;
cyclicity[3] = 4;
cyclicity[4] = 2;
cyclicity[5] = 1;
cyclicity[6] = 1;
cyclicity[7] = 4;
cyclicity[8] = 4;
cyclicity[9] = 2;
cyclicity[10] = 1;
if (N == 0 || N == 1)
{
return (X % 10);
}
else if (N == 2 || N == 3 || N == 4)
{
long temp = (long)1e18;
a[2] = 2;
a[3] = 6;
a[4] = 4;
long v = X % 10;
if (v != 0)
{
int u = cyclicity[(int)v];
int r = a[(int)N] % u;
if (r == 0)
{
if (v == 2 || v == 4 ||
v == 6 || v == 8)
{
return 6;
}
else if (v == 5)
{
return 5;
}
else if ( v == 1 || v == 3 ||
v == 7 || v == 9)
{
return 1;
}
}
else
{
return (power(v, r, temp) % 10);
}
}
else
{
return 0;
}
}
return 1;
}
static void Main()
{
int X = 18;
int N = 4;
long result = calculate(X, N);
Console.Write(result);
}
}
|
Javascript
<script>
function power(a, b, c) {
var result = 1;
while (b > 0) {
if ((b & 1) == 1) {
result = (result * a) % c;
}
b /= 2;
a = (a * a) % c;
}
return result;
}
function calculate(X, N) {
var a = [...Array(10)];
var cyclicity = [...Array(11)];
cyclicity[1] = 1;
cyclicity[2] = 4;
cyclicity[3] = 4;
cyclicity[4] = 2;
cyclicity[5] = 1;
cyclicity[6] = 1;
cyclicity[7] = 4;
cyclicity[8] = 4;
cyclicity[9] = 2;
cyclicity[10] = 1;
if (N == 0 || N == 1) {
return X % 10;
}
else if (N == 2 || N == 3 || N == 4) {
var temp = 1e18;
a[2] = 2;
a[3] = 6;
a[4] = 4;
var v = X % 10;
if (v != 0) {
var u = cyclicity[parseInt(v)];
var r = a[parseInt(N)] % u;
if (r == 0)
{
if (v == 2 || v == 4 || v == 6 || v == 8) {
return 6;
}
else if (v == 5) {
return 5;
}
else if (v == 1 || v == 3 || v == 7 || v == 9) {
return 1;
}
}
else {
return power(v, r, temp) % 10;
}
}
else {
return 0;
}
}
return 1;
}
var X = 18;
var N = 4;
var result = calculate(X, N);
document.write(result);
</script>
|
Time Complexity: O(logn) because it is using a while loop
Auxiliary Space: O(11)
Approach#2: using for loop
We can first calculate the last digit of N factorial and then take the last digit of X raised to this last digit. We can use modular arithmetic to calculate the last digit of N factorial and to take the last digit of X raised to this value.
Algorithm
1. Calculate the last digit of N factorial using modular arithmetic.
2. Calculate the last digit of X raised to this last digit using modular arithmetic.
3. Return the result.
C++
#include <cmath>
#include <iostream>
using namespace std;
int lastDigit(int X, int N)
{
int lastDigitNFactorial = 1;
for (int i = 2; i <= N; i++) {
lastDigitNFactorial
= (lastDigitNFactorial * (i % 10)) % 10;
}
int lastDigitXToLastDigitNFactorial
= (int)pow(X % 10, lastDigitNFactorial) % 10;
return lastDigitXToLastDigitNFactorial;
}
int main()
{
int X = 18;
int N = 4;
cout << lastDigit(X, N) << endl;
return 0;
}
|
Java
public class Main {
public static int lastDigit(int X, int N)
{
int lastDigitNFactorial = 1;
for (int i = 2; i <= N; i++) {
lastDigitNFactorial
= (lastDigitNFactorial * (i % 10)) % 10;
}
int lastDigitXToLastDigitNFactorial
= (int)Math.pow(X % 10, lastDigitNFactorial)
% 10;
return lastDigitXToLastDigitNFactorial;
}
public static void main(String[] args)
{
int X = 18;
int N = 4;
System.out.println(lastDigit(X, N));
}
}
|
Python3
def last_digit(X, N):
last_digit_n_factorial = 1
for i in range(2, N+1):
last_digit_n_factorial = (last_digit_n_factorial * (i % 10)) % 10
last_digit_X_to_last_digit_n_factorial = pow(
X % 10, last_digit_n_factorial, 10)
return last_digit_X_to_last_digit_n_factorial
X = 18
N = 4
print(last_digit(X, N))
|
C#
using System;
class Program {
static int lastDigit(int X, int N)
{
int lastDigitNFactorial = 1;
for (int i = 2; i <= N; i++) {
lastDigitNFactorial
= (lastDigitNFactorial * (i % 10)) % 10;
}
int lastDigitXToLastDigitNFactorial
= (int)Math.Pow(X % 10, lastDigitNFactorial)
% 10;
return lastDigitXToLastDigitNFactorial;
}
static void Main(string[] args)
{
int X = 18;
int N = 4;
Console.WriteLine(lastDigit(X, N));
}
}
|
Javascript
function last_digit(X, N) {
let last_digit_n_factorial = 1;
for (let i = 2; i <= N; i++) {
last_digit_n_factorial = (last_digit_n_factorial * (i % 10)) % 10;
}
let last_digit_X_to_last_digit_n_factorial = Math.pow(X % 10, last_digit_n_factorial) % 10;
return last_digit_X_to_last_digit_n_factorial;
}
let X = 18;
let N = 4;
console.log(last_digit(X, N));
|
Time complexity: O(N), where N is the input
Space complexity: O(1)
Share your thoughts in the comments
Please Login to comment...