Larger of a^b or b^a (a raised to power b or b raised to power a)
Last Updated :
31 Aug, 2022
Given two numbers 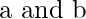 , find which is greater
, find which is greater 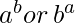 .
.
If 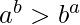 , print a^b is greater
, print a^b is greater
If 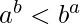 , print b^a is greater
, print b^a is greater
If 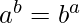 , print Both are equal
, print Both are equal
Examples:
Input : 3 5
Output : a^b is greater
3^5 = 243, 5^3 = 125. Since, 243>125, therefore a^b > b^a.
Input : 2 4
Output : Both are equal
2^4 = 16, 4^2 = 16. Since, 16=16, therefore a^b = b^a.
Brute Force solution would be to just compute 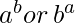 and compare them. But since
and compare them. But since  can be large enough that
can be large enough that  can not be stored even in long long int, so this solution is not feasible. Also computing to the power n would require at least
can not be stored even in long long int, so this solution is not feasible. Also computing to the power n would require at least 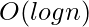 time using the fast exponentiation technique.
time using the fast exponentiation technique.
Efficient approach would be to use logarithm. We have to compare 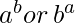 . If we take log, the problem reduces to comparing
. If we take log, the problem reduces to comparing 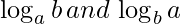 .
.
Hence,
If 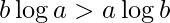 , print a^b is greater
, print a^b is greater
If 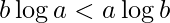 , print b^a is greater
, print b^a is greater
If 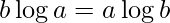 , print Both are equal
, print Both are equal
Below is the implementation of the efficient approach discussed above.
C++
#include <bits/stdc++.h>
using namespace std;
void findGreater(int a, int b)
{
long double x = (long double)a * (long double)(log((long double)(b)));
long double y = (long double)b * (long double)(log((long double)(a)));
if (y > x) {
cout << "a^b is greater" << endl;
}
else if (y < x) {
cout << "b^a is greater" << endl;
}
else {
cout << "Both are equal" << endl;
}
}
int main()
{
int a = 3, b = 5, c = 2, d = 4;
findGreater(a, b);
findGreater(c, d);
return 0;
}
|
Java
public class GFG{
static void findGreater(int a, int b)
{
double x = (double)a * (double)(Math.log((double)(b)));
double y = (double)b * (double)(Math.log((double)(a)));
if (y > x) {
System.out.println("a^b is greater") ;
}
else if (y < x) {
System.out.println("b^a is greater") ;
}
else {
System.out.println("Both are equal") ;
}
}
public static void main(String []args)
{
int a = 3, b = 5, c = 2, d = 4;
findGreater(a, b);
findGreater(c, d);
}
}
|
Python 3
import math
def findGreater(a, b):
x = a * (math.log(b));
y = b * (math.log(a));
if (y > x):
print ("a^b is greater");
elif (y < x):
print("b^a is greater");
else :
print("Both are equal");
a = 3;
b = 5;
c = 2;
d = 4;
findGreater(a, b);
findGreater(c, d);
|
C#
using System;
public class GFG{
static void findGreater(int a, int b)
{
double x = (double)a * (double)(Math.Log((double)(b)));
double y = (double)b * (double)(Math.Log((double)(a)));
if (y > x) {
Console.Write("a^b is greater\n") ;
}
else if (y < x) {
Console.Write("b^a is greater"+"\n") ;
}
else {
Console.Write("Both are equal") ;
}
}
public static void Main()
{
int a = 3, b = 5, c = 2, d = 4;
findGreater(a, b);
findGreater(c, d);
}
}
|
PHP
<?php
function findGreater($a, $b)
{
$x = (double)$a * (double)(log((double)($b)));
$y = (double)$b * (double)(log((double)($a)));
if ($y > $x)
{
echo "a^b is greater", "\n";
}
else if ($y < $x)
{
echo "b^a is greater", "\n" ;
}
else
{
echo "Both are equal", "\n" ;
}
}
$a = 3;
$b = 5;
$c = 2;
$d = 4;
findGreater($a, $b);
findGreater($c, $d);
?>
|
Javascript
<script>
function findGreater(a , b) {
var x = a * (Math.log( (b)));
var y = b * (Math.log( (a)));
if (y > x) {
document.write("a^b is greater<br/>");
} else if (y < x) {
document.write("b^a is greater<br/>");
} else {
document.write("Both are equal<br/>");
}
}
var a = 3, b = 5, c = 2, d = 4;
findGreater(a, b);
findGreater(c, d);
</script>
|
Output:
a^b is greater
Both are equal
Time Complexity: O(logn), since it is using inbuilt log function
Auxiliary Space: O(1), since no extra space has been taken.
Share your thoughts in the comments
Please Login to comment...