Knapsack Encryption Algorithm in Cryptography
Last Updated :
31 Aug, 2023
Knapsack Encryption Algorithm is the first general public key cryptography algorithm. It is developed by Ralph Merkle and Mertin Hellman in 1978. As it is a Public key cryptography, it needs two different keys. One is Public key which is used for Encryption process and the other one is Private key which is used for Decryption process. In this algorithm we will use two different knapsack problems in which one is easy and other one is hard. The easy knapsack is used as the private key and the hard knapsack is used as the public key. The easy knapsack is used to derived the hard knapsack.
For the easy knapsack, we will choose a Super Increasing knapsack problem. Super increasing knapsack is a sequence in which every next term is greater than the sum of all preceding terms.
Example –
{1, 2, 4, 10, 20, 40} is a super increasing as
1<2, 1+2<4, 1+2+4<10, 1+2+4+10<20 and 1+2+4+10+20<40.
Derive the Public key
- Step-1:
Choose a super increasing knapsack {1, 2, 4, 10, 20, 40} as the private key.
- Step-2:
Choose two numbers n and m. Multiply all the values of private key by the number n and then find modulo m. The value of m must be greater than the sum of all values in private key, for example 110. And the number n should have no common factor with m, for example 31.
- Step-3:
Calculate the values of Public key using m and n.
1x31 mod(110) = 31
2x31 mod(110) = 62
4x31 mod(110) = 14
10x31 mod(110) = 90
20x31 mod(110) = 70
40x31 mod(110) = 30
- Thus, our public key is {31, 62, 14, 90, 70, 30}
And Private key is {1, 2, 4, 10, 20, 40}.
Now take an example for understanding the process of encryption and decryption.
Example –
Lets our plain text is 100100111100101110.
1. Encryption :
As our knapsacks contain six values, so we will split our plain text in a groups of six:
100100 111100 101110
Multiply each values of public key with the corresponding values of each group and take their sum.
100100 {31, 62, 14, 90, 70, 30}
1x31+0x62+0x14+1x90+0x70+0x30 = 121
111100 {31, 62, 14, 90, 70, 30}
1x31+1x62+1x14+1x90+0x70+0x30 = 197
101110 {31, 62, 14, 90, 70, 30}
1x31+0x62+1x14+1x90+1x70+0x30 = 205
So, our cipher text is 121 197 205.
2. Decryption :
The receiver receive the cipher text which has to be decrypt. The receiver also knows the values of m and n.
So, first we need to find the 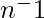 , which is multiplicative inverse of n mod m i.e.,
, which is multiplicative inverse of n mod m i.e.,
n x 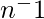 mod(m) = 131 x
mod(m) = 131 x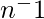 mod(110) = 1
mod(110) = 1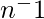 = 71
= 71
Now, we have to multiply 71 with each block of cipher text take modulo m.
121 x 71 mod(110) = 11
Then, we will have to make the sum of 11 from the values of private key {1, 2, 4, 10, 20, 40} i.e.,
1+10=11 so make that corresponding bits 1 and others 0 which is 100100.
Similarly,
197 x 71 mod(110) = 17
1+2+4+10=17 = 111100
And, 205 x 71 mod(110) = 35
1+4+10+20=35 = 101110
After combining them we get the decoded text.
100100111100101110 which is our plain text.
Example:
Here’s a Python example of the Knapsack Encryption Algorithm with proper explanation and output:
Python
import random
def generate_super_increasing_sequence(n):
sequence = [random.randint(1, 100)]
while len(sequence) < n:
next_element = sum(sequence) + random.randint(1, 10)
sequence.append(next_element)
return sequence
def generate_private_key(public_key, q, r):
private_key = [(r * element) % q for element in public_key]
return private_key
def knapsack_encrypt(plaintext, public_key):
encrypted_message = sum(public_key[i] for i in range(len(plaintext)) if plaintext[i] == '1')
return encrypted_message
def knapsack_decrypt(ciphertext, private_key, q):
r_inverse = pow(r, -1, q)
decrypted_message = ''
for element in reversed(private_key):
if (ciphertext * r_inverse) % q >= element:
decrypted_message = '1' + decrypted_message
ciphertext -= element
else:
decrypted_message = '0' + decrypted_message
return decrypted_message
if __name__ == "__main__":
n = 8
q = 103
r = 3
public_key = generate_super_increasing_sequence(n)
private_key = generate_private_key(public_key, q, r)
plaintext = "11001010"
ciphertext = knapsack_encrypt(plaintext, public_key)
decrypted_message = knapsack_decrypt(ciphertext, private_key, q)
print("Original Message:", plaintext)
print("Encrypted Ciphertext:", ciphertext)
print("Decrypted Message:", decrypted_message)
|
Explanation:
- The ‘
generate_super_increasing_sequence()' function generates a super-increasing sequence, which serves as the public key. The function starts with a random element and adds random values to it until the sequence reaches the desired length n. - The ‘
generate_private_key()' function generates the private key from the public key using the formula: ‘private_key[i] = (r * public_key[i]) % q'. - The ‘
knapsack_encrypt()' function takes the plaintext and the public key as input. It converts the plaintext to binary and encrypts it by summing the elements of the public key corresponding to ‘1’ bits in the binary representation of the plaintext. - The ‘
knapsack_decrypt()' function takes the ciphertext, private key, and modulus q as input. It uses the private key to reconstruct the original binary representation of the plaintext by finding ‘1’ bits in the ciphertext and subtracting the corresponding elements from the private key.
Output:
Original Message: 11001010
Encrypted Ciphertext: 426
Decrypted Message: 11001010
In this example, the plaintext “11001010” is encrypted using the Knapsack Encryption Algorithm, resulting in the ciphertext “426”. The ciphertext is then decrypted back to the original plaintext, which demonstrates the correctness of the algorithm.
Share your thoughts in the comments
Please Login to comment...