Java Program for Sum of squares of first n natural numbers
Last Updated :
12 Sep, 2022
Given a positive integer N. The task is to find 12 + 22 + 32 + ….. + N2.
Examples:
Input : N = 4
Output : 30
12 + 22 + 32 + 42
= 1 + 4 + 9 + 16
= 30
Input : N = 5
Output : 55
Method 1: O(N) The idea is to run a loop from 1 to n and for each i, 1 <= i <= n, find i2 to sum.
Java
import java.io.*;
class GFG {
static int squaresum(int n)
{
int sum = 0;
for (int i = 1; i <= n; i++)
sum += (i * i);
return sum;
}
public static void main(String args[]) throws IOException
{
int n = 4;
System.out.println(squaresum(n));
}
}
|
Time Complexity : O(n)
Auxiliary Space: O(1)
Method 2:
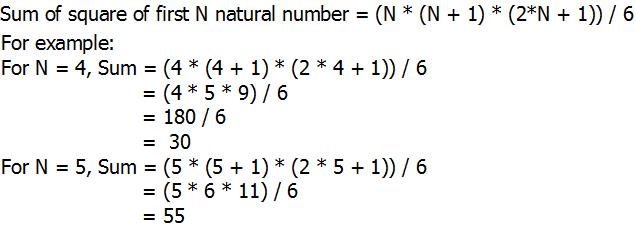
Proof:
We know,
(k + 1)3 = k3 + 3 * k2 + 3 * k + 1
We can write the above identity for k from 1 to n:
23 = 13 + 3 * 12 + 3 * 1 + 1 ......... (1)
33 = 23 + 3 * 22 + 3 * 2 + 1 ......... (2)
43 = 33 + 3 * 32 + 3 * 3 + 1 ......... (3)
53 = 43 + 3 * 42 + 3 * 4 + 1 ......... (4)
...
n3 = (n - 1)3 + 3 * (n - 1)2 + 3 * (n - 1) + 1 ......... (n - 1)
(n + 1)3 = n3 + 3 * n2 + 3 * n + 1 ......... (n)
Putting equation (n - 1) in equation n,
(n + 1)3 = (n - 1)3 + 3 * (n - 1)2 + 3 * (n - 1) + 1 + 3 * n2 + 3 * n + 1
= (n - 1)3 + 3 * (n2 + (n - 1)2) + 3 * ( n + (n - 1) ) + 1 + 1
By putting all equation, we get
(n + 1)3 = 13 + 3 * ? k2 + 3 * ? k + ? 1
n3 + 3 * n2 + 3 * n + 1 = 1 + 3 * ? k2 + 3 * (n * (n + 1))/2 + n
n3 + 3 * n2 + 3 * n = 3 * ? k2 + 3 * (n * (n + 1))/2 + n
n3 + 3 * n2 + 2 * n - 3 * (n * (n + 1))/2 = 3 * ? k2
n * (n2 + 3 * n + 2) - 3 * (n * (n + 1))/2 = 3 * ? k2
n * (n + 1) * (n + 2) - 3 * (n * (n + 1))/2 = 3 * ? k2
n * (n + 1) * (n + 2 - 3/2) = 3 * ? k2
n * (n + 1) * (2 * n + 1)/2 = 3 * ? k2
n * (n + 1) * (2 * n + 1)/6 = ? k2
Java
import java.io.*;
class GFG {
static int squaresum(int n)
{
return (n * (n + 1) * (2 * n + 1)) / 6;
}
public static void main(String args[])
throws IOException
{
int n = 4;
System.out.println(squaresum(n));
}
}
|
Avoiding early overflow:
For large n, the value of (n * (n + 1) * (2 * n + 1)) would overflow. We can avoid overflow up to some extent using the fact that n*(n+1) must be divisible by 2.
Java
import java.io.*;
import java.util.*;
class GFG {
public static int squaresum(int n)
{
return (n * (n + 1) / 2) * (2 * n + 1) / 3;
}
public static void main(String[] args)
{
int n = 4;
System.out.println(squaresum(n));
}
}
|
Time complexity: O(1) as it is doing constant operations
Auxiliary Space: O(1) as it is using constant space
Please refer complete article on Sum of squares of first n natural numbers for more details!
Share your thoughts in the comments
Please Login to comment...