Intersecting rectangle when bottom-left and top-right corners of two rectangles are given

Difficulty Level : Easy
Last Updated : 22 Apr, 2021

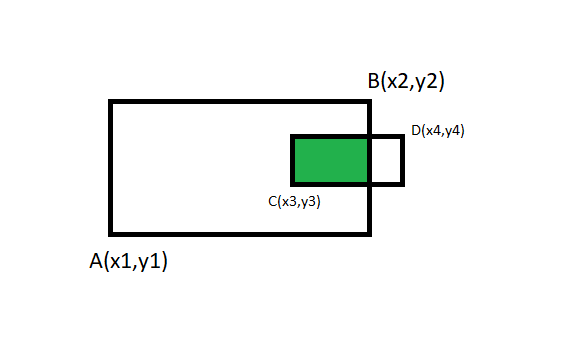
Given coordinates of 4 points, bottom-left and top-right corners of two rectangles. The task is to find the coordinates of the intersecting rectangle formed by the given two rectangles.

Examples:

Input:
rec1: bottom-left(0, 0), top-right(10, 8),
rec2: bottom-left(2, 3), top-right(7, 9)
Output: (2, 3) (7, 8) (2, 8) (7, 3)
Input:
rec1: bottom-left(0, 0), top-right(3, 3),
rec2: bottom-left(1, 1), top-right(2, 2)
Output: (1, 1) (2, 2) (1, 2) (2, 1)

Approach :
As two given points are diagonals of a rectangle. so, x1 < x2, y1 < y2. similarly x3 < x4, y3 < y4.
so, bottom-left and top-right points of intersection rectangle can be found by using formula.

x5 = max(x1, x3);
y5 = max(y1, y3);
x6 = min(x2, x4);
y6 = min(y2, y4);

In case of no intersection, x5 and y5 will always exceed x6 and y5 respectively. The other two points of the rectangle can be found by using simple geometry.
Below is the implementation of the above approach:

C++

// CPP program to find intersection
// rectangle of given two rectangles.
#include <bits/stdc++.h>
using namespace std;
 
// function to find intersection rectangle of given two rectangles.
void FindPoints(int x1, int y1, int x2, int y2,
                int x3, int y3, int x4, int y4)
{
    // gives bottom-left point
    // of intersection rectangle
    int x5 = max(x1, x3);
    int y5 = max(y1, y3);
 
    // gives top-right point
    // of intersection rectangle
    int x6 = min(x2, x4);
    int y6 = min(y2, y4);
 
    // no intersection
    if (x5 > x6 || y5 > y6) {
        cout << "No intersection";
        return;
    }
 
    cout << "(" << x5 << ", " << y5 << ") ";
 
    cout << "(" << x6 << ", " << y6 << ") ";
 
    // gives top-left point
    // of intersection rectangle
    int x7 = x5;
    int y7 = y6;
 
    cout << "(" << x7 << ", " << y7 << ") ";
 
    // gives bottom-right point
    // of intersection rectangle
    int x8 = x6;
    int y8 = y5;
 
    cout << "(" << x8 << ", " << y8 << ") ";
}
 
// Driver code
int main()
{
    // bottom-left and top-right
    // corners of first rectangle
    int x1 = 0, y1 = 0, x2 = 10, y2 = 8;
 
    // bottom-left and top-right
    // corners of first rectangle
    int x3 = 2, y3 = 3, x4 = 7, y4 = 9;
 
    // function call
    FindPoints(x1, y1, x2, y2, x3, y3, x4, y4);
 
    return 0;
}

Java

// Java program to find intersection
// rectangle of given two rectangles.
class GFG
{
 
// function to find intersection
// rectangle of given two rectangles.
static void FindPoints(int x1, int y1,
                       int x2, int y2,
                       int x3, int y3,
                       int x4, int y4)
{
    // gives bottom-left point
    // of intersection rectangle
    int x5 = Math.max(x1, x3);
    int y5 = Math.max(y1, y3);
 
    // gives top-right point
    // of intersection rectangle
    int x6 = Math.min(x2, x4);
    int y6 = Math.min(y2, y4);
 
    // no intersection
    if (x5 > x6 || y5 > y6)
    {
        System.out.println("No intersection");
        return;
    }
 
    System.out.print("(" + x5 + ", " +
                           y5 + ") ");
 
    System.out.print("(" + x6 + ", " +
                           y6 + ") ");
 
    // gives top-left point
    // of intersection rectangle
    int x7 = x5;
    int y7 = y6;
 
    System.out.print("(" + x7 + ", " +
                           y7 + ") ");
 
    // gives bottom-right point
    // of intersection rectangle
    int x8 = x6;
    int y8 = y5;
 
    System.out.print("(" + x8 + ", " +
                           y8 + ") ");
}
 
// Driver code
public static void main(String args[])
{
    // bottom-left and top-right
    // corners of first rectangle
    int x1 = 0, y1 = 0,
        x2 = 10, y2 = 8;
 
    // bottom-left and top-right
    // corners of first rectangle
    int x3 = 2, y3 = 3,
        x4 = 7, y4 = 9;
 
    // function call
    FindPoints(x1, y1, x2, y2,
               x3, y3, x4, y4);
}
}
 
// This code is contributed
// by Arnab Kundu

Python3

# Python 3 program to find intersection
# rectangle of given two rectangles.
 
# function to find intersection
# rectangle of given two rectangles.
def FindPoints(x1, y1, x2, y2,
               x3, y3, x4, y4):
 
    # gives bottom-left point
    # of intersection rectangle
    x5 = max(x1, x3)
    y5 = max(y1, y3)
 
    # gives top-right point
    # of intersection rectangle
    x6 = min(x2, x4)
    y6 = min(y2, y4)
 
    # no intersection
    if (x5 > x6 or y5 > y6) :
        print("No intersection")
        return
 
    print( "(", x5, ", ", y5, ") ", end = " ")
 
    print( "(", x6, ", ", y6, ") ", end = " ")
 
    # gives top-left point
    # of intersection rectangle
    x7 = x5
    y7 = y6
 
    print( "(", x7, ", ", y7, ") ", end = " ")
 
    # gives bottom-right point
    # of intersection rectangle
    x8 = x6
    y8 = y5
 
    print( "(", x8, ", ", y8, ") ")
 
# Driver code
if __name__ == "__main__":
     
    # bottom-left and top-right
    # corners of first rectangle
    x1 = 0
    y1 = 0
    x2 = 10
    y2 = 8
 
    # bottom-left and top-right
    # corners of first rectangle
    x3 = 2
    y3 = 3
    x4 = 7
    y4 = 9
 
    # function call
    FindPoints(x1, y1, x2, y2, x3, y3, x4, y4)
 
# This code is contributed
# by ChitraNayal

C#

// C# program to find intersection
// rectangle of given two rectangles.
using System;
 
class GFG
{
 
// function to find intersection
// rectangle of given two rectangles.
static void FindPoints(int x1, int y1,
                       int x2, int y2,
                       int x3, int y3,
                       int x4, int y4)
{
    // gives bottom-left point
    // of intersection rectangle
    int x5 = Math.Max(x1, x3);
    int y5 = Math.Max(y1, y3);
 
    // gives top-right point
    // of intersection rectangle
    int x6 = Math.Min(x2, x4);
    int y6 = Math.Min(y2, y4);
 
    // no intersection
    if (x5 > x6 || y5 > y6)
    {
        Console.WriteLine("No intersection");
        return;
    }
 
    Console.Write("(" + x5 + ", " +
                        y5 + ") ");
 
    Console.Write("(" + x6 + ", " +
                        y6 + ") ");
 
    // gives top-left point
    // of intersection rectangle
    int x7 = x5;
    int y7 = y6;
 
    Console.Write("(" + x7 + ", " +
                        y7 + ") ");
 
    // gives bottom-right point
    // of intersection rectangle
    int x8 = x6;
    int y8 = y5;
 
    Console.Write("(" + x8 + ", " +
                        y8 + ") ");
}
 
// Driver code
public static void Main()
{
    // bottom-left and top-right
    // corners of first rectangle
    int x1 = 0, y1 = 0,
        x2 = 10, y2 = 8;
 
    // bottom-left and top-right
    // corners of first rectangle
    int x3 = 2, y3 = 3,
        x4 = 7, y4 = 9;
 
    // function call
    FindPoints(x1, y1, x2, y2,
               x3, y3, x4, y4);
}
}
 
// This code is contributed
// by Akanksha Rai

PHP

<?php
// PHP program to find intersection
// rectangle of given two rectangles.
 
// function to find intersection rectangle
// of given two rectangles.
function FindPoints($x1, $y1, $x2, $y2,
                    $x3, $y3, $x4, $y4)
{
    // gives bottom-left point
    // of intersection rectangle
    $x5 = max($x1, $x3);
    $y5 = max($y1, $y3);
 
    // gives top-right point
    // of intersection rectangle
    $x6 = min($x2, $x4);
    $y6 = min($y2, $y4);
 
    // no intersection
    if ($x5 > $x6 || $y5 > $y6)
    {
        echo "No intersection";
        return;
    }
 
    echo "(" . $x5 . ", " . $y5 . ") ";
 
    echo "(" . $x6 . ", " . $y6 . ") ";
 
    // gives top-left point
    // of intersection rectangle
    $x7 = $x5;
    $y7 = $y6;
 
    echo "(" . $x7 . ", " . $y7 . ") ";
 
    // gives bottom-right point
    // of intersection rectangle
    $x8 = $x6;
    $y8 = $y5;
 
    echo "(" . $x8 . ", " . $y8 . ") ";
}
 
// Driver code
 
// bottom-left and top-right
// corners of first rectangle
$x1 = 0; $y1 = 0; $x2 = 10; $y2 = 8;
 
// bottom-left and top-right
// corners of first rectangle
$x3 = 2; $y3 = 3; $x4 = 7; $y4 = 9;
 
// function call
FindPoints($x1, $y1, $x2, $y2,
           $x3, $y3, $x4, $y4);
 
// This code is contributed
// by Akanksha Rai
?>

Javascript

<script>
 
// Javascript program to find intersection
// rectangle of given two rectangles.
 
// Function to find intersection
// rectangle of given two rectangles.
function FindPoints(x1, y1, x2, y2,
                    x3, y3, x4, y4)
{
     
    // Gives bottom-left point
    // of intersection rectangle
    var x5 = Math.max(x1, x3);
    var y5 = Math.max(y1, y3);
 
    // Gives top-right point
    // of intersection rectangle
    var x6 = Math.min(x2, x4);
    var y6 = Math.min(y2, y4);
 
    // No intersection
    if (x5 > x6 || y5 > y6)
    {
        document.write("No intersection");
        return;
    }
    document.write("(" + x5 + ", " +
                         y5 + ") ");
 
    document.write("(" + x6 + ", " +
                         y6 + ") ");
 
    // Gives top-left point
    // of intersection rectangle
    var x7 = x5;
    var y7 = y6;
 
    document.write("(" + x7 + ", " +
                         y7 + ") ");
 
    // Gives bottom-right point
    // of intersection rectangle
    var x8 = x6;
    var y8 = y5;
 
    document.write("(" + x8 + ", " +
                         y8 + ") ");
}
 
// Driver Code
 
// bottom-left and top-right
// corners of first rectangle
var x1 = 0, y1 = 0,
    x2 = 10, y2 = 8;
 
// bottom-left and top-right
// corners of first rectangle
var x3 = 2, y3 = 3,
    x4 = 7, y4 = 9;
 
// Function call
FindPoints(x1, y1, x2, y2,
           x3, y3, x4, y4);
 
// This code is contributed by kirti
 
</script>

Output:

(2, 3) (7, 8) (2, 8) (7, 3)

Time Complexity: O(1)

Attention reader! Don’t stop learning now. Get hold of all the important DSA concepts with the DSA Self Paced Course at a student-friendly price and become industry ready. To complete your preparation from learning a language to DS Algo and many more, please refer Complete Interview Preparation Course.

In case you wish to attend live classes with experts, please refer DSA Live Classes for Working Professionals and Competitive Programming Live for Students.

My Personal Notes