How to find the length of a rectangle whose perimeter and breadth is given?
Last Updated :
21 Dec, 2021
Mensuration entails the processes of measurements and all calculations pertaining to various geometrical shapes, occurring in mathematical theory as well as our daily lives. The study of all geometrical shapes falls under the scope of mensuration. Geometric shapes such as triangles, rectangles, quadrilaterals, circle, etc. Here, rectangle is discussed below,
Rectangle
A rectangle is defined as the type of quadrilateral whose opposite sides are always parallel and equal in length. The adjacent sides intersect each other at right angles. Like all other quadrilaterals, the sum of all the four angles of a rectangle also measures 360°. A rectangle is a 2-D shape, which has only two proportions length and breadth, represented by each pair of its four sides.

The above figure depicts a rectangle ABDC, with AB being parallel to CD and AC being the parallel side to BD. Here, AB and CD represent the length of the rectangle, while AC and BD depict the breadth. The sum of all the four right angles is 360°.
The perimeter of a Rectangle
The perimeter of a 2-D geometrical shape is the sum of lengths of all its sides. So, the perimeter of rectangle ABDC would be:
AB + AC + CD + BD
= l + b + l + b
= 2l + 2b
= 2(l + b).
Hence, the perimeter of a rectangle is twice the sum of its length and breadth.
How to find the length of a rectangle whose perimeter and breadth is given?
Solution:
Let the given perimeter be P units and breadth be x units. Let the length be depicted by l.
Since, Perimeter of a rectangle = 2(l + b)
⇒ P = 2l + 2b
⇒ 2l = P – 2b
⇒ l = 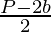
The above formula can be used to find the length of a rectangle whose perimeter and breadth is given.
Similar Problems
Question 1: Find the length of the rectangle whose perimeter is 50 cm and breadth is 10 cm.
Solution:
P = 2(l + b)
Given: P = 50 cm and b = 10 cm
⇒ l = 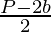
⇒ l = 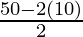
⇒ l = 30/ 2
⇒ l = 15 cm
Question 2: Find the length of the rectangle whose perimeter is 60 cm and breadth is 5 cm.
Solution:
P = 2(l + b)
Given: P = 60 cm and b = 5 cm
⇒ l = 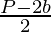
⇒ l = 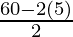
⇒ l = 50/ 2
⇒ l = 25 cm
Question 3: Find the length of the rectangle whose perimeter is 60 cm and breadth is 20 cm.
Solution:
P = 2(l + b)
Given: P = 60 cm and b = 20 cm
⇒ l = 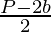
⇒ l = 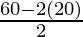
⇒ l = 20/ 2
⇒ l = 10 cm
Question 4: Find the length of the rectangle whose perimeter is 80 cm and breadth is 10 cm.
Solution:
P = 2(l + b)
Given: P = 80 cm and b = 10 cm
⇒ l = 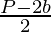
⇒ l = 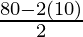
⇒ l = 60/ 2
⇒ l = 30 cm
Question 5: Find the length of the rectangle whose perimeter is 100 cm and breadth is 10 cm.
Solution:
P = 2(l + b)
Given: P = 100 cm and b = 10 cm
⇒ l = 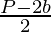
⇒ l = 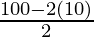
⇒ l = 80/ 2
⇒ l = 40 cm
Question 6: Find the length of the rectangle whose perimeter is 60 cm and breadth is 10 cm.
Solution:
P = 2(l + b)
Given: P = 60 cm and b = 10 cm
⇒ l = 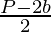
⇒ l = 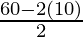
⇒ l = 40/ 2
⇒ l = 20 cm
Share your thoughts in the comments
Please Login to comment...