What is Hashing?
Last Updated :
26 Feb, 2024
Hashing refers to the process of generating a fixed-size output from an input of variable size using the mathematical formulas known as hash functions. This technique determines an index or location for the storage of an item in a data structure.
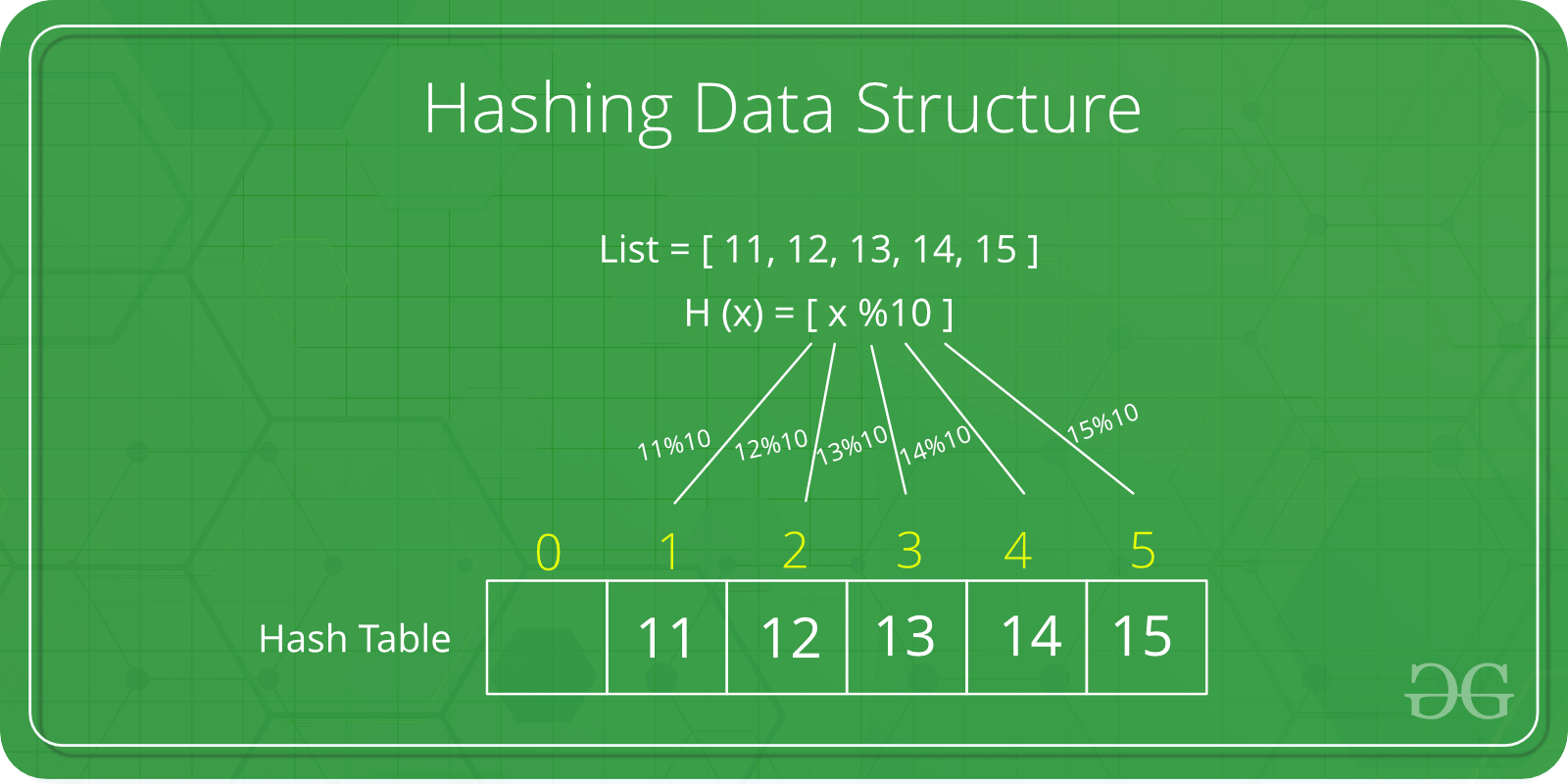
Need for Hash data structure
The amount of data on the internet is growing exponentially every day, making it difficult to store it all effectively. In day-to-day programming, this amount of data might not be that big, but still, it needs to be stored, accessed, and processed easily and efficiently. A very common data structure that is used for such a purpose is the Array data structure.
Now the question arises if Array was already there, what was the need for a new data structure! The answer to this is in the word “efficiency“. Though storing in Array takes O(1) time, searching in it takes at least O(log n) time. This time appears to be small, but for a large data set, it can cause a lot of problems and this, in turn, makes the Array data structure inefficient.
So now we are looking for a data structure that can store the data and search in it in constant time, i.e. in O(1) time. This is how Hashing data structure came into play. With the introduction of the Hash data structure, it is now possible to easily store data in constant time and retrieve them in constant time as well.
Components of Hashing
There are majorly three components of hashing:
- Key: A Key can be anything string or integer which is fed as input in the hash function the technique that determines an index or location for storage of an item in a data structure.
- Hash Function: The hash function receives the input key and returns the index of an element in an array called a hash table. The index is known as the hash index.
- Hash Table: Hash table is a data structure that maps keys to values using a special function called a hash function. Hash stores the data in an associative manner in an array where each data value has its own unique index.

Components of Hashing
What is Collision?
The hashing process generates a small number for a big key, so there is a possibility that two keys could produce the same value. The situation where the newly inserted key maps to an already occupied, and it must be handled using some collision handling technology.

Collision in Hashing
Advantages of Hashing in Data Structures
- Key-value support: Hashing is ideal for implementing key-value data structures.
- Fast data retrieval: Hashing allows for quick access to elements with constant-time complexity.
- Efficiency: Insertion, deletion, and searching operations are highly efficient.
- Memory usage reduction: Hashing requires less memory as it allocates a fixed space for storing elements.
- Scalability: Hashing performs well with large data sets, maintaining constant access time.
- Security and encryption: Hashing is essential for secure data storage and integrity verification.
To learn more about Hashing Please refer to the Introduction to Hashing – Data Structure and Algorithm Tutorials
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...