Hardy’s Rule

Hardy’s Rule is an extension of Newton–Cotes formulas. Consider a function, f(x), tabulated at points 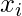equally spaced by 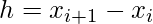such that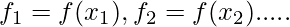 
Given the following inputs 
1. A function 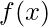, whose integrand has to be computed. 
2. The upper and lower limits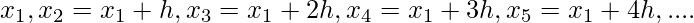 

Hardy’s rule can be derived by approximating the integrand f(x) 

Example : 
The task is to find the integrand of the function using Hardy’s Rule

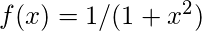upper limit, b = 6,

lower limit a = 0 .

Approach :
Hardy’s Rule is a numerical integration technique to find the approximate value of the integral. 

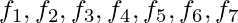are the values of f(x) at their respective intervals of x. 
In order to integrate any function f(x) in the interval (a, b), follow the steps given below:
1.the value of n=6, which is the number of parts the interval is divided into. 
2.Calculate the width, h = (b-a)/6 
3.Calculate the values of x0 to x6 as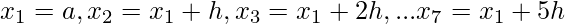 
Consider y = f(x). Now find the values of 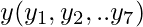for the corresponding 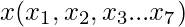values. 
4. Substitute all the above-found values in the Hardy’s rule to calculate the integral value.
Below is the implementation of the above approach: 

C

// C program to implement Hardy's Rule
// on the given function

#include <math.h>
#include <stdio.h>

// In order to represent the implementation,
// a function f(x) = 1/(1 + x) is considered
// in this program

// Function to return the value of f(x)
// for the given value of x
float y(float x)
{
    return (1 / (1 + x));
}

// Function to computes the integrand of y
// at the given intervals of x with
// step size h and the initial limit a
// and final limit b
float Hardyrule(float a, float b)
{
    // Number of intervals

    int n = 6;
    int h;

    // Computing the step size
    h = ((b - a) / n);
    float sum = 0;

    // Substituting a = 0, b = 4 and h = 1
    float hl = (28* y(a) + 162 * y(a + h)

                + 220 * y(a + 3 * h)
                +  162* y(a + 5 * h)
                +28* y(a + 6*h))*h/100
                ;

    sum = sum + hl;
    return sum;
}

// Driver code
int main()
{
    float lowlimit = 0;
    float upplimit = 6;
    printf("f(x) = %.4f",
           Hardyrule(0, 6));
    return 0;
}

Output:

f(x) = 1.9500