Greatest Integer Function
Last Updated :
05 Apr, 2024
The greatest Integer Function [X] indicates an integral part of the real number  which is the nearest and smaller integer to
which is the nearest and smaller integer to  . It is also known as the floor of X.
. It is also known as the floor of X.
[x]=the largest integer that is less than or equal to x.
In general: If,  <=
<=  <
<  . Then,
. Then, ![Rendered by QuickLaTeX.com (n \epsilon Integer)\Longrightarrow [X]=n](https://quicklatex.com/cache3/4b/ql_5e0670e0ade68146e8ac8baffbd0ec4b_l3.png)
This means if X lies in [n, n+1), then the Greatest Integer Function of X will be n.

In the above figure, we are taking the floor of the values each time. When the intervals are in the form of [n, n+1), the value of the greatest integer function is n, where n is an integer.
- 0<=x<1 will always lie in the interval [0, 0.9), so here the Greatest Integer Function of X will be 0.
- 1<=x<2 will always lie in the interval [1, 1.9), so here the Greatest Integer Function of X will be 1.
- 2<=x<3 will always lie in the interval [2, 2.9), so here the Greatest Integer Function of X will be 2.
Examples:
Input: X = 2.3
Output: [2.3] = 2
Input: X = -8.0725
Output: [-8.0725] = -9
Input: X = 2
Output: [2] = 2
Number Line Representation
- If we examine a number line with the integers and plot 2.7 on it, we see:
- The largest integer that is less than 2.7 is 2. So [2.7] = 2.
- If we examine a number line with the integers and plot -1.3 on it, we see:

Since the largest integer that is less than -1.3 is -2, so [-1.3] = 2.
Here, f(x)=[X] could be expressed graphically as:
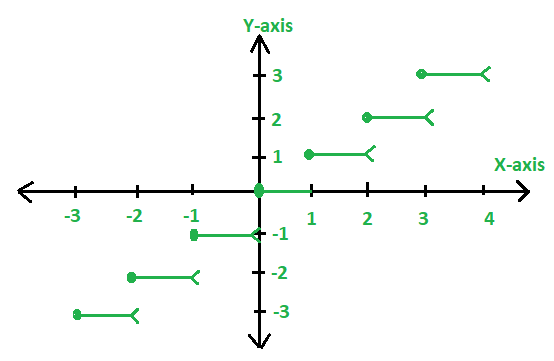
Note: In the above graph, the left endpoint at every step is blocked(dark dot) to show that the point is a member of the graph, and the other right endpoint (open circle) indicates the points that are not part of the graph.
Properties of Greatest Integer Function:
- [X]=X holds if X is an integer.
- [X+I]=[X]+I, if I is an integer, then we can I separately in the Greatest Integer Function.
- [X+Y]>=[X]+[Y], means the greatest integer of the sum of X and Y is the equal sum of the GIF of X and the GIF of Y.
- If [f(X)]>=I, then f(X) >= I.
- If [f(X)]<=I, then f(X) < I+1.
- [-X]= -[X], If X
 Integer.
Integer. - [-X]=-[X]-1, If X is not an Integer.
It is also known as the stepwise function or floor of X.
The below program shows the implementation of the Greatest Integer Function using floor() method.
C++
// CPP program to illustrate
// greatest integer Function
#include <bits/stdc++.h>
using namespace std;
// Function to calculate the
// GIF value of a number
int GIF(float n)
{
// GIF is the floor of a number
return floor(n);
}
// Driver code
int main()
{
int n = 2.3;
cout << GIF(n);
return 0;
}
// Java program to illustrate
// greatest integer Function
class GFG{
// Function to calculate the
// GIF value of a number
static int GIF(double n)
{
// GIF is the floor of a number
return (int)Math.floor(n);
}
// Driver code
public static void main(String[] args)
{
double n = 2.3;
System.out.println(GIF(n));
}
}
// This code is contributed by mits
# Python3 program to illustrate
# greatest integer Function
import math
# Function to calculate the
# GIF value of a number
def GIF(n):
# GIF is the floor of a number
return int(math.floor(n));
# Driver code
n = 2.3;
print(GIF(n));
# This code is contributed by mits
// C# program to illustrate
// greatest integer Function
using System;
class GFG{
// Function to calculate the
// GIF value of a number
static int GIF(double n)
{
// GIF is the floor of a number
return (int)Math.Floor(n);
}
// Driver code
static void Main()
{
double n = 2.3;
Console.WriteLine(GIF(n));
}
}
// This code is contributed by mits
<script>
// Javascript program to illustrate
// greatest integer Function
// Function to calculate the
// GIF value of a number
function GIF(n)
{
// GIF is the floor of a number
return Math.floor(n);
}
// Driver code
var n = 2.3;
document.write(GIF(n));
// This code is contributed by Ankita saini
</script>
<?php
// PHP program to illustrate
// greatest integer Function
// Function to calculate the
// GIF value of a number
function GIF($n)
{
// GIF is the floor of a number
return floor($n);
}
// Driver code
$n = 2.3;
echo GIF($n);
?>
Time Complexity: O(1)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...