Gomory-Hu Tree | Set 1 (Introduction)
Last Updated :
10 Feb, 2018
Background :
In a flow network, an s-t cut is a cut that requires the source ‘s’ and the sink ‘t’ to be in different subsets, and it consists of edges going from the source’s side to the sink’s side. The capacity of an s-t cut is defined by the sum of capacity of each edge in the cut-set. (Source: Wiki). Given a two vertices, s and t, we can find minimum s-t cut using max flow algorithm.
Since there are total O(n2) possible pairs, at first look it seems that there would be total O(n2) total minimum s-t cut values. But when we use Gomory-Hu Tree, we would see that there are total n-1 different cut values [A Tree with n vertices has n-1 edges]
Popular graph problems that can be solved using Gomory-Hu Tree :
- Given a weighted and connected graph, find minimum s-t cut for all pairs of vertices. Or a problem like find minimum of all possible minimum s-t cuts.
- Minimum K-Cut problem : Find minimum weight set of edges whose removal would partition the graph to k connected components. This is a NP-Hard problem, Gomory-Hu Tree provides an approximate solution for this problem.
What is Gomory-Hu Tree?
A Gomory-Hu Tree is defined for a flow graph with edge capacity function c. The tree has same set of vertices as input graph and has n-1 (n is number of vertices) edges. Edge capacity function c’ is defined using following properties:
Equivalent flow tree : For any pair of vertices s and t, the minimum s-t cut in graph is equal to the smallest capacity of the edges on the path between s and t in Tree.
Cut property : a minimum s-t cut in Tree is also a minimum cut in Graph.G
For example, consider the following Graph and Corresponding Gomory-Hu Tree.
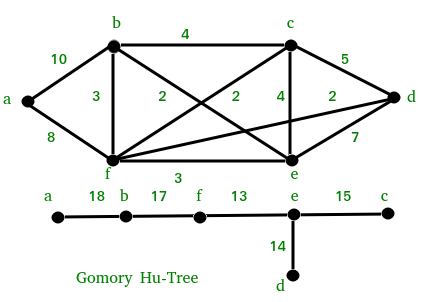
Since there are n-1 edges in a tree with n nodes, we can conclude that there are at most n-1 different flow values in a flow network with n vertices.
We will be discussing construction of Tree in next post.
How to solve above problems using Gomory-Hu Tree is constructed?
The minimum weight edge in the tree is minimum of all s-t cuts.
We can solve the k-cut problem using below steps.
1) Construct Gomory-Hu Tree.
2) Remove k-1 minimum weight (or lightest) edges from the Tree.
3) Return union of components obtained by above removal of edges.
Below diagram illustrates above algorithm.
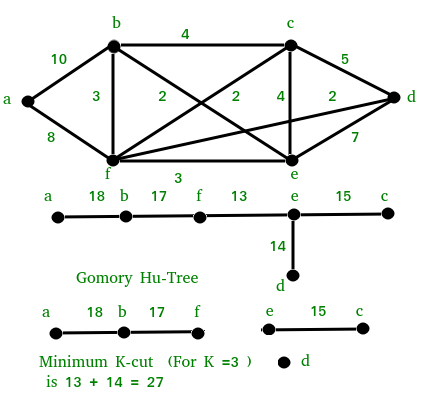
Note that the above solution may not always produce optimal result, but it is guaranteed to produce results within bounds of (2-2/k).
References:
https://www.corelab.ntua.gr/seminar/material/2008-2009/2008.10.20.Gomory-Hu%20trees%20and%20applications.slides.pdf
https://courses.engr.illinois.edu/cs598csc/sp2009/lectures/lecture_7.pdf
https://cseweb.ucsd.edu/classes/fa06/cse202/Gomory-Hu%20Tree.pdf
Share your thoughts in the comments
Please Login to comment...