Full Binary Tree
Last Updated :
02 Jan, 2023
What is a Binary Tree?
A binary tree is a tree data structure with a maximum of 2 children per node. We commonly refer to them as the left and right child as each element in a binary tree may only have two children.
What is a Full Binary Tree?
A full binary tree is a binary tree with either zero or two child nodes for each node.
A full binary tree, on the other hand, does not have any nodes that have only one child node.
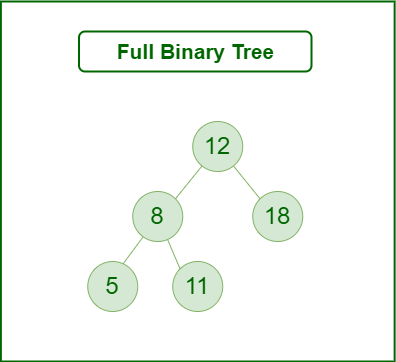
Full Binary Tree
Full Binary Tree Theorem:
Let T be a nonempty, full binary tree Then:
- If T has I internal nodes, the number of leaves is L = I + 1.
This is known as the full binary tree theorem.
Facts derived from the theorem:
- If T has I internal nodes, the total number of nodes is N = 2I + 1.
- If T has a total of N nodes, the number of internal nodes is I = (N – 1)/2.
- If T has a total of N nodes, the number of leaves is L = (N + 1)/2.
- If T has L leaves, the total number of nodes is N = 2L – 1.
- If T has L leaves, the number of internal nodes is I = L – 1.
Some other properties:
- There are a maximum of 2k nodes in level k for every k >= 0.
- The binary tree with λ levels has maximum of 2λ-1 nodes.
- The binary tree with N nodes has the number of levels at least [log (N + 1)].
- The binary tree with L leaves has the number of leaves at least [log L] + 1.
Related Articles:
Share your thoughts in the comments
Please Login to comment...