First digit in product of an array of numbers

Given an array of ‘n’ numbers. We need to find the first digit of product of these ‘n’ numbers 
Examples :

Input  : arr[] = {5, 8, 3, 7}
Output : 8
        Product of 5, 8, 3, 7 is 840
        and its first  digit is 8

Input  : arr[] = {6, 7, 9}
Output : 3

Background : 
First we start from a very basic question how to find the first digit of any number x.To do this keep dividing the number until it is greater than equal to 10. After doing this the number which we will get will be first digit of x 

C++

// C++ implementation to find first digit of a
// single number
#include <bits/stdc++.h>
using namespace std;

int firstDigit(int x)
{
    // Keep dividing by 10 until it is
    // greater than equal to 10
    while (x >= 10)
        x = x / 10;
    return x;
}

// driver function
int main()
{
    cout << firstDigit(12345) << endl;
    cout << firstDigit(5432) << endl;
}

Java

// Java implementation to find first digit of a
// single number

class Test {
    static int firstDigit(int x)
    {
        // Keep dividing by 10 until it is
        // greater than equal to 10
        while (x >= 10)
            x = x / 10;
        return x;
    }

    // Driver method
    public static void main(String args[])
    {
        System.out.println(firstDigit(12345));
        System.out.println(firstDigit(5432));
    }
}

Python3

# Python implementation to
# find first digit of a
# single number

def firstDigit(x):

    # Keep dividing by 10 until it is
    # greater than equal to 10
    while(x >= 10):
        x = x//10
    return x


# driver function

print(firstDigit(12345))
print(firstDigit(5432))

# This code is contributed
# by Anant Agarwal.

C#

// C# implementation to find first
// digit of a single number
using System;

public class GFG {

    static int firstDigit(int x)
    {

        // Keep dividing by 10 until
        // it is greater than equal
        // to 10
        while (x >= 10)
            x = x / 10;

        return x;
    }

    // Driver method
    public static void Main()
    {
        Console.WriteLine(
                  firstDigit(12345));

        Console.WriteLine(
                   firstDigit(5432));
    }
}

// This code is contributed by Sam007.

PHP

<?php
// PHP implementation to
// find first digit of a
// single number

function firstDigit($x)
{

    // Keep dividing by 10
    // until it is greater
    // than equal to 10
    while ($x >= 10)
        $x = $x / 10;
    return floor($x);
}

    // Driver Code
    echo firstDigit(12345),"\n" ;
    echo firstDigit(5432) ;

// This code is contributed by vishal tripathi.
?>

Javascript

<script>

// Javascript implementation to
// find first digit of a
// single number

function firstDigit(x)
{

    // Keep dividing by 10
    // until it is greater
    // than equal to 10
    while (x >= 10)
        x = x / 10;
    return Math.floor(x);
}

    // Driver Code
    document.write( firstDigit(12345)+"<br>" );
    document.write( firstDigit(5432)) ;

// This code is contributed by Bobby

</script>

Output: 

1
5

Solution :
For an array of numbers, product can be very big and their multiplication might not fit in any typical data type. Even if you use Big int the number will very big and finding the first by direct division by 10 method will be very slow. So we need to use something different 
let the numbers be 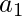, , 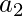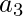……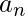and their product is P .P = *…..*. 
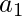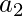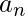let S = 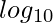(P) = () + ()…..+().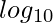 
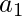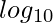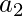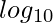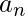So we can say P = .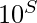 
We know that any number can be written as sum of its floor value and fractional value. 
therefore P = 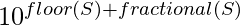which implies P = *. 
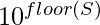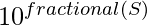Now we can apply our above discussed method of finding first digit of a number because after dividing P by 10 until it is greater than equal to 10 we will be left only with 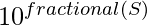which will be our answer. And fractional(S) can be easily calculated fractional(S) = S – floor(S). 

C++

// C++ implementation of finding first digit
// of product of n numbers
#include <bits/stdc++.h>
using namespace std;

// returns the first digit of product of elements of arr[]
int FirstDigit(int arr[], int n)
{
    // stores the logarithm of product of elements of arr[]
    double S = 0;
    for (int i = 0; i < n; i++)
        S = S + log10(arr[i] * 1.0);

    // fractional(s) = s - floor(s)
    double fract_S = S - floor(S);

    // ans = 10^fract_s
    int ans = pow(10, fract_S);
    return ans;
}

// Driver function
int main()
{
    int arr[] = { 5, 8, 3, 7 };
    int n = sizeof(arr) / sizeof(arr[0]);
    cout << FirstDigit(arr, n) << endl;
    return 0;
}

Java

// Java implementation of finding first digit
// of product of n numbers

class Test {
    // returns the first digit of product of elements of arr[]
    static int FirstDigit(int arr[], int n)
    {
        // stores the logarithm of product of elements of arr[]
        double S = 0;
        for (int i = 0; i < n; i++)
            S = S + Math.log10(arr[i] * 1.0);

        // fractional(s) = s - floor(s)
        double fract_S = S - Math.floor(S);

        // ans = 10^fract_s
        int ans = (int)Math.pow(10, fract_S);
        return ans;
    }

    // Driver method
    public static void main(String args[])
    {
        int arr[] = { 5, 8, 3, 7 };

        System.out.println(FirstDigit(arr, arr.length));
    }
}

Python3

# Python implementation of
# finding first digit
# of product of n numbers

import math

# Returns the first digit of
# product of elements of arr[]
def FirstDigit (arr, n):

    # stores the logarithm of
    # product of elements of arr[]
    S = 0
    for i in range(n):
        S = S + math.log10(arr[i]*1.0)

    # fractional(s) = s - floor(s)
    fract_S = S - math.floor(S)

    # ans = 10 ^ fract_s
    ans = math.pow(10, fract_S)
    return ans

# Driver function

arr = [5, 8, 3, 7]
n = len(arr)
print((int)(FirstDigit(arr, n)))

# This code is contributed
# by Anant Agarwal.

C#

// C# implementation of finding first
// digit of product of n numbers
using System;

public class GFG {

    // returns the first digit of product
    // of elements of arr[]
    static int FirstDigit(int[] arr, int n)
    {

        // stores the logarithm of product
        // of elements of arr[]
        double S = 0;

        for (int i = 0; i < n; i++)
            S = S + Math.Log10(arr[i] * 1.0);

        // fractional(s) = s - floor(s)
        double fract_S = S - Math.Floor(S);

        // ans = 10^fract_s
        int ans = (int)Math.Pow(10, fract_S);

        return ans;
    }

    // Driver method
    public static void Main()
    {
        int[] arr = { 5, 8, 3, 7 };
        int n = arr.Length;

        Console.WriteLine(FirstDigit(arr, n));
    }
}

// This code is contributed by Sam007.

PHP

<?php
// PHP implementation of
// finding first digit of
// product of n numbers

// Returns the first digit of
// product of elements of arr[]
function FirstDigit($arr, $n)
{
    // stores the logarithm of
    // product of elements of arr[]
    $S = 0;
    for ($i = 0; $i < $n; $i++)
        $S = $S + log10($arr[$i] * 1.0);

    // fractional(s) = s - floor(s)
    $fract_S = $S - floor($S);

    // ans = 10^fract_s
    $ans = pow(10, $fract_S);
    return floor($ans);
}

// Driver Code
$arr = array ( 5, 8, 3, 7 );
$n = sizeof($arr);
echo FirstDigit($arr, $n);

// This code is contributed by aj_36
?>

Javascript

<script>
    // Javascript implementation of finding first
    // digit of product of n numbers

    // returns the first digit of product
    // of elements of arr[]
    function FirstDigit(arr, n)
    {

        // stores the logarithm of product
        // of elements of arr[]
        let S = 0;

        for (let i = 0; i < n; i++)
            S = S + Math.log10(arr[i] * 1.0);

        // fractional(s) = s - floor(s)
        let fract_S = S - Math.floor(S);

        // ans = 10^fract_s
        let ans = parseInt(Math.pow(10, fract_S), 10);

        return ans;
    }

    let arr = [ 5, 8, 3, 7 ];
    let n = arr.length;

    document.write(FirstDigit(arr, n));

</script>

Output :

8

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.