Finding sum of digits of a number until sum becomes single digit
Last Updated :
13 Jun, 2022
Given a number n, we need to find the sum of its digits such that:
If n < 10
digSum(n) = n
Else
digSum(n) = Sum(digSum(n))
Examples :
Input : 1234
Output : 1
Explanation : The sum of 1+2+3+4 = 10,
digSum(x) == 10
Hence ans will be 1+0 = 1
Input : 5674
Output : 4
A brute force approach is to sum all the digits until the sum < 10.
Flowchart:
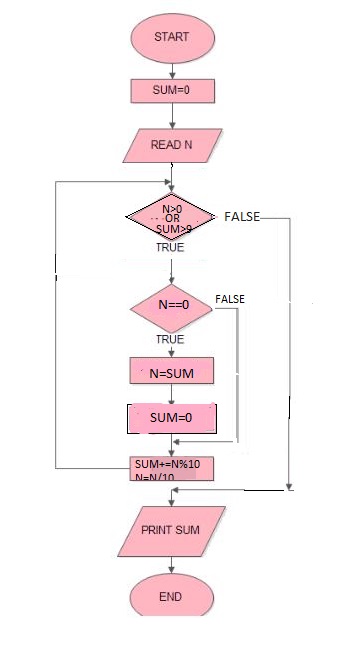
Below is the brute force program to find the sum.
C++
#include<bits/stdc++.h>
using namespace std;
int digSum(int n)
{
int sum = 0;
while(n > 0 || sum > 9)
{
if(n == 0)
{
n = sum;
sum = 0;
}
sum += n % 10;
n /= 10;
}
return sum;
}
int main()
{
int n = 1234;
cout << digSum(n);
return 0;
}
|
Java
import java.util.*;
public class GfG {
static int digSum(int n)
{
int sum = 0;
while (n > 0 || sum > 9)
{
if (n == 0) {
n = sum;
sum = 0;
}
sum += n % 10;
n /= 10;
}
return sum;
}
public static void main(String argc[])
{
int n = 1234;
System.out.println(digSum(n));
}
}
|
Python
import math
def digSum( n):
sum = 0
while(n > 0 or sum > 9):
if(n == 0):
n = sum
sum = 0
sum += n % 10
n /= 10
return sum
n = 1234
print (digSum(n))
|
C#
using System;
class GFG {
static int digSum(int n)
{
int sum = 0;
while (n > 0 || sum > 9)
{
if (n == 0)
{
n = sum;
sum = 0;
}
sum += n % 10;
n /= 10;
}
return sum;
}
public static void Main()
{
int n = 1234;
Console.Write(digSum(n));
}
}
|
PHP
<?php
function digSum( $n)
{
$sum = 0;
while($n > 0 || $sum > 9)
{
if($n == 0)
{
$n = $sum;
$sum = 0;
}
$sum += $n % 10;
$n = (int)$n / 10;
}
return $sum;
}
$n = 1234;
echo digSum($n);
?>
|
Javascript
<script>
let n = 1234;
function getSum(n) {
let sum = 0;
while (n > 0 || sum > 9) {
if(n == 0) {
n = sum;
sum = 0;
}
sum = sum + n % 10;
n = Math.floor(n / 10);
}
return sum;
}
document.write(getSum(n));
</script>
|
C
#include<stdio.h>
int digSum(int n)
{
int sum = 0;
while(n > 0 || sum > 9)
{
if(n == 0)
{
n = sum;
sum = 0;
}
sum += n % 10;
n /= 10;
}
return sum;
}
int main()
{
int n = 1234;
printf("%d",digSum(n));
return 0;
}
|
Output :
1
Time Complexity: O(log(n)).
Auxiliary Space: O(1)
So, another challenge is “Could you do it without any loop/recursion in O(1) runtime?”
YES!!
There exists a simple and elegant O(1) solution for this too. The answer is given simply:-
If n == 0
return 0;
If n % 9 == 0
digSum(n) = 9
Else
digSum(n) = n % 9
How does the above logic works?
The logic behind this approach is :
To check if a number is divisible by 9, add the digits of the number and check if the sum is divisible by 9 or not. If yes, is the case, the number is divisible by 9, otherwise, it’s not.
let’s take 27 i.e (2+7 = 9) hence divisible by 9.
If a number n is divisible by 9, then the sum of its digit until the sum becomes a single digit is always 9. For example,
Let, n = 2880
Sum of digits = 2 + 8 + 8 = 18: 18 = 1 + 8 = 9
Therefore,
A number can be of the form 9x or 9x + k. For the first case, the answer is always 9. For the second case, and is always k which is the remainder left.
The problem is widely known as the digit root problem.
You may find this Wikipedia article useful. -> https://en.wikipedia.org/wiki/Digital_root
Below is the implementation of the above idea :
C++
#include<bits/stdc++.h>
using namespace std;
int digSum(int n)
{
if (n == 0)
return 0;
return (n % 9 == 0) ? 9 : (n % 9);
}
int main()
{
int n = 9999;
cout<<digSum(n);
return 0;
}
|
Java
import java.io.*;
class GFG {
static int digSum(int n)
{
if (n == 0)
return 0;
return (n % 9 == 0) ? 9 : (n % 9);
}
public static void main (String[] args)
{
int n = 9999;
System.out.println(digSum(n));
}
}
|
Python3
def digSum(n):
if (n == 0):
return 0
if (n % 9 == 0):
return 9
else:
return (n % 9)
n = 9999
print(digSum(n))
|
C#
using System;
class GFG
{
static int digSum(int n)
{
if (n == 0)
return 0;
return (n % 9 == 0) ? 9 : (n % 9);
}
public static void Main ()
{
int n = 9999;
Console.Write(digSum(n));
}
}
|
PHP
<?php
function digSum($n)
{
if ($n == 0)
return 0;
return ($n % 9 == 0) ? 9 : ($n % 9);
}
$n = 9999;
echo digSum($n);
?>
|
Javascript
<script>
function digSum(n)
{
if (n == 0)
return 0;
return (n % 9 == 0) ? 9 : (n % 9);
}
n = 9999;
document.write(digSum(n));
</script>
|
Output:
9
Time Complexity: O(1)
Auxiliary Space: O(1)
Related Post :
https://www.geeksforgeeks.org/digital-rootrepeated-digital-sum-given-integer/
Share your thoughts in the comments
Please Login to comment...