Find the position of the last removed element from the array
Last Updated :
08 Sep, 2022
Given an array of size 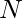 and an integer
and an integer 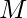 . Perform the following operations on the given array:
. Perform the following operations on the given array:
- If a[i] > M then push a[i] – M to end of the array, otherwise remove it from the array.
- Perform the first operation while the array is non-empty.
The task is to find the original position of the element which gets removed last.
Examples:
Input: arr[] = {4, 3}, M = 2
Output: 2
Remove 4 from the array and the array becomes {3, 2} with original positions {2, 1}
Remove 3 from the array and the array becomes {2, 1} with original positions {1, 2}
Remove 2 from the array and the array becomes {1} with original positions {2}
So, 2nd positioned element is the last to be removed from the array.
Input: arr[] = {2, 5, 4}, M = 2
Output: 2
The idea is to observe the last element which will be removed from the array. It can by easily said that the element to be removed last will be the element which can be subtracted max number of times by 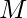 among all elements of the array. That is, the element with maximum value of ceil(a[i] / M).
among all elements of the array. That is, the element with maximum value of ceil(a[i] / M).
So, the task now reduces to find the index of the element in the array with maximum value of ceil(a[i] / M).
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int getPosition(int a[], int n, int m)
{
for (int i = 0; i < n; i++) {
a[i] = (a[i] / m + (a[i] % m != 0));
}
int ans = -1, max = -1;
for (int i = n - 1; i >= 0; i--) {
if (max < a[i]) {
max = a[i];
ans = i;
}
}
return ans + 1;
}
int main()
{
int a[] = { 2, 5, 4 };
int n = sizeof(a) / sizeof(a[0]);
int m = 2;
cout << getPosition(a, n, m);
return 0;
}
|
Java
import java.util.*;
class solution
{
static int getPosition(int a[], int n, int m)
{
for (int i = 0; i < n; i++) {
a[i] = (a[i] / m + (a[i] % m));
}
int ans = -1, max = -1;
for (int i = n - 1; i >= 0; i--) {
if (max < a[i]) {
max = a[i];
ans = i;
}
}
return ans + 1;
}
public static void main(String args[])
{
int a[] = { 2, 5, 4 };
int n = a.length;
int m = 2;
System.out.println(getPosition(a, n, m));
}
}
|
Python3
import math as mt
def getPosition(a, n, m):
for i in range(n):
a[i] = (a[i] // m +
(a[i] % m != 0))
ans, maxx = -1,-1
for i in range(n - 1, -1, -1):
if (maxx < a[i]):
maxx = a[i]
ans = i
return ans + 1
a = [2, 5, 4]
n = len(a)
m = 2
print(getPosition(a, n, m))
|
C#
using System;
class GFG
{
static int getPosition(int []a,
int n, int m)
{
for (int i = 0; i < n; i++)
{
a[i] = (a[i] / m + (a[i] % m));
}
int ans = -1, max = -1;
for (int i = n - 1; i >= 0; i--)
{
if (max < a[i])
{
max = a[i];
ans = i;
}
}
return ans + 1;
}
static public void Main ()
{
int []a = { 2, 5, 4 };
int n = a.Length;
int m = 2;
Console.WriteLine(getPosition(a, n, m));
}
}
|
PHP
<?php
function getPosition($a, $n, $m)
{
for ( $i = 0; $i < $n; $i++)
{
$a[$i] = ($a[$i] / $m +
($a[$i] % $m != 0));
}
$ans = -1;
$max = -1;
for ($i = $n - 1; $i >= 0; $i--)
{
if ($max < $a[$i])
{
$max = $a[$i];
$ans = $i;
}
}
return $ans + 1;
}
$a = array( 2, 5, 4 );
$n = sizeof($a);
$m = 2;
echo getPosition($a, $n, $m);
?>
|
Javascript
<script>
function getPosition(a, n, m)
{
for(let i = 0; i < n; i++)
{
a[i] = (a[i] / m + (a[i] % m));
}
let ans = -1, max = -1;
for(let i = n - 1; i >= 0; i--)
{
if (max < a[i])
{
max = a[i];
ans = i;
}
}
return ans + 1;
}
let a = [ 2, 5, 4 ];
let n = a.length;
let m = 2;
document.write(getPosition(a, n, m));
</script>
|
Complexity Analysis:
- Time Complexity: O(n)
- Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...