Find the position of the last removed element from the array

Difficulty Level : Easy
Last Updated : 03 May, 2021

Given an array of size 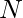$N$ and an integer 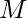$M$ . Perform the following operations on the given array:

If a[i] > M then push a[i] – M to end of the array, otherwise remove it from the array.
Perform the first operation while the array is non-empty.

The task is to find the original position of the element which gets removed last.

Examples:

Input: arr[] = {4, 3}, M = 2
Output: 2
Remove 4 from the array and the array becomes {3, 2} with original positions {2, 1}
Remove 3 from the array and the array becomes {2, 1} with original positions {1, 2}
Remove 2 from the array and the array becomes {1} with original positions {2}
So, 2nd positioned element is the last to be removed from the array.
Input: arr[] = {2, 5, 4}, M = 2
Output: 2

The idea is to observe the last element which will be removed from the array. It can by easily said that the element to be removed last will be the element which can be subtracted max number of times by 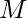$M$ among all elements of the array. That is, the element with maximum value of ceil(a[i] / M).

So, the task now reduces to find the index of the element in the array with maximum value of ceil(a[i] / M).

Below is the implementation of the above approach:

C++

// C++ program to find the position of the
// last removed element from the array
#include <bits/stdc++.h>
using namespace std;
 
// Function to find the original position
// of the element which will be
// removed last
int getPosition(int a[], int n, int m)
{
    // take ceil of every number
    for (int i = 0; i < n; i++) {
        a[i] = (a[i] / m + (a[i] % m != 0));
    }
 
    int ans = -1, max = -1;
    for (int i = n - 1; i >= 0; i--) {
        if (max < a[i]) {
            max = a[i];
            ans = i;
        }
    }
 
    // Since position is index+1
    return ans + 1;
}
 
// Driver code
int main()
{
    int a[] = { 2, 5, 4 };
 
    int n = sizeof(a) / sizeof(a[0]);
 
    int m = 2;
 
    cout << getPosition(a, n, m);
 
    return 0;
}

Java

// Java program to find the position of the
// last removed element from the array
import java.util.*;
 
class solution
{
 
// Function to find the original position
// of the element which will be
// removed last
 
static int getPosition(int a[], int n, int m)
{
    // take ceil of every number
    for (int i = 0; i < n; i++) {
        a[i] = (a[i] / m + (a[i] % m));
    }
 
    int ans = -1, max = -1;
    for (int i = n - 1; i >= 0; i--) {
        if (max < a[i]) {
            max = a[i];
            ans = i;
        }
    }
 
    // Since position is index+1
    return ans + 1;
}
 
// Driver code
public static void main(String args[])
{
    int a[] = { 2, 5, 4 };
 
    int n = a.length;
 
    int m = 2;
 
System.out.println(getPosition(a, n, m));
 
}
 
}
//This code is contributed by
// Surendra_Gangwar

Python3

# Python3 program to find the position of
# the last removed element from the array
import math as mt
 
# Function to find the original
# position of the element which
# will be removed last
def getPosition(a, n, m):
 
    # take ceil of every number
    for i in range(n):
        a[i] = (a[i] // m +
               (a[i] % m != 0))
     
    ans, maxx = -1,-1
    for i in range(n - 1, -1, -1):
        if (maxx < a[i]):
            maxx = a[i]
            ans = i
             
    # Since position is index+1
    return ans + 1
 
# Driver code
a = [2, 5, 4]
 
n = len(a)
 
m = 2
 
print(getPosition(a, n, m))
 
# This is contributed by Mohit kumar 29

C#

// C# program to find the position of the
// last removed element from the array
using System;
 
class GFG
{
     
// Function to find the original
// position of the element which
// will be removed last
static int getPosition(int []a,
                       int n, int m)
{
    // take ceil of every number
    for (int i = 0; i < n; i++)
    {
        a[i] = (a[i] / m + (a[i] % m));
    }
 
    int ans = -1, max = -1;
    for (int i = n - 1; i >= 0; i--)
    {
        if (max < a[i])
        {
            max = a[i];
            ans = i;
        }
    }
 
    // Since position is index+1
    return ans + 1;
}
 
// Driver code
static public void Main ()
{
    int []a = { 2, 5, 4 };
    int n = a.Length;
    int m = 2;
    Console.WriteLine(getPosition(a, n, m));
}
}
 
// This code is contributed by ajit

PHP

<?php
// PHP program to find the position of the
// last removed element from the array
 
// Function to find the original
// position of the element which
// will be removed last
function getPosition($a, $n, $m)
{
    // take ceil of every number
    for ( $i = 0; $i < $n; $i++)
    {
        $a[$i] = ($a[$i] / $m +
                 ($a[$i] % $m != 0));
    }
 
    $ans = -1;
    $max = -1;
    for ($i = $n - 1; $i >= 0; $i--)
    {
        if ($max < $a[$i])
        {
            $max = $a[$i];
            $ans = $i;
        }
    }
 
    // Since position is index+1
    return $ans + 1;
}
 
// Driver code
$a = array( 2, 5, 4 );
$n = sizeof($a);
$m = 2;
 
echo getPosition($a, $n, $m);
 
// This code is contributed by jit_t
?>

Javascript

<script>
 
// Javascript program to find the position
// of the last removed element from the array
 
// Function to find the original
// position of the element which
// will be removed last
function getPosition(a, n, m)
{
     
    // Take ceil of every number
    for(let i = 0; i < n; i++)
    {
        a[i] = (a[i] / m + (a[i] % m));
    }
 
    let ans = -1, max = -1;
    for(let i = n - 1; i >= 0; i--)
    {
        if (max < a[i])
        {
            max = a[i];
            ans = i;
        }
    }
 
    // Since position is index+1
    return ans + 1;
}
 
// Driver code
let a = [ 2, 5, 4 ];
let n = a.length;
let m = 2;
 
document.write(getPosition(a, n, m));
 
// This code is contributed by rameshtravel07
 
</script>

Output:

My Personal Notes

Related Articles

Find the position of the last removed element from the array

C++

Java

Python3

C#

PHP

Javascript