Find the number of distinct pairs of vertices which have a distance of exactly k in a tree
Last Updated :
22 Jun, 2022
Given an integer k and a tree with n nodes. The task is to count the number of distinct pairs of vertices that have a distance of exactly k.
Examples:
Input: k = 2
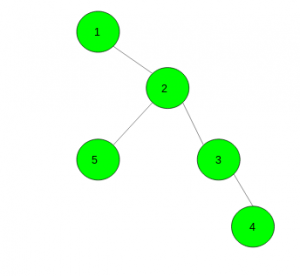
Output: 4
Input: k = 3
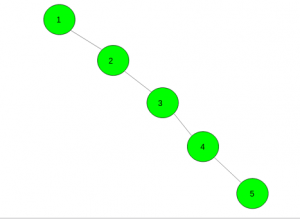
Output: 2
Approach: This problem can be solved using dynamic programming. For every vertex v of the tree, we calculate values d[v][lev] (0 <= lev <= k). This value indicates the number of vertices having distance lev from v. Note that d[v][0] = 1.
Then we calculate the answer. For any vertex v number of pairs will be a product of the number of vertices at level j – 1 and level k – j.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define N 5005
int n, k;
vector<int> gr[N];
int d[N][505];
int ans = 0;
void Add_edge(int x, int y)
{
gr[x].push_back(y);
gr[y].push_back(x);
}
void dfs(int v, int par)
{
d[v][0] = 1;
for (auto i : gr[v]) {
if (i != par) {
dfs(i, v);
for (int j = 1; j <= k; j++)
ans += d[i][j - 1] * d[v][k - j];
for (int j = 1; j <= k; j++)
d[v][j] += d[i][j - 1];
}
}
}
int main()
{
n = 5, k = 2;
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(3, 4);
Add_edge(2, 5);
dfs(1, 0);
cout << ans;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static final int N = 5005;
static int n, k;
static Vector<Integer>[] gr = new Vector[N];
static int[][] d = new int[N][505];
static int ans = 0;
static void Add_edge(int x, int y)
{
gr[x].add(y);
gr[y].add(x);
}
static void dfs(int v, int par)
{
d[v][0] = 1;
for (Integer i : gr[v])
{
if (i != par)
{
dfs(i, v);
for (int j = 1; j <= k; j++)
ans += d[i][j - 1] * d[v][k - j];
for (int j = 1; j <= k; j++)
d[v][j] += d[i][j - 1];
}
}
}
public static void main(String[] args)
{
n = 5;
k = 2;
for (int i = 0; i < N; i++)
gr[i] = new Vector<Integer>();
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(3, 4);
Add_edge(2, 5);
dfs(1, 0);
System.out.print(ans);
}
}
|
Python3
N = 5005
n, k = 0, 0
gr = [[] for i in range(N)]
d = [[0 for i in range(505)]
for i in range(N)]
ans = 0
def Add_edge(x, y):
gr[x].append(y)
gr[y].append(x)
def dfs(v, par):
global ans
d[v][0] = 1
for i in gr[v]:
if (i != par):
dfs(i, v)
for j in range(1, k + 1):
ans += d[i][j - 1] * d[v][k - j]
for j in range(1, k + 1):
d[v][j] += d[i][j - 1]
n = 5
k = 2
Add_edge(1, 2)
Add_edge(2, 3)
Add_edge(3, 4)
Add_edge(2, 5)
dfs(1, 0)
print(ans)
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static readonly int N = 5005;
static int n, k;
static List<int>[] gr = new List<int>[N];
static int[,] d = new int[N, 505];
static int ans = 0;
static void Add_edge(int x, int y)
{
gr[x].Add(y);
gr[y].Add(x);
}
static void dfs(int v, int par)
{
d[v, 0] = 1;
foreach (int i in gr[v])
{
if (i != par)
{
dfs(i, v);
for (int j = 1; j <= k; j++)
ans += d[i, j - 1] * d[v, k - j];
for (int j = 1; j <= k; j++)
d[v, j] += d[i, j - 1];
}
}
}
public static void Main(String[] args)
{
n = 5;
k = 2;
for (int i = 0; i < N; i++)
gr[i] = new List<int>();
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(3, 4);
Add_edge(2, 5);
dfs(1, 0);
Console.Write(ans);
}
}
|
PHP
<?php
$N = 5005;
$gr = array_fill(0, $N, array());
$d = array_fill(0, $N,
array_fill(0, 505, 0));
$ans = 0;
function Add_edge($x, $y)
{
global $gr;
array_push($gr[$x], $y);
array_push($gr[$y], $x);
}
function dfs($v, $par)
{
global $d, $ans, $k, $gr;
$d[$v][0] = 1;
foreach ($gr[$v] as &$i)
{
if ($i != $par)
{
dfs($i, $v);
for ($j = 1; $j <= $k; $j++)
$ans += $d[$i][$j - 1] *
$d[$v][$k - $j];
for ($j = 1; $j <= $k; $j++)
$d[$v][$j] += $d[$i][$j - 1];
}
}
}
$n = 5;
$k = 2;
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(3, 4);
Add_edge(2, 5);
dfs(1, 0);
echo $ans;
?>
|
Javascript
<script>
let N = 5005;
let n, k;
let gr = new Array(N);
let d = new Array(N);
for(let i = 0 ; i < N; i++)
{
d[i] = new Array(505);
for(let j = 0; j < 505; j++)
{
d[i][j] = 0;
}
}
let ans = 0;
function Add_edge(x, y)
{
gr[x].push(y);
gr[y].push(x);
}
function dfs(v, par)
{
d[v][0] = 1;
for(let i = 0; i < gr[v].length; i++)
{
if (gr[v][i] != par)
{
dfs(gr[v][i], v);
for(let j = 1; j <= k; j++)
ans += d[gr[v][i]][j - 1] * d[v][k - j];
for(let j = 1; j <= k; j++)
d[v][j] += d[gr[v][i]][j - 1];
}
}
}
n = 5;
k = 2;
for(let i = 0; i < N; i++)
gr[i] = [];
Add_edge(1, 2);
Add_edge(2, 3);
Add_edge(3, 4);
Add_edge(2, 5);
dfs(1, 0);
document.write(ans);
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(N * 505)
Share your thoughts in the comments
Please Login to comment...