Find min and max values among all maximum leaf nodes from all possible Binary Max Heap
Last Updated :
05 Jul, 2021
Given a positive integer N, the task is to find the largest and smallest elements, from the maximum leaf nodes of every possible binary max-heap formed by taking the first N natural numbers as the nodes’ value of the binary max-heap.
Examples:
Input: N = 2
Output: 1 1
Explanation:
There is only one maximum binary heap with the nodes {1, 2}:
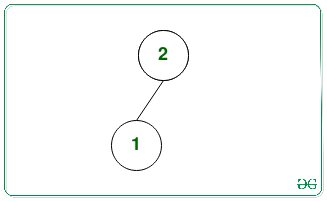
In the above tree, maximum leaf node value = 1.
Therefore, the largest element is 1 and the smallest element is also 1.
Input: N = 3
Output: 2 2
Explanation:
There are two possible maximum binary heaps with the nodes {1, 2, 3}:
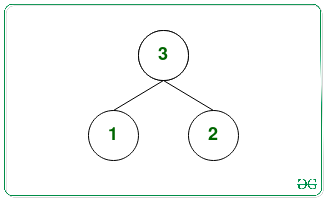
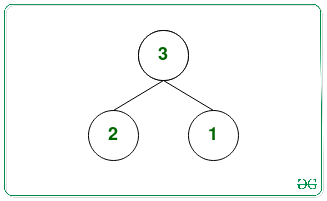
The maximum leaf nodes of first and second heaps are 2 and 2 respectively.
Therefore, the largest element is 2 and the smallest element is also 2.
Naive Approach: The simplest approach is to generate all possible max binary heaps that can be formed from first N natural numbers and keep track of the smallest and largest leaf node values among all the maximum leaf nodes in all the heaps.
Time Complexity: O(N*N!)
Auxiliary Space: O(1)
Efficient Approach: The above approach can be optimized based on the following observations:
- The max heap is a complete binary tree, therefore, the height and count of the number of leaf nodes are fixed.
- In the max heap, the value of the node is always greater than or equal to the children of that node.
- The maximum leaf node value is always greater than or equal to the number of leaves in the tree. Therefore, the maximum value of a leaf node will be minimized if the smallest numbers are placed at the leaf nodes. And will be equal to the number of leaves node.
- One more property of the max heaps is as one will go down the tree the values of nodes decrease. Therefore, the maximum value of a node will be maximized if a number is placed at the leaf node with the least possible depth. So if D is the depth of that node then the maximum possible value of the node will be equal to the N-D.
- If D is the depth of the max Heap then the possible Depths of the leaf nodes are D and D-1 only, as the heaps are the complete binary tree.
- If V is a leaf node then (2*V) must be greater than N. Therefore, the count of leaf nodes is equal to the, (N – N/2).
Follow the steps below to solve the problem:
numberOfleaves = (N- N/2).
D = ceil(log2(N+1))-1
- If N+1 is not a power of 2 and D is greater than 1, then there must exit a leaf node at depth D-1. Therefore, then decrement D by 1.
- Finally, after completing the above steps, print the largest value as (N-D) and the smallest value as numberOfleaves.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void leafNodeValues(int N)
{
int numberOfLeaves = (N - N / 2);
int minDepth = ceil(log2(N + 1)) - 1;
N++;
if (minDepth > 1 && (N & (N - 1)))
minDepth--;
cout << numberOfLeaves << ' '
<< N - minDepth - 1;
}
int main()
{
int N = 2;
leafNodeValues(N);
return 0;
}
|
Java
class GFG{
static void leafNodeValues(int N)
{
int numberOfLeaves = (N - N / 2);
int minDepth = (int)Math.ceil(Math.log(N + 1) /
Math.log(2)) - 1;
N++;
if (minDepth > 1 && (N & (N - 1)) != 0)
minDepth--;
System.out.println(numberOfLeaves + " " +
(N - minDepth - 1));
}
public static void main(String[] args)
{
int N = 2;
leafNodeValues(N);
}
}
|
Python3
from math import ceil,log2
def leafNodeValues(N):
numberOfLeaves = (N - N // 2)
minDepth = ceil(log2(N + 1)) - 1;
N += 1
if (minDepth > 1 and (N & (N - 1))):
minDepth -= 1
print(numberOfLeaves, N - minDepth - 1)
if __name__ == '__main__':
N = 2
leafNodeValues(N)
|
C#
using System;
class GFG {
static void leafNodeValues(int N)
{
int numberOfLeaves = (N - N / 2);
int minDepth = (int)Math.Ceiling(Math.Log(N + 1) /
Math.Log(2)) - 1;
N++;
if (minDepth > 1 && (N & (N - 1)) != 0)
minDepth--;
Console.WriteLine(numberOfLeaves + " " +
(N - minDepth - 1));
}
static void Main()
{
int N = 2;
leafNodeValues(N);
}
}
|
Javascript
<script>
function log2(n)
{
return (Math.log(n)/Math.log(2));
}
function leafNodeValues(N)
{
let numberOfLeaves = parseInt((N - N / 2));
let minDepth = Math.ceil(log2(N + 1)) - 1;
N++;
if ((minDepth > 1) && (N & (N - 1)))
minDepth--;
document.write(numberOfLeaves);
document.write(' ');
document.write( N - minDepth - 1);
}
var N = 2;
leafNodeValues(N);
</script>
|
Time Complexity: O(log(N))
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...