Given a grid of numbers, find maximum length Snake sequence and print it. If multiple snake sequences exists with the maximum length, print any one of them.
A snake sequence is made up of adjacent numbers in the grid such that for each number, the number on the right or the number below it is +1 or -1 its value. For example, if you are at location (x, y) in the grid, you can either move right i.e. (x, y+1) if that number is ± 1 or move down i.e. (x+1, y) if that number is ± 1.
For example,
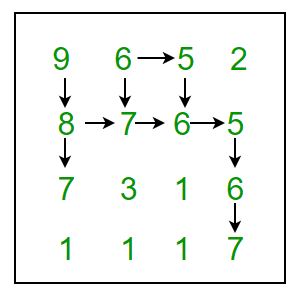
9, 6, 5, 2
8, 7, 6, 5
7, 3, 1, 6
1, 1, 1, 7
In above grid, the longest snake sequence is: (9, 8, 7, 6, 5, 6, 7)
Below figure shows all possible paths:
We strongly recommend you to minimize your browser and try this yourself first.
The idea is to use Dynamic Programming. For each cell of the matrix, we keep maximum length of a snake which ends in current cell. The maximum length snake sequence will have maximum value. The maximum value cell will correspond to tail of the snake. In order to print the snake, we need to backtrack from tail all the way back to snake’s head.
Let T[i][i] represent maximum length of a snake which ends at cell (i, j),
then for given matrix M, the DP relation is defined as
T[0][0] = 0
T[i][j] = max(T[i][j], T[i][j - 1] + 1) if M[i][j] = M[i][j - 1] ± 1
T[i][j] = max(T[i][j], T[i - 1][j] + 1) if M[i][j] = M[i - 1][j] ± 1
Below is the implementation of the idea
C++
#include <bits/stdc++.h>
using namespace std;
#define M 4
#define N 4
struct Point
{
int x, y;
};
list<Point> findPath(int grid[M][N], int mat[M][N],
int i, int j)
{
list<Point> path;
Point pt = {i, j};
path.push_front(pt);
while (grid[i][j] != 0)
{
if (i > 0 &&
grid[i][j] - 1 == grid[i - 1][j])
{
pt = {i - 1, j};
path.push_front(pt);
i--;
}
else if (j > 0 &&
grid[i][j] - 1 == grid[i][j - 1])
{
pt = {i, j - 1};
path.push_front(pt);
j--;
}
}
return path;
}
void findSnakeSequence(int mat[M][N])
{
int lookup[M][N];
memset(lookup, 0, sizeof lookup);
int max_len = 0;
int max_row = 0;
int max_col = 0;
for (int i = 0; i < M; i++)
{
for (int j = 0; j < N; j++)
{
if (i || j)
{
if (i > 0 &&
abs(mat[i - 1][j] - mat[i][j]) == 1)
{
lookup[i][j] = max(lookup[i][j],
lookup[i - 1][j] + 1);
if (max_len < lookup[i][j])
{
max_len = lookup[i][j];
max_row = i, max_col = j;
}
}
if (j > 0 &&
abs(mat[i][j - 1] - mat[i][j]) == 1)
{
lookup[i][j] = max(lookup[i][j],
lookup[i][j - 1] + 1);
if (max_len < lookup[i][j])
{
max_len = lookup[i][j];
max_row = i, max_col = j;
}
}
}
}
}
cout << "Maximum length of Snake sequence is: "
<< max_len << endl;
list<Point> path = findPath(lookup, mat, max_row,
max_col);
cout << "Snake sequence is:";
for (auto it = path.begin(); it != path.end(); it++)
cout << endl << mat[it->x][it->y] << " ("
<< it->x << ", " << it->y << ")" ;
}
int main()
{
int mat[M][N] =
{
{9, 6, 5, 2},
{8, 7, 6, 5},
{7, 3, 1, 6},
{1, 1, 1, 7},
};
findSnakeSequence(mat);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int M = 4;
static int N = 4;
static class Point
{
int x, y;
public Point(int x, int y)
{
this.x = x;
this.y = y;
}
};
static List<Point> findPath(int grid[][],
int mat[][],
int i, int j)
{
List<Point> path = new LinkedList<>();
Point pt = new Point(i, j);
path.add(0, pt);
while (grid[i][j] != 0)
{
if (i > 0 &&
grid[i][j] - 1 == grid[i - 1][j])
{
pt = new Point(i - 1, j);
path.add(0, pt);
i--;
}
else if (j > 0 && grid[i][j] - 1 ==
grid[i][j - 1])
{
pt = new Point(i, j - 1);
path.add(0, pt);
j--;
}
}
return path;
}
static void findSnakeSequence(int mat[][])
{
int [][]lookup = new int[M][N];
int max_len = 0;
int max_row = 0;
int max_col = 0;
for (int i = 0; i < M; i++)
{
for (int j = 0; j < N; j++)
{
if (i != 0 || j != 0)
{
if (i > 0 &&
Math.abs(mat[i - 1][j] -
mat[i][j]) == 1)
{
lookup[i][j] = Math.max(lookup[i][j],
lookup[i - 1][j] + 1);
if (max_len < lookup[i][j])
{
max_len = lookup[i][j];
max_row = i; max_col = j;
}
}
if (j > 0 &&
Math.abs(mat[i][j - 1] -
mat[i][j]) == 1)
{
lookup[i][j] = Math.max(lookup[i][j],
lookup[i][j - 1] + 1);
if (max_len < lookup[i][j])
{
max_len = lookup[i][j];
max_row = i; max_col = j;
}
}
}
}
}
System.out.print("Maximum length of Snake " +
"sequence is: " + max_len + "\n");
List<Point> path = findPath(lookup, mat, max_row,
max_col);
System.out.print("Snake sequence is:");
for (Point it : path)
System.out.print("\n" + mat[it.x][it.y] + " (" +
it.x + ", " + it.y + ")");
}
public static void main(String[] args)
{
int mat[][] = {{9, 6, 5, 2},
{8, 7, 6, 5},
{7, 3, 1, 6},
{1, 1, 1, 7}};
findSnakeSequence(mat);
}
}
|
C#
using System;
using System.Collections.Generic;
class GFG {
static int M = 4;
static int N = 4;
public class Point {
public int x, y;
public Point(int x, int y)
{
this.x = x;
this.y = y;
}
};
static List<Point> findPath(int[, ] grid, int[, ] mat,
int i, int j)
{
List<Point> path = new List<Point>();
Point pt = new Point(i, j);
path.Insert(0, pt);
while (grid[i, j] != 0) {
if (i > 0 && grid[i, j] - 1 == grid[i - 1, j]) {
pt = new Point(i - 1, j);
path.Insert(0, pt);
i--;
}
else if (j > 0
&& grid[i, j] - 1 == grid[i, j - 1]) {
pt = new Point(i, j - 1);
path.Insert(0, pt);
j--;
}
}
return path;
}
static void findSnakeSequence(int[, ] mat)
{
int[, ] lookup = new int[M, N];
int max_len = 0;
int max_row = 0;
int max_col = 0;
for (int i = 0; i < M; i++) {
for (int j = 0; j < N; j++) {
if (i != 0 || j != 0) {
if (i > 0
&& Math.Abs(mat[i - 1, j]
- mat[i, j])
== 1) {
lookup[i, j] = Math.Max(
lookup[i, j],
lookup[i - 1, j] + 1);
if (max_len < lookup[i, j]) {
max_len = lookup[i, j];
max_row = i;
max_col = j;
}
}
if (j > 0
&& Math.Abs(mat[i, j - 1]
- mat[i, j])
== 1) {
lookup[i, j] = Math.Max(
lookup[i, j],
lookup[i, j - 1] + 1);
if (max_len < lookup[i, j]) {
max_len = lookup[i, j];
max_row = i;
max_col = j;
}
}
}
}
}
Console.Write("Maximum length of Snake "
+ "sequence is: " + max_len + "\n");
List<Point> path
= findPath(lookup, mat, max_row, max_col);
Console.Write("Snake sequence is:");
foreach(Point it in path)
Console.Write("\n" + mat[it.x, it.y] + " ("
+ it.x + ", " + it.y + ")");
}
public static void Main(String[] args)
{
int[, ] mat = { { 9, 6, 5, 2 },
{ 8, 7, 6, 5 },
{ 7, 3, 1, 6 },
{ 1, 1, 1, 7 } };
findSnakeSequence(mat);
}
}
|
Python3
def snakesequence(S, m, n):
sequence = {}
DP = [[1 for x in range(m+1)] for x in range(n+1)]
a, b, maximum = 0, 0, 0
position = [0, 0]
for i in range(0, n+1):
for j in range(0, m+1):
a, b = 0, 0
p = "initial"
if(i > 0 and abs(S[i][j] - S[i-1][j]) == 1):
a = DP[i-1][j]
if(j > 0 and abs(S[i][j] - S[i][j-1]) == 1):
b = DP[i][j-1]
if a != 0 and a >= b:
p = str(i-1) + " " + str(j)
elif b != 0:
p = str(i) + " " + str(j-1)
q = str(i) + " " + str(j)
sequence[q] = p
DP[i][j] = DP[i][j] + max(a, b)
if DP[i][j] >= maximum:
maximum = DP[i][j]
position[0] = i
position[1] = j
snakeValues = []
snakePositions = []
snakeValues.append(S[position[0]][position[1]])
check = 'found'
str_next = str(position[0]) + " " + str(position[1])
findingIndices = sequence[str_next].split()
while(check == 'found'):
if sequence[str_next] == 'initial':
snakePositions.insert(0, str_next)
check = 'end'
continue
findingIndices = sequence[str_next].split()
g = int(findingIndices[0])
h = int(findingIndices[1])
snakeValues.insert(0, S[g][h])
snake_position = str(g) + " " + str(h)
snakePositions.insert(0, str_next)
str_next = sequence[str_next]
return [snakeValues, snakePositions]
S = [[9, 6, 5, 2],
[8, 7, 6, 5],
[7, 3, 1, 6],
[1, 1, 10, 7]]
m = 3
n = 3
seq = snakesequence(S, m, n)
for i in range(len(seq[0])):
print(seq[0][i], ",", seq[1][i].split())
|
Javascript
function snakesequence(S, m, n)
{
let sequence = {}
let DP = new Array(n + 1)
for (var i = 0; i <= n; i++)
DP[i] = new Array(m + 1).fill(1)
let a = 0, b = 0, maximum = 0
let position = [0, 0]
for (var i = 0; i <= n; i++)
{
for (var j = 0; j <= m; j++)
{
a = 0
b = 0
let p = "initial"
if(i > 0 && Math.abs(S[i][j] - S[i-1][j]) == 1)
a = DP[i-1][j]
if(j > 0 && Math.abs(S[i][j] - S[i][j-1]) == 1)
b = DP[i][j-1]
if (a != 0 && a >= b)
p = String(i-1) + " " + String(j)
else if (b != 0)
p = String(i) + " " + String(j-1)
let q = String(i) + " " + String(j)
sequence[q] = p
DP[i][j] = DP[i][j] + Math.max(a, b)
if (DP[i][j] >= maximum)
{
maximum = DP[i][j]
position[0] = i
position[1] = j
}
}
}
let snakeValues = []
let snakePositions = []
snakeValues.push(S[position[0]][position[1]])
let check = 'found'
let String_next = String(position[0]) + " " + String(position[1])
let findingIndices = sequence[String_next].split(" ")
while(check == 'found')
{
if (sequence[String_next] == 'initial')
{
snakePositions.unshift(String_next)
check = 'end'
continue
}
findingIndices = sequence[String_next].split(" ")
let g = parseInt(findingIndices[0])
let h = parseInt(findingIndices[1])
snakeValues.unshift(S[g][h])
let snake_position = String(g) + " " + String(h)
snakePositions.unshift(String_next)
String_next = sequence[String_next]
}
return [snakeValues, snakePositions]
}
let S = [[9, 6, 5, 2],
[8, 7, 6, 5],
[7, 3, 1, 6],
[1, 1, 10, 7]]
let m = 3
let n = 3
let seq = snakesequence(S, m, n)
for (var i = 0; i < seq[0].length; i++)
console.log(seq[0][i] + ",", seq[1][i].split(" "))
|
OutputMaximum length of Snake sequence is: 6
Snake sequence is:
9 (0, 0)
8 (1, 0)
7 (1, 1)
6 (1, 2)
5 (1, 3)
6 (2, 3)
7 (3, 3)
Time complexity of above solution is O(M*N). Auxiliary space used by above solution is O(M*N). If we are not required to print the snake, space can be further reduced to O(N) as we only uses the result from last row.
This article is contributed by Aditya Goel. If you like GeeksforGeeks and would like to contribute, you can also write an article and mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.