Find k-cores of an undirected graph
Last Updated :
27 Mar, 2023
Given a graph G and an integer K, K-cores of the graph are connected components that are left after all vertices of degree less than k have been removed (Source wiki)
Example:
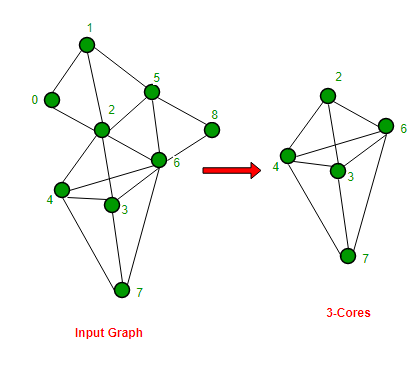
Input : Adjacency list representation of graph shown
on left side of below diagram
Output: K-Cores :
[2] -> 3 -> 4 -> 6
[3] -> 2 -> 4 -> 6 -> 7
[4] -> 2 -> 3 -> 6 -> 7
[6] -> 2 -> 3 -> 4 -> 7
[7] -> 3 -> 4 -> 6
We strongly recommend you to minimize your browser and try this yourself first.
The standard algorithm to find a k-core graph is to remove all the vertices that have degree less than- ‘K’ from the input graph. We must be careful that removing a vertex reduces the degree of all the vertices adjacent to it, hence the degree of adjacent vertices can also drop below-‘K’. And thus, we may have to remove those vertices also. This process may/may not go until there are no vertices left in the graph.
To implement above algorithm, we do a modified DFS on the input graph and delete all the vertices having degree less than ‘K’, then update degrees of all the adjacent vertices, and if their degree falls below ‘K’ we will delete them too.
Below is implementation of above idea. Note that the below program only prints vertices of k cores, but it can be easily extended to print the complete k cores as we have modified adjacency list.
C++14
#include<bits/stdc++.h>
using namespace std;
class Graph
{
int V;
list<int> *adj;
public:
Graph(int V);
void addEdge(int u, int v);
bool DFSUtil(int, vector<bool> &, vector<int> &, int k);
void printKCores(int k);
};
bool Graph::DFSUtil(int v, vector<bool> &visited,
vector<int> &vDegree, int k)
{
visited[v] = true;
list<int>::iterator i;
for (i = adj[v].begin(); i != adj[v].end(); ++i)
{
if (vDegree[v] < k)
vDegree[*i]--;
if (!visited[*i])
{
DFSUtil(*i, visited, vDegree, k);
}
}
return (vDegree[v] < k);
}
Graph::Graph(int V)
{
this->V = V;
adj = new list<int>[V];
}
void Graph::addEdge(int u, int v)
{
adj[u].push_back(v);
adj[v].push_back(u);
}
void Graph::printKCores(int k)
{
vector<bool> visited(V, false);
vector<bool> processed(V, false);
int mindeg = INT_MAX;
int startvertex;
vector<int> vDegree(V);
for (int i=0; i<V; i++)
{
vDegree[i] = adj[i].size();
if (vDegree[i] < mindeg)
{
mindeg = vDegree[i];
startvertex=i;
}
}
DFSUtil(startvertex, visited, vDegree, k);
for (int i=0; i<V; i++)
if (visited[i] == false)
DFSUtil(i, visited, vDegree, k);
for (int v=0; v<V; v++){
if (vDegree[v] >= k){
int cnt = 0;
list<int>::iterator itr;
for (itr = adj[v].begin(); itr != adj[v].end(); ++itr)
if (vDegree[*itr] >= k)
cnt++;
if(cnt < k)
vDegree[v] = cnt;
}
}
cout << "K-Cores : \n";
for (int v=0; v<V; v++)
{
if (vDegree[v] >= k)
{
cout << "\n[" << v << "]";
list<int>::iterator itr;
for (itr = adj[v].begin(); itr != adj[v].end(); ++itr)
if (vDegree[*itr] >= k)
cout << " -> " << *itr;
}
}
}
int main()
{
int k = 3;
Graph g1(9);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(1, 5);
g1.addEdge(2, 3);
g1.addEdge(2, 4);
g1.addEdge(2, 5);
g1.addEdge(2, 6);
g1.addEdge(3, 4);
g1.addEdge(3, 6);
g1.addEdge(3, 7);
g1.addEdge(4, 6);
g1.addEdge(4, 7);
g1.addEdge(5, 6);
g1.addEdge(5, 8);
g1.addEdge(6, 7);
g1.addEdge(6, 8);
g1.printKCores(k);
cout << endl << endl;
Graph g2(13);
g2.addEdge(0, 1);
g2.addEdge(0, 2);
g2.addEdge(0, 3);
g2.addEdge(1, 4);
g2.addEdge(1, 5);
g2.addEdge(1, 6);
g2.addEdge(2, 7);
g2.addEdge(2, 8);
g2.addEdge(2, 9);
g2.addEdge(3, 10);
g2.addEdge(3, 11);
g2.addEdge(3, 12);
g2.printKCores(k);
Graph gr(9);
gr.addEdge(0, 1);
gr.addEdge(0, 2);
gr.addEdge(1, 2);
gr.addEdge(2, 5);
gr.addEdge(2, 4);
gr.addEdge(2, 3);
gr.addEdge(2, 6);
gr.addEdge(3, 4);
gr.addEdge(3, 6);
gr.addEdge(3, 7);
gr.addEdge(4, 6);
gr.addEdge(5, 6);
gr.addEdge(5, 7);
gr.addEdge(5, 8);
gr.addEdge(8, 7);
gr.printKCores(k);
return 0;
}
|
Java
import java.util.*;
class GFG
{
static class Graph
{
int V;
Vector<Integer>[] adj;
@SuppressWarnings("unchecked")
Graph(int V)
{
this.V = V;
this.adj = new Vector[V];
for (int i = 0; i < V; i++)
adj[i] = new Vector<>();
}
void addEdge(int u, int v)
{
this.adj[u].add(v);
this.adj[v].add(u);
}
boolean DFSUtil(int v, boolean[] visited, int[] vDegree, int k)
{
visited[v] = true;
for (int i : adj[v])
{
if (vDegree[v] < k)
vDegree[i]--;
if (!visited[i])
{
DFSUtil(i, visited, vDegree, k);
}
}
return (vDegree[v] < k);
}
void printKCores(int k)
{
boolean[] visited = new boolean[V];
boolean[] processed = new boolean[V];
Arrays.fill(visited, false);
Arrays.fill(processed, false);
int mindeg = Integer.MAX_VALUE;
int startvertex = 0;
int[] vDegree = new int[V];
for (int i = 0; i < V; i++)
{
vDegree[i] = adj[i].size();
if (vDegree[i] < mindeg)
{
mindeg = vDegree[i];
startvertex = i;
}
}
DFSUtil(startvertex, visited, vDegree, k);
for (int i = 0; i < V; i++)
if (!visited[i])
DFSUtil(i, visited, vDegree, k);
System.out.println("K-Cores : ");
for (int v = 0; v < V; v++)
{
if (vDegree[v] >= k)
{
System.out.printf("\n[%d]", v);
for (int i : adj[v])
if (vDegree[i] >= k)
System.out.printf(" -> %d", i);
}
}
}
}
public static void main(String[] args)
{
int k = 3;
Graph g1 = new Graph(9);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(1, 5);
g1.addEdge(2, 3);
g1.addEdge(2, 4);
g1.addEdge(2, 5);
g1.addEdge(2, 6);
g1.addEdge(3, 4);
g1.addEdge(3, 6);
g1.addEdge(3, 7);
g1.addEdge(4, 6);
g1.addEdge(4, 7);
g1.addEdge(5, 6);
g1.addEdge(5, 8);
g1.addEdge(6, 7);
g1.addEdge(6, 8);
g1.printKCores(k);
System.out.println();
Graph g2 = new Graph(13);
g2.addEdge(0, 1);
g2.addEdge(0, 2);
g2.addEdge(0, 3);
g2.addEdge(1, 4);
g2.addEdge(1, 5);
g2.addEdge(1, 6);
g2.addEdge(2, 7);
g2.addEdge(2, 8);
g2.addEdge(2, 9);
g2.addEdge(3, 10);
g2.addEdge(3, 11);
g2.addEdge(3, 12);
g2.printKCores(k);
}
}
|
Python3
from collections import defaultdict
class Graph:
def __init__(self):
self.graph = defaultdict(list)
def addEdge(self, u, v):
self.graph[u].append(v)
self.graph[v].append(u)
def DFSUtil(self, v, visited, vDegree, k):
visited.add(v)
for i in self.graph[v]:
if vDegree[v] < k:
vDegree[i] = vDegree[i] - 1
if i not in visited:
self.DFSUtil(i, visited, vDegree, k)
def PrintKCores(self, k):
visit = set()
degree = defaultdict(lambda: 0)
for i in list(self.graph):
degree[i] = len(self.graph[i])
for i in list(self.graph):
if i not in visit:
self.DFSUtil(i, visit, degree, k)
for i in list(self.graph):
if degree[i] >= k:
print(str("\n [ ") + str(i) + str(" ]"), end=" ")
for j in self.graph[i]:
if degree[j] >= k:
print("-> " + str(j), end=" ")
print()
k = 3
g1 = Graph()
g1.addEdge(0, 1)
g1.addEdge(0, 2)
g1.addEdge(1, 2)
g1.addEdge(1, 5)
g1.addEdge(2, 3)
g1.addEdge(2, 4)
g1.addEdge(2, 5)
g1.addEdge(2, 6)
g1.addEdge(3, 4)
g1.addEdge(3, 6)
g1.addEdge(3, 7)
g1.addEdge(4, 6)
g1.addEdge(4, 7)
g1.addEdge(5, 6)
g1.addEdge(5, 8)
g1.addEdge(6, 7)
g1.addEdge(6, 8)
g1.PrintKCores(k)
|
C#
using System;
using System.Collections.Generic;
class GFG{
public class Graph
{
int V;
List<int>[] adj;
public Graph(int V)
{
this.V = V;
this.adj = new List<int>[V];
for(int i = 0; i < V; i++)
adj[i] = new List<int>();
}
public void addEdge(int u, int v)
{
this.adj[u].Add(v);
this.adj[v].Add(u);
}
bool DFSUtil(int v, bool[] visited,
int[] vDegree, int k)
{
visited[v] = true;
foreach (int i in adj[v])
{
if (vDegree[v] < k)
vDegree[i]--;
if (!visited[i])
{
DFSUtil(i, visited, vDegree, k);
}
}
return (vDegree[v] < k);
}
public void printKCores(int k)
{
bool[] visited = new bool[V];
int mindeg = int.MaxValue;
int startvertex = 0;
int[] vDegree = new int[V];
for(int i = 0; i < V; i++)
{
vDegree[i] = adj[i].Count;
if (vDegree[i] < mindeg)
{
mindeg = vDegree[i];
startvertex = i;
}
}
DFSUtil(startvertex, visited, vDegree, k);
for(int i = 0; i < V; i++)
if (!visited[i])
DFSUtil(i, visited, vDegree, k);
Console.WriteLine("K-Cores : ");
for(int v = 0; v < V; v++)
{
if (vDegree[v] >= k)
{
Console.Write("\n " + v);
foreach(int i in adj[v])
if (vDegree[i] >= k)
Console.Write(" -> " + i);
}
}
}
}
public static void Main(String[] args)
{
int k = 3;
Graph g1 = new Graph(9);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(1, 5);
g1.addEdge(2, 3);
g1.addEdge(2, 4);
g1.addEdge(2, 5);
g1.addEdge(2, 6);
g1.addEdge(3, 4);
g1.addEdge(3, 6);
g1.addEdge(3, 7);
g1.addEdge(4, 6);
g1.addEdge(4, 7);
g1.addEdge(5, 6);
g1.addEdge(5, 8);
g1.addEdge(6, 7);
g1.addEdge(6, 8);
g1.printKCores(k);
Console.WriteLine();
Graph g2 = new Graph(13);
g2.addEdge(0, 1);
g2.addEdge(0, 2);
g2.addEdge(0, 3);
g2.addEdge(1, 4);
g2.addEdge(1, 5);
g2.addEdge(1, 6);
g2.addEdge(2, 7);
g2.addEdge(2, 8);
g2.addEdge(2, 9);
g2.addEdge(3, 10);
g2.addEdge(3, 11);
g2.addEdge(3, 12);
g2.printKCores(k);
}
}
|
Javascript
class Graph {
constructor(V) {
this.V = V;
this.adj = new Array(V);
for (let i = 0; i < V; i++) {
this.adj[i] = new Array();
}
}
addEdge(u, v) {
this.adj[u].push(v);
this.adj[v].push(u);
}
DFSUtil(v, visited, vDegree, k) {
visited[v] = true;
for (let i of this.adj[v]) {
if (vDegree[v] < k)
vDegree[i]--;
if (!visited[i])
{
this.DFSUtil(i, visited, vDegree, k);
}
}
return vDegree[v] < k;
}
printKCores(k) {
let visited = new Array(this.V).fill(false);
let processed = new Array(this.V).fill(false);
let mindeg = Number.MAX_VALUE;
let startvertex = 0;
let vDegree = new Array(this.V);
for (let i = 0; i < this.V; i++)
{
vDegree[i] = this.adj[i].length;
if (vDegree[i] < mindeg)
{
mindeg = vDegree[i];
startvertex = i;
}
}
this.DFSUtil(startvertex, visited, vDegree, k);
for (let i = 0; i < this.V; i++)
if (!visited[i])
this.DFSUtil(i, visited, vDegree, k);
console.log("K-Cores : ");
for (let v = 0; v < this.V; v++) {
if (vDegree[v] >= k) {
console.log(`\n[${v}]`);
for (let i of this.adj[v])
if (vDegree[i] >= k) console.log(` -> ${i}`);
}
}
}
}
let k = 3;
let g1 = new Graph(9);
g1.addEdge(0, 1);
g1.addEdge(0, 2);
g1.addEdge(1, 2);
g1.addEdge(1, 5);
g1.addEdge(2, 3);
g1.addEdge(2, 4);
g1.addEdge(2, 5);
g1.addEdge(2, 6);
g1.addEdge(3, 4);
g1.addEdge(3, 6);
g1.addEdge(3, 7);
g1.addEdge(4, 6);
g1.addEdge(4, 7);
g1.addEdge(5, 6);
g1.addEdge(5, 8);
g1.addEdge(6, 7);
g1.addEdge(6, 8);
g1.printKCores(k);
console.log();
let g2 = new Graph(13);
g2.addEdge(0, 1);
g2.addEdge(0, 2);
g2.addEdge(0, 3);
g2.addEdge(1, 4);
g2.addEdge(1, 5);
g2.addEdge(1, 6);
g2.addEdge(2, 7);
g2.addEdge(2, 8);
g2.addEdge(2, 9);
g2.addEdge(3, 10);
g2.addEdge(3, 11);
g2.addEdge(3, 12);
g2.printKCores(k);
|
Output
K-Cores :
[2] -> 3 -> 4 -> 6
[3] -> 2 -> 4 -> 6 -> 7
[4] -> 2 -> 3 -> 6 -> 7
[6] -> 2 -> 3 -> 4 -> 7
[7] -> 3 -> 4 -> 6
K-Cores :
K-Cores :
[2] -> 4 -> 3 -> 6
[3] -> 2 -> 4 -> 6
[4] -> 2 -> 3 -> 6
[6] -> 2 -> 3 -> 4
Time complexity: O(V + E), Where V is number of vertices and E is number of edges.
Auxiliary Space: O(V)
The extra space is used for the visited array.
Related Concepts :
Degeneracy : Degeneracy of a graph is the largest value k such that the graph has a k-core. For example, the above shown graph has a 3-Cores and doesn’t have 4 or higher cores. Therefore, above graph is 3-degenerate.
Degeneracy of a graph is used to measure how sparse graph is.
Reference :
https://en.wikipedia.org/wiki/Degeneracy_%28graph_theory%29
Share your thoughts in the comments
Please Login to comment...