Find K consecutive integers such that their sum is N
Last Updated :
09 Aug, 2022
Given two integers N and K, the task is to find K consecutive integers such that their sum if N.
Note: If there is no such K integers print -1.
Examples:
Input: N = 15, K = 5
Output: 1 2 3 4 5
Explanation:
N can be represented as sum of 5 consecutive integers as follows –
=> N => 1 + 2 + 3 + 4 + 5 = 15
Input: N = 33, K = 6
Output: 3 4 5 6 7 8
Explanation:
N can be represented as sum of 6 consecutive integers as follows –
=> N => 3 + 4 + 5 + 6 + 7 + 8 = 33
Naive Approach: A simple solution is to run a loop from i = 0 to N – (K – 1) to check if K consecutive integers starting from i is having sum as N.
Efficient Approach: The idea is to use Arithmetic Progression to solve this problem, where sum of K terms of arithmetic progression with common difference is 1 can be defined as follows –
- Sum of K Terms –

=> 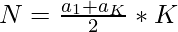
- Solving the equation further to get the first term possible
=> 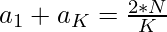
- Here aK is the Kth term which can be written as a1 + K – 1
=> 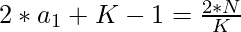
=> 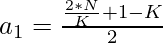
- Finally, check the first term computed is an integer, If yes then K consecutive number exists whose sum if N.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void checksum(int n, int k)
{
float first_term = ((2 * n) / k
+ (1 - k))
/ 2.0;
if (first_term - int(first_term) == 0) {
for (int i = first_term;
i <= first_term + k - 1; i++) {
cout << i << " ";
}
}
else
cout << "-1";
}
int main()
{
int n = 33, k = 6;
checksum(n, k);
return 0;
}
|
Java
class GFG{
static void checksum(int n, int k)
{
float first_term = (float) (((2 * n) / k +
(1 - k)) / 2.0);
if (first_term - (int)(first_term) == 0)
{
for(int i = (int)first_term;
i <= first_term + k - 1; i++)
{
System.out.print(i + " ");
}
}
else
System.out.print("-1");
}
public static void main(String[] args)
{
int n = 33, k = 6;
checksum(n, k);
}
}
|
Python3
def checksum(n, k):
first_term = ((2 * n) / k + (1 - k)) / 2.0
if (first_term - int(first_term) == 0):
for i in range(int(first_term),
int(first_term) + k):
print(i, end = ' ')
else:
print('-1')
if __name__=='__main__':
(n, k) = (33, 6)
checksum(n, k)
|
C#
using System;
class GFG{
static void checksum(int n, int k)
{
float first_term = (float)(((2 * n) / k +
(1 - k)) / 2.0);
if (first_term - (int)(first_term) == 0)
{
for(int i = (int)first_term;
i <= first_term + k - 1; i++)
{
Console.Write(i + " ");
}
}
else
Console.Write("-1");
}
public static void Main(String[] args)
{
int n = 33, k = 6;
checksum(n, k);
}
}
|
Javascript
<script>
function checksum(n , k)
{
var first_term = (((2 * n) / k + (1 - k)) / 2.0);
if (first_term - parseInt( (first_term)) == 0) {
for (i = parseInt( first_term); i <= first_term + k - 1; i++) {
document.write(i + " ");
}
} else
document.write("-1");
}
var n = 33, k = 6;
checksum(n, k);
</script>
|
Time Complexity: O(n)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...