Given an array A of size N where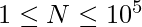 
. The task is to find the AND of all possible sub-arrays of A and then the AND of all these results.
Examples:
Input : 1 2 3
Output : 0
All possible subarrays are
{1}, {2}, {3}, {1, 2}, {2, 3} and {1, 2, 3}
ANDs of these subarrays are 1, 2, 3, 0, 2, 0.
AND of these ANDs is 0.
Input : 100 500 1000
Output : 96
Approach: The Naive solution is to find the AND of all the sub-arrays and then print the AND of their results. This will lead to O(N2) solution.
Optimal Solution: Using the properties of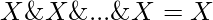 
i:e it doesn’t matter how many times an element comes, its ANDing will be counted as one only. Thus, our problem is reduced to finding the AND of all the elements of the array only.
Implementation:
C++
#include <bits/stdc++.h>
using namespace std;
int AND(int a[], int n)
{
int ans = a[0];
for (int i = 0; i < n; ++i)
ans &= a[i];
return ans;
}
int main()
{
int a[] = { 1, 2, 3 };
int n = sizeof(a) / sizeof(a[0]);
cout << AND(a, n);
return 0;
}
|
Java
public class GFG {
static int AND(int a[], int n)
{
int ans = a[0];
for (int i = 0; i < n; ++i)
ans &= a[i];
return ans;
}
public static void main(String[] args) {
int a[] = { 1, 2, 3 };
int n = a.length;
System.out.println(AND(a, n));
}
}
|
Python 3
def AND(arr, n) :
res = arr[0]
for i in range(1, n):
res &= arr[i]
if res == 0:
return 0
return res
if __name__ == "__main__" :
a = [ 100, 500, 1000]
n = len(a)
print(AND(a, n))
|
C#
using System;
public class GFG {
static int AND(int []a, int n)
{
int ans = a[0];
for (int i = 0; i < n; ++i)
ans &= a[i];
return ans;
}
public static void Main() {
int []a = { 1, 2, 3 };
int n = a.Length;
Console.WriteLine(AND(a, n));
}
}
|
PHP
<?php
function ANDS(&$a, $n)
{
$ans = $a[0];
for ($i = 0; $i < $n; ++$i)
$ans &= $a[$i];
return $ans;
}
$a = array( 1, 2, 3 );
$n = sizeof($a);
echo ANDS($a, $n);
?>
|
Javascript
<script>
function AND(a,n)
{
let ans = a[0];
for (let i = 0; i < n; ++i)
ans &= a[i];
return ans;
}
let a=[ 1, 2, 3 ];
let n = a.length;
document.write(AND(a, n));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Approach: Finding AND of all subarrays using bit manipulation and hashing.
We can use the bitwise AND operator to get the AND of all sub-arrays. The idea is to count the number of times each bit is set in the sub-arrays. If a bit is set in all the sub-arrays, then it will be set in the result. We can use a hash table to count the number of times each bit is set. Then, we can check if the bit is set in all the sub-arrays or not.
Algorithm:
- Initialize a hash table to count the number of times each bit is set.
- Traverse the array and for each element, traverse all the bits and if the bit is set, increment the count of that bit in the hash table.
- Initialize the result variable to 0.
- Traverse the hash table and for each bit, if the count is equal to the length of the array, set the bit in the result variable.
- Return the result variable.
Here is the implementation of above algorithm:-
C++
#include <iostream>
#include <unordered_map>
using namespace std;
int AND(int arr[], int n) {
unordered_map<int, int> bit_count;
for (int i = 0; i < n; i++) {
int num = arr[i];
int pos = 0;
while (num > 0) {
if (num & 1) {
if (bit_count.find(pos) == bit_count.end()) {
bit_count[pos] = 1;
} else {
bit_count[pos]++;
}
}
num >>= 1;
pos++;
}
}
int res = 0;
for (auto it : bit_count) {
if (it.second == n) {
res |= (1 << it.first);
}
}
return res;
}
int main() {
int arr[] = {1, 2, 3};
int n = sizeof(arr)/sizeof(arr[0]);
cout << AND(arr, n) << endl;
return 0;
}
|
Java
import java.util.HashMap;
import java.util.Map;
public class Main {
static int AND(int[] arr) {
int n = arr.length;
Map<Integer, Integer> bit_count = new HashMap<>();
for (int i = 0; i < n; i++) {
int num = arr[i];
int pos = 0;
while (num > 0) {
if ((num & 1) == 1) {
if (!bit_count.containsKey(pos)) {
bit_count.put(pos, 1);
} else {
bit_count.put(pos, bit_count.get(pos) + 1);
}
}
num >>= 1;
pos++;
}
}
int res = 0;
for (Map.Entry<Integer, Integer> entry : bit_count.entrySet()) {
if (entry.getValue() == n) {
res |= (1 << entry.getKey());
}
}
return res;
}
public static void main(String[] args) {
int[] arr = {1, 2, 3};
System.out.println(AND(arr));
}
}
|
Python
def AND(arr):
n = len(arr)
bit_count = {}
for i in range(n):
num = arr[i]
pos = 0
while num > 0:
if num & 1:
if pos not in bit_count:
bit_count[pos] = 1
else:
bit_count[pos] += 1
num >>= 1
pos += 1
res = 0
for bit, count in bit_count.items():
if count == n:
res |= (1 << bit)
return res
arr = [1, 2, 3]
print(AND(arr))
|
C#
using System;
using System.Collections.Generic;
public class Program {
static int AND(int[] arr) {
int n = arr.Length;
Dictionary<int, int> bit_count = new Dictionary<int, int>();
for (int i = 0; i < n; i++) {
int num = arr[i];
int pos = 0;
while (num > 0) {
if ((num & 1) == 1) {
if (!bit_count.ContainsKey(pos)) {
bit_count.Add(pos, 1);
} else {
bit_count[pos]++;
}
}
num >>= 1;
pos++;
}
}
int res = 0;
foreach (KeyValuePair<int, int> pair in bit_count) {
if (pair.Value == n) {
res |= (1 << pair.Key);
}
}
return res;
}
static void Main(string[] args) {
int[] arr1 = new int[] { 1, 2, 3 };
Console.WriteLine(AND(arr1));
int[] arr2 = new int[] { 100, 500, 1000 };
Console.WriteLine(AND(arr2));
}
}
|
Javascript
function AND(arr) {
const n = arr.length;
const bit_count = new Map();
for (let i = 0; i < n; i++) {
let num = arr[i];
let pos = 0;
while (num > 0) {
if (num & 1) {
if (!bit_count.has(pos)) {
bit_count.set(pos, 1);
} else {
bit_count.set(pos, bit_count.get(pos) + 1);
}
}
num >>= 1;
pos++;
}
}
let res = 0;
for (let [bit, count] of bit_count) {
if (count === n) {
res |= (1 << bit);
}
}
return res;
}
const arr1 = [1, 2, 3];
console.log(AND(arr1));
const arr2 = [100, 500, 1000];
console.log(AND(arr2));
|
The Time complexity of this approach is O(N * L), where N is the length of the input array and L is the maximum number of bits required to represent any number in the array.
The Space complexity of this approach is also O(L), as we are using a dictionary to store the count of set bits for each position.