Factorized Random Synthesizer
Last Updated :
05 Jun, 2021
Transformer models are a huge success among the wide range of different NLP tasks. This caused the transformers to largely replacing the former auto-regressive recurrent neural network architecture in many state-of-the-art architectures. At the core of this transformer, the architecture uses a method called Query-Key dot product attention. The success of this transformer architecture is mostly attributed to the self-attention mechanism.
The factorized random dense synthesizer is a type of attention model that is proposed in the paper ‘Synthesizer: Rethinking Self Attention For Transformer Models ‘ by Google Research. The motivation behind this is to reduce the time complexity of the architecture operation by proposing the alternatives of dot-product self-attention.
Random Synthesizer
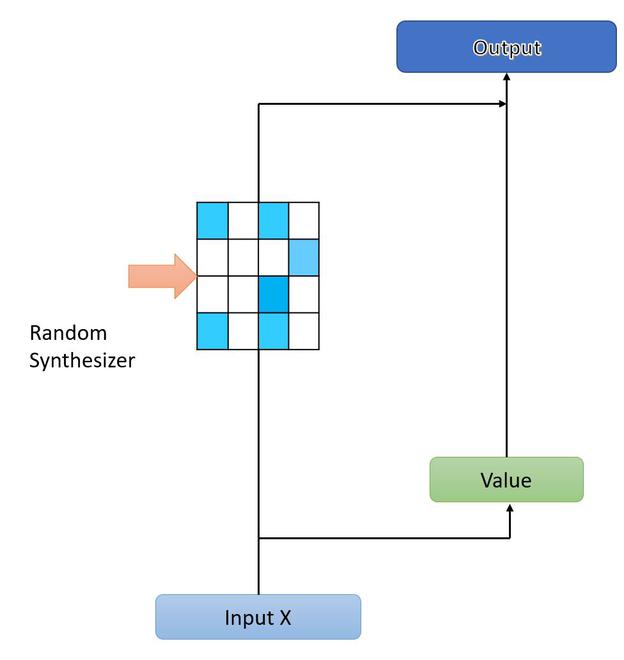
Random Synthesizer
The Dense Synthesizer version learns synthetic attention by condition on each input for X and projecting the input to l dimension. This means that Dense Synthesizer conditioned on each topic independently contrastingly different from the original transformer architecture in which we processed all tokens at one. The authors proposed another synthesizer in which the attention weights are initialized to random values instead of conditioning on any input. These random attention weights can either be trainable or fixed.
Let’s take R as a randomly initialized matrix. The random synthesizer can be defined as :
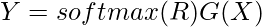
where R ∈ Rl*l , Each head increases the number of parameters in the network by l2.
The basic idea behind the randomized synthesizer is to remove the dependence of pairwise token interaction or any other information on a given token instead learns a task-specific alignment that works globally across different samples.
Factorized random synthesizer
The random synthesizer adds l*l parameters to the network, this makes it even harder to train the Dense Synthesizer when the value of l becomes large. Despite removing the key and query matrices, this model can be difficult to train. Thus, the author proposes the factorized versions of these synthesizers.
In this method, the author factorizes the R into the low-rank matrices R1 and R2 such that R1, R2 ∈ Rl*k.

From the above equation, it can be easily computed that for each head the parameter cost reduces from l2 to 2lk where k<<l.
Mixtures of Synthesizers
We can combine all the proposed synthetic attention variants in an additive fashion. This expression for this is:
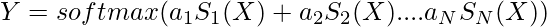
where S is the parameterization function, a is parameter such that \sum a =1 that is the trainable weight.
In the case of mixing random factorized random and standard dense synthesis, the expression becomes:
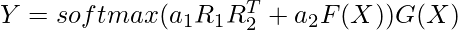
Time Complexity:
The time complexity of Self-attention is \theta = 2d^{2} while for the Random Synthesizer, the time complexity becomes \theta(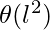 and factorized random synthesizer, the time complexity is
and factorized random synthesizer, the time complexity is 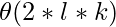 . Where l refers to sequence length, d is the dimensionality of the model & k is factorization.
. Where l refers to sequence length, d is the dimensionality of the model & k is factorization.
References
Share your thoughts in the comments
Please Login to comment...