Expression Trees Using Classes in C++ with Implementation
Last Updated :
25 Nov, 2022
Prerequisite: Expression Tree
The expression tree is a binary tree in which each internal node corresponds to the operator and each leaf node corresponds to the operand so for example expression tree for 3 + ((5+9)*2) would be:
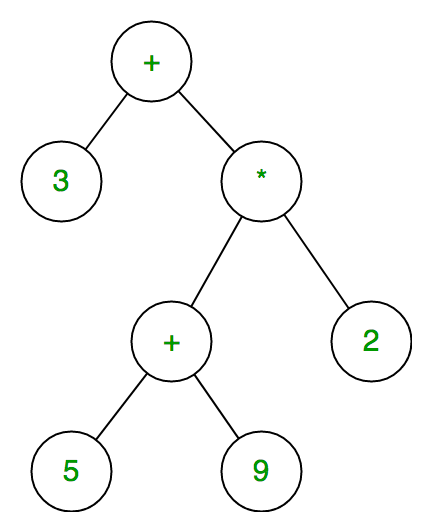
In expression trees, leaf nodes are operands and non-leaf nodes are operators. That means an expression tree is a binary tree where internal nodes are operators and leaves are operands. An expression tree consists of binary expressions. But for a unary operator, one subtree will be empty.
Construction of Expression Tree:
- The user will provide a postfix expression for which the program will construct the expression tree.
- Inorder traversal of binary tree/expression tree will provide Infix expression of the given input.
Example:
Input: A B C*+ D/
Output: A + B * C / D
Step 1: The first three symbols are operands, so create tree nodes and push pointers to them onto a stack as shown below.

Step 2: In the Next step, an operator ‘*’ will going read, so two pointers to trees are popped, a new tree is formed and a pointer to it is pushed onto the stack

Step 3: In the Next step, an operator ‘+’ will read, so two pointers to trees are popped, a new tree is formed and a pointer to it is pushed onto the stack.

Step 4: Similarly, as above cases first we push ‘D’ into the stack and then in the last step first, will read ‘/’ and then as previous step topmost element will pop out and then will be right subtree of root ‘/’ and other node will be right subtree.
Final Constructed Expression Tree is:

Below is the C++ program to implement the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
class node {
public:
char value;
node* left;
node* right;
node* next = NULL;
node(char c)
{
this->value = c;
left = NULL;
right = NULL;
}
node()
{
left = NULL;
right = NULL;
}
friend class Stack;
friend class expression_tree;
};
class Stack {
node* head = NULL;
public:
void push(node*);
node* pop();
friend class expression_tree;
};
class expression_tree {
public:
void inorder(node* x)
{
if (x == NULL)
return;
else {
inorder(x->left);
cout << x->value << " ";
inorder(x->right);
}
}
};
void Stack::push(node* x)
{
if (head == NULL) {
head = x;
}
else {
x->next = head;
head = x;
}
}
node* Stack::pop()
{
node* p = head;
head = head->next;
return p;
}
int main()
{
string s = "ABC*+D/";
Stack e;
expression_tree a;
node *x, *y, *z;
int l = s.length();
for (int i = 0; i < l; i++) {
if (s[i] == '+' || s[i] == '-'
|| s[i] == '*' || s[i] == '/'
|| s[i] == '^') {
z = new node(s[i]);
x = e.pop();
y = e.pop();
z->left = y;
z->right = x;
e.push(z);
}
else {
z = new node(s[i]);
e.push(z);
}
}
cout << " The Inorder Traversal of Expression Tree: ";
a.inorder(z);
return 0;
}
|
Output:
The Inorder Traversal of Expression Tree: A + B * C / D
Share your thoughts in the comments
Please Login to comment...