Euclid–Mullin Sequence
Last Updated :
01 Sep, 2022
Given an integer N, the task is to print the first N elements of the Euclid-Mullin Sequence. The Euclid-Mullin sequence is a sequence of prime numbers where each element is the least prime factor of one plus the product of all earlier elements. The sequence is named after the ancient Greek mathematician Euclid. Examples:
Input: N = 14 Output: 2 3 7 43 13 53 5 6221671 38709183810571 139 2801 11 17 5471
Approach: The Euclid–Mullin sequence is a sequence of prime numbers where the nth number of sequence is: 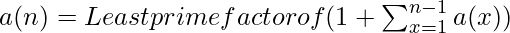 So, we will run a loop from 1 to N and take a variable product which is initially to 1 and will contain the product of all previous elements. We will then find the smallest prime factor of (1 + product) in O(sqrt(n)) time and print the number. Note that the code fails to print numbers after the 14th element as the product becomes too large and finding its smallest prime factor takes a lot of time. Below is the implementation of the above approach:
So, we will run a loop from 1 to N and take a variable product which is initially to 1 and will contain the product of all previous elements. We will then find the smallest prime factor of (1 + product) in O(sqrt(n)) time and print the number. Note that the code fails to print numbers after the 14th element as the product becomes too large and finding its smallest prime factor takes a lot of time. Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
unsigned long long smallestPrimeFactor(unsigned long long n)
{
unsigned long long i = 2;
while ((i * i) <= n)
{
if (n % i == 0)
return i;
i += 1;
}
return n;
}
void solve(unsigned long long n)
{
unsigned long long product = 1;
unsigned long long i = 0;
while (i < n)
{
unsigned long long num = smallestPrimeFactor(product + 1);
cout << num << " ";
product = product * num;
i += 1;
}
}
int main()
{
unsigned long long b = 14;
solve(b);
}
|
Java
import java.math.BigInteger;
class GFG {
static BigInteger smallestPrimeFactor(BigInteger n)
{
BigInteger i = BigInteger.valueOf(2);
while ((i.multiply(i)).compareTo(n) <= 0) {
if (n.mod(i).compareTo(BigInteger.ZERO) == 0)
return i;
i = i.add(BigInteger.ONE);
}
return n;
}
static void solve(BigInteger n)
{
BigInteger product = BigInteger.ONE;
BigInteger i = BigInteger.ZERO;
while (i.compareTo(n) < 0) {
BigInteger num = smallestPrimeFactor(product.add(BigInteger.ONE));
System.out.print(num + " ");
product = product.multiply(num);
i = i.add(BigInteger.ONE);
}
}
public static void main(String[] args)
{
BigInteger b = BigInteger.valueOf(14);
solve(b);
}
}
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static ulong smallestPrimeFactor(ulong n)
{
ulong i = 2;
while ((i * i) <= n)
{
if (n % i == 0)
return i;
i += 1;
}
return n;
}
static void solve(ulong n)
{
ulong product = 1;
ulong i = 0;
while (i < n)
{
ulong num = smallestPrimeFactor(product + 1);
Console.Write(num + " ");
product = product * num;
i += 1;
}
}
public static void Main(string[] args)
{
ulong b = 14;
solve(b);
}
}
|
Python3
def smallestPrimeFactor(n):
i = 2
while (i * i) <= n :
if n % i == 0:
return i
i += 1
return n
def solve(n):
product = 1
i = 0
while i < n:
num = smallestPrimeFactor(product + 1)
print(num, end=' ')
product = product * num
i += 1
b = 14
solve(b)
|
Javascript
function smallestPrimeFactor(n)
{
let i = 2
while ((i * i) <= n)
{
if (n % i == 0)
return i
i += 1
}
return n
}
function solve(n)
{
let product = 1
let i = 0
while (i < n)
{
let num = smallestPrimeFactor(product + 1)
process.stdout.write(num + " ")
product = product * num
i += 1
}
}
let b = 14
solve(b)
|
Output:2 3 7 43 13 53 5 6221671 38709183810571 139 2801 11 17 5471
Time Complexity: O(n*sqrt(n))
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...