Check whether the given number is Euclid Number or not
Last Updated :
20 Feb, 2023
Given a positive integer n, the task is to check if it is Euclid Number or not. Print ‘YES’ if the given number is Euclid Number otherwise print ‘NO’.
Euclid number : In Mathematics, Euclid numbers are integers of the form – 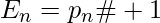
where 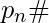 is product of first n prime numbers.
is product of first n prime numbers.
The first few Euclid numbers are-
3, 7, 31, 211, 2311, 30031, 510511, 9699691, ……….
Example:
Input: N = 31
Output: YES
31 can be expressed in the form of
pn# + 1 as p3# + 1
(First 3 prime numbers are 2, 3, 5 and their product is 30 )
Input: N = 43
Output: NO
43 cannot be expressed in the form of pn# + 1
Naive Approach:
- Generate all prime number in the range using Sieve of Eratosthenes.
- Then starting from first prime (i.e 2 ) start multiplying next prime number and keep checking if product + 1 = n .
- If the product + 1 = n then, n is Euclid number. Otherwise not.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define MAX 10000
vector<int> arr;
void SieveOfEratosthenes()
{
bool prime[MAX];
memset(prime, true, sizeof(prime));
for (int p = 2; p * p < MAX; p++) {
if (prime[p] == true) {
for (int i = p * 2; i < MAX; i += p)
prime[i] = false;
}
}
for (int p = 2; p < MAX; p++)
if (prime[p])
arr.push_back(p);
}
bool isEuclid(long n)
{
long long product = 1;
int i = 0;
while (product < n) {
product = product * arr[i];
if (product + 1 == n)
return true;
i++;
}
return false;
}
int main()
{
SieveOfEratosthenes();
long n = 31;
if (isEuclid(n))
cout << "YES\n";
else
cout << "NO\n";
n = 42;
if (isEuclid(n))
cout << "YES\n";
else
cout << "NO\n";
return 0;
}
|
Java
import java.util.*;
class GFG {
static final int MAX = 10000;
static Vector<Integer> arr = new Vector<Integer>();
static void SieveOfEratosthenes()
{
boolean[] prime = new boolean[MAX];
for (int i = 0; i < MAX; i++)
prime[i] = true;
for (int p = 2; p * p < MAX; p++) {
if (prime[p] == true) {
for (int i = p * 2; i < MAX; i += p)
prime[i] = false;
}
}
for (int p = 2; p < MAX; p++)
if (prime[p])
arr.add(p);
}
static boolean isEuclid(long n)
{
long product = 1;
int i = 0;
while (product < n) {
product = product * arr.get(i);
if (product + 1 == n)
return true;
i++;
}
return false;
}
public static void main(String[] args)
{
SieveOfEratosthenes();
long n = 31;
if (isEuclid(n))
System.out.println("YES");
else
System.out.println("NO");
n = 42;
if (isEuclid(n))
System.out.println("YES");
else
System.out.println("NO");
}
}
|
Python3
MAX = 10000
arr = []
def SieveOfEratosthenes():
prime = [True] * MAX
p = 2
while p * p < MAX :
if (prime[p] == True):
for i in range(p * 2, MAX, p):
prime[i] = False
p += 1
for p in range(2, MAX):
if (prime[p]):
arr.append(p)
def isEuclid(n):
product = 1
i = 0
while (product < n) :
product = product * arr[i]
if (product + 1 == n):
return True
i += 1
return False
if __name__ == "__main__":
SieveOfEratosthenes()
n = 31
if (isEuclid(n)):
print("YES")
else:
print("NO")
n = 42
if (isEuclid(n)):
print("YES")
else:
print("NO")
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static readonly int MAX = 10000;
static List<int> arr = new List<int>();
static void SieveOfEratosthenes()
{
bool[] prime = new bool[MAX];
for (int i = 0; i < MAX; i++)
prime[i] = true;
for (int p = 2; p * p < MAX; p++)
{
if (prime[p] == true)
{
for (int i = p * 2; i < MAX; i += p)
prime[i] = false;
}
}
for (int p = 2; p < MAX; p++)
if (prime[p])
arr.Add(p);
}
static bool isEuclid(long n)
{
long product = 1;
int i = 0;
while (product < n)
{
product = product * arr[i];
if (product + 1 == n)
return true;
i++;
}
return false;
}
public static void Main(String[] args)
{
SieveOfEratosthenes();
long n = 31;
if (isEuclid(n))
Console.WriteLine("YES");
else
Console.WriteLine("NO");
n = 42;
if (isEuclid(n))
Console.WriteLine("YES");
else
Console.WriteLine("NO");
}
}
|
Javascript
<script>
var MAX = 10000;
var arr = [];
function SieveOfEratosthenes()
{
var prime = Array(MAX).fill(true);;
for (var p = 2; p * p < MAX; p++) {
if (prime[p] == true) {
for (var i = p * 2; i < MAX; i += p)
prime[i] = false;
}
}
for (var p = 2; p < MAX; p++)
if (prime[p])
arr.push(p);
}
function isEuclid( n)
{
var product = 1;
var i = 0;
while (product < n) {
product = product * arr[i];
if (product + 1 == n)
return true;
i++;
}
return false;
}
SieveOfEratosthenes();
var n = 31;
if (isEuclid(n))
document.write("YES<br>");
else
document.write("NO<br>");
n = 42;
if (isEuclid(n))
document.write("YES<br>");
else
document.write("NO<br>");
</script>
|
Note: Above approach will take O(Pn#) for each query (for every N) i.e. no. of prime numbers to be multiplied to check if n is Euclid number or not.
Auxiliary Space: O(n)
Efficient Approach:
- Generate all prime number in the range using Sieve of Eratosthenes.
- Compute prefix product of prime numbers up to a range to avoid re-calculating the product using hash table.
- If the product + 1 = n then, n is Euclid number. Otherwise not.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
#define MAX 10000
unordered_set<long long int> s;
void SieveOfEratosthenes()
{
bool prime[MAX];
memset(prime, true, sizeof(prime));
for (int p = 2; p * p < MAX; p++) {
if (prime[p] == true) {
for (int i = p * 2; i < MAX; i += p)
prime[i] = false;
}
}
long long int product = 1;
for (int p = 2; p < MAX; p++) {
if (prime[p]) {
product = product * p;
s.insert(product + 1);
}
}
}
bool isEuclid(long n)
{
if (s.find(n) != s.end())
return true;
else
return false;
}
int main()
{
SieveOfEratosthenes();
long n = 31;
if (isEuclid(n))
cout << "YES\n";
else
cout << "NO\n";
n = 42;
if (isEuclid(n))
cout << "YES\n";
else
cout << "NO\n";
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int MAX = 10000;
static HashSet<Integer> s = new HashSet<Integer>();
static void SieveOfEratosthenes()
{
boolean []prime = new boolean[MAX];
Arrays.fill(prime, true);
prime[0] = false;
prime[1] = false;
for (int p = 2; p * p < MAX; p++)
{
if (prime[p] == true)
{
for (int i = p * 2; i < MAX; i += p)
prime[i] = false;
}
}
int product = 1;
for (int p = 2; p < MAX; p++)
{
if (prime[p])
{
product = product * p;
s.add(product + 1);
}
}
}
static boolean isEuclid(int n)
{
if (s.contains(n))
return true;
else
return false;
}
public static void main(String[] args)
{
SieveOfEratosthenes();
int n = 31;
if (isEuclid(n))
System.out.println("Yes");
else
System.out.println("No");
n = 42;
if (isEuclid(n))
System.out.println("Yes");
else
System.out.println("No");
}
}
|
Python3
MAX = 10000
s = set()
def SieveOfEratosthenes():
prime = [True] * (MAX)
prime[0], prime[1] = False, False
for p in range(2, 100):
if prime[p] == True:
for i in range(p * 2, MAX, p):
prime[i] = False
product = 1
for p in range(2, MAX):
if prime[p] == True:
product = product * p
s.add(product + 1)
def isEuclid(n):
if n in s:
return True
else:
return False
if __name__ == "__main__":
SieveOfEratosthenes()
n = 31
if isEuclid(n) == True:
print("YES")
else:
print("NO")
n = 42
if isEuclid(n) == True:
print("YES")
else:
print("NO")
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int MAX = 10000;
static HashSet<int> s = new HashSet<int>();
static void SieveOfEratosthenes()
{
Boolean []prime = new Boolean[MAX];
for (int p = 0; p < MAX; p++)
prime[p] = true;
prime[0] = false;
prime[1] = false;
for (int p = 2; p * p < MAX; p++)
{
if (prime[p] == true)
{
for (int i = p * 2; i < MAX; i += p)
prime[i] = false;
}
}
int product = 1;
for (int p = 2; p < MAX; p++)
{
if (prime[p])
{
product = product * p;
s.Add(product + 1);
}
}
}
static Boolean isEuclid(int n)
{
if (s.Contains(n))
return true;
else
return false;
}
public static void Main(String[] args)
{
SieveOfEratosthenes();
int n = 31;
if (isEuclid(n))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
n = 42;
if (isEuclid(n))
Console.WriteLine("Yes");
else
Console.WriteLine("No");
}
}
|
Javascript
<script>
let MAX = 10000;
let s = new Set();
function SieveOfEratosthenes()
{
let prime = new Array(MAX);
for(let i=0;i<prime.length;i++)
{
prime[i]=true;
}
prime[0] = false;
prime[1] = false;
for (let p = 2; p * p < MAX; p++)
{
if (prime[p] == true)
{
for (let i = p * 2; i < MAX; i += p)
prime[i] = false;
}
}
let product = 1;
for (let p = 2; p < MAX; p++)
{
if (prime[p])
{
product = product * p;
s.add(product + 1);
}
}
}
function isEuclid(n)
{
if (s.has(n))
return true;
else
return false;
}
SieveOfEratosthenes();
let n = 31;
if (isEuclid(n))
document.write("Yes<br>");
else
document.write("No<br>");
n = 42;
if (isEuclid(n))
document.write("Yes<br>");
else
document.write("No<br>");
</script>
|
Note: Above approach will take O(1) time to answer a query.
Share your thoughts in the comments
Please Login to comment...